假設我們現(xiàn)在的需求是實現(xiàn)一個長方形，于是我們寫下了這樣的代碼：
class Rectangle
{
protected double width; protected double height; public double Width
{
set{this.width=value;} get{return this.width;}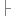
} public double Height { set{this.height=value;} get{return this.height;}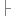 } public double Area//計算長方形的面積 { get{return this.width*this.height;} }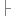
}
這個程序運行得很好，并被安裝到多個Client。但現(xiàn)在需求增加了，Client需要一個正方體Square。按照平面幾何學的觀點，正方形是長與寬相等的特殊的長方形，即Square IS-A Rectangle，于是我們讓Square繼承Rectangle類。（PS:Square繼承了Rectangle后它也有了相應的width和height字段，鑒于Square的長和寬相等，它僅需要這兩個字段中的一個就夠了，這就浪費了內存資源(如果在程序中定義很多個Square對象實例的話)。）
class Square : Rectangle{ public new double Width { set { base.Height = base.Width = value; } get { return base.Width; } }/*由于父類Rectangle在設計時沒有考慮將來會被Square繼承，所以父類中字段width和height都被設成private，在子類Square中就只能調用父類的屬性來set/get。*/ public new double Height { set { base.Width = base.Height = value; } get { return base.Height; } }}
這段代碼貌似運行良好，無論我們對Square和Rectangle對象做任何操作，都與數(shù)學上的正方形和長方形保持一致。這樣看來設計似乎時自相容的、正確的；但是一個自相容的設計未必與所有的用戶程序相容。例如假設我們在定義Square之前，對Rentangle進行了如下的單元測試：
void TestRectangle(Rectangle r){ r.Weight=10; r.Height=20; Assert.AreEqual(10,r.Weight); Assert.AreEqual(200,r.Area);}Rectangle r = new Rectanglt();TestRectangle(r);這段測試代碼運行OK，但現(xiàn)在我們有了Square類，Square IS-A Rectangle，如果我們傳入一個Square對象會如何呢？
Square s = new Square();TestRectangle(s);現(xiàn)在兩個Assert測試都失敗了...這樣看來，Square在某些場合是不能替代Rectangle的，讓Square繼承Rectangle是一種不合理的設計，其違背了Liskov替換原則(LSP)。
(Form《敏捷軟件開發(fā)：原則、模式與實踐》，以下簡稱PPP)LSP讓我們得出一個非常重要的結論：一個模型，如果孤立地看，并不具有真正意義上的有效性，模型的有效性只能通過它的客戶程序來表現(xiàn)。例如孤立地看Rectangle和Squre，它們時自相容的、有效的；但從對基類Rectangle做了合理假設的客戶程序TestRectangle(Rectangle r)看，這個模型就有問題了。在考慮一個特定設計是否恰當時，不能完全孤立地來看這個解決方案，必須要根據(jù)該設計的使用者所作出的合理假設來審視它。
目前也有一些技術可以支持我們將合理假設明確化，例如測試驅動開發(fā)(Test-Driven Development，TDD)和基于契約設計(Design by Contract，DBC)。但是有誰知道設計的使用者會作出什么樣的合理假設呢？大多數(shù)這樣的假設都很難預料。如果我們預測所有的假設的話，我們設計的系統(tǒng)可能也會充滿不必要的復雜性。PPP一書中推薦的做法是：只預測那些最明顯的違反LSP的情況，而推遲對所有其他假設的預測，直到出現(xiàn)相關的脆弱性的臭味(Bad Smell)時，才去處理它們。我覺得這句話還不夠直白，Martin Fowler的《Refactoring》一書中“Refused Bequest”(拒收的遺贈)描述的更詳盡：子類繼承父類的methods和data，但子類僅僅只需要父類的部分Methods或data，而不是全部methods和data；當這種情況出現(xiàn)時，就意味這我們的繼承體系出現(xiàn)了問題。例如上面的Rectangle和Square，Square本身長和寬相等，幾何學中用邊長來表示邊，而Rectangle長和寬之分，直觀地看，Square已經Refused了Rectangle的Bequest，讓Square繼承Rectangle是一個不合理的設計。
現(xiàn)在再回到面向對象的基本概念上，子類繼承父類表達的是一種IS-A關系，IS-A關系這種用法被認為是面向對象分析(OOA)基本技術之一。但正方形的的確確是一個長方形啊，難道它們之間不存在IS-A關系？關于這一點，《Java與模式》一書中的解釋是：我們設計繼承體系時，子類應該是可替代的父類的，是可替代關系，而不僅僅是IS-A的關系；而PPP一書中的解釋是：從行為方式的角度來看，Square不是Rectangle，對象的行為方式才是軟件真正所關注的問題；LSP清楚地指出，OOD中IS-A關系時就行為方式而言的，客戶程序是可以對行為方式進行合理假設的。其實二者表達的是同一個意思。
參考：
《敏捷軟件開發(fā)：原則、模式與實踐》
《Java與模式》
《重構》
浙公網安備 33010602011771號