計量經濟學(十九)——廣義線性模型GLM
廣義線性模型(Generalized Linear Model,GLM)是一種靈活且強大的回歸分析方法,它將傳統線性回歸模型與其他類型的回歸模型整合集成在一起,其核心邏輯就是利用指數族分布的結構,把非線性的響應變量均值問題轉化為一個線性預測問題。GLM 通過指定不同的鏈接函數和分布族,可以適應多種數據類型。它不僅適用于常見的正態分布數據,還能夠處理泊松分布、二項分布、伽馬分布等,適用于計數數據、分類數據和連續數據等。通過選擇合適的鏈接函數(如 log、logit、identity 等)和分布(如泊松分布用于計數數據,二項分布用于分類問題),GLM 能夠為多種回歸問題提供統一框架,且兼容傳統回歸分析方法。

目錄
一、 引言
二、 廣義線性模型(GLM)的基本理論
三、 GLM的估計方法
四、 GLM的診斷
五、 GLM的應用案例
六、 GLM的Python實現
七、 結束語
八、 參考文獻
一、引言
回歸分析在計量經濟學中占據著核心地位,廣泛應用于揭示經濟變量之間的關系。在多元回歸模型的框架下,研究者通過自變量預測因變量。然而,傳統的回歸模型(如線性回歸)假設因變量符合正態分布,且與自變量之間存在線性關系,限制了其應用范圍。在實際經濟問題中,許多情境下因變量并不符合正態分布,且自變量和因變量之間的關系可能是非線性的,這使得傳統的回歸方法無法提供令人滿意的結果。為了解決這些問題,廣義線性模型(GLM)應運而生。
GLM通過引入鏈接函數和適應不同的分布族,擴展了傳統回歸模型的應用范圍,能夠處理如二分類、計數數據、偏態數據等多種復雜情況。本文將詳細探討GLM的理論基礎、主要類型、估計方法、模型診斷以及實際應用,幫助讀者全面理解GLM的內涵及其在計量經濟學中的重要地位。
二、廣義線性模型(GLM)的基本理論
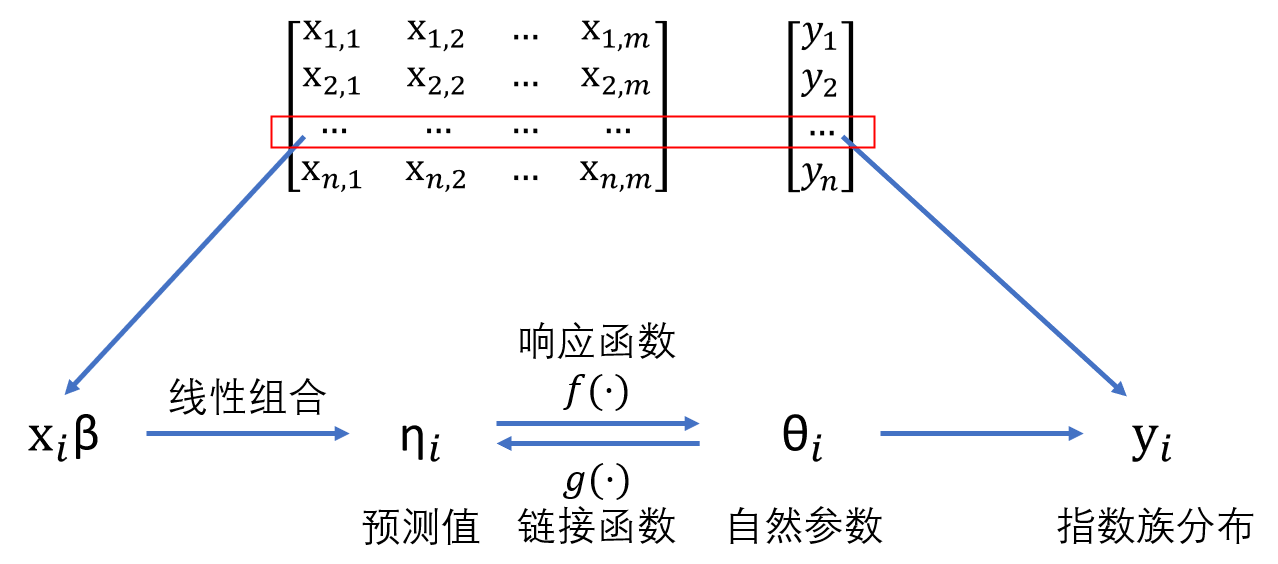
線性回歸的核心思想是響應變量的條件均值可由自變量的線性組合直接刻畫,即\(E[Y \mid X ] = X \beta\)。廣義線性模型(GLM)在此基礎上推廣,引入鏈接函數 \(g (.)\),使得\(g (E[ Y \mid X ]) = X \beta\)。通過這種方式,即使響應變量服從二項分布、泊松分布等非正態分布,也能將均值與線性預測子聯系起來。其底層邏輯是依托于指數族分布,保證了響應變量的均值與自然參數之間存在可逆函數關系,而線性預測子 \(X \beta\) 則為建模提供了穩定而統一的框架。
廣義線性模型(GLM)是一類靈活的回歸模型,它通過引入不同的概率分布和鏈接函數,適應了多種類型的響應變量,克服了傳統回歸模型的局限性。GLM的框架由三部分組成:隨機成分、系統成分和鏈接函數。廣義線性模型的數學表示為:
其中:
- $ \mu = E(Y)$ 是響應變量\(Y\) 的期望值。
- \(g(\mu)\) 是鏈接函數。
- \(\eta = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p\)是系統成分,即自變量與回歸系數的線性組合。
這個公式展示了如何通過鏈接函數 $ g(\mu)$將響應變量的期望值與自變量之間的線性關系連接起來。下面將詳細介紹這三個成分:隨機成分、系統成分和鏈接函數。
2.1 隨機成分(Random Component)
隨機成分描述了響應變量的分布情況。在GLM中,響應變量 \(Y\) 通常假設服從某個指數分布族(如正態分布、二項分布、泊松分布等)。這些分布族描述了響應變量如何受到隨機因素的影響,并影響其分布形式。具體來說,響應變量 \(Y\) 的概率密度函數可以表示為:
其中:
- \(\theta\) 是分布的自然參數。
- $ b(\theta)$ 和 $ c(y, \phi)$ 是由具體分布形式決定的函數。
- \(\phi\) 是尺度參數。
常見的分布族包括:
- 正態分布:用于處理連續數據,如股市價格、收入等。
- 二項分布:用于處理二分類數據,如是否患病、是否購買某產品等。
- 泊松分布:用于處理計數數據,如事故發生次數、客戶到店數量等。
- Gamma分布:常用于處理正偏態數據,如保險賠付金額、排隊時間等。
2.2 系統成分(Systematic Component)
系統成分描述了自變量與響應變量之間的線性關系。這個部分由自變量和回歸系數組成,通常表示為:
其中:
- $ \eta $ 是線性預測量(即自變量的加權和)。
- \(X_1, X_2, \dots, X_p\) 是自變量。
- \(\beta_0, \beta_1, \dots, \beta_p\) 是回歸系數。
系統成分通常用于建立自變量與響應變量之間的線性關系,但需要通過鏈接函數與響應變量的期望值(\(\mu\))建立聯系。
2.3 鏈接函數(Link Function)
鏈接函數將系統成分(線性預測量)與響應變量的期望值 \(\mu = E(Y)\) 聯系起來。不同類型的響應變量需要不同的鏈接函數。鏈接函數的作用是將響應變量的期望值與自變量的線性組合進行非線性變換,常見的鏈接函數包括:
- 對數鏈接函數(用于泊松回歸、Gamma回歸等):\(g(\mu) = \log(\mu)\)
- 邏輯斯蒂鏈接函數(用于邏輯回歸):\(g(\mu) = \log \left( \frac{\mu}{1 - \mu} \right)\)
- 恒等鏈接函數(用于線性回歸):$g(\mu) = \mu $
通過這些鏈接函數,GLM能夠處理自變量與響應變量之間的非線性關系,從而適應更多復雜的回歸問題。
2.4 GLM的常見特例
廣義線性模型(GLM)是一個通用框架,可以根據響應變量的類型和分布選擇不同的特例。下面列舉十種常見的GLM特例:
| 模型類型 | 響應變量分布 | 鏈接函數 | 應用場景 |
|---|---|---|---|
| 多元線性回歸(Multiple Linear Regression) | 正態分布 | 恒等函數 \(g(\mu) = \mu\) | 預測連續型經濟指標,如收入、GDP、股價等 |
| 邏輯回歸(Logistic Regression) | 二項分布 | 邏輯斯蒂函數 \(g(\mu) = \log\frac{\mu}{1-\mu}\) | 二分類問題,如信用違約預測、患病概率預測 |
| 泊松回歸(Poisson Regression) | 泊松分布 | 對數函數 \(g(\mu) = \log(\mu)\) | 計數數據分析,如事故次數、客戶到店次數 |
| 負二項回歸(Negative Binomial Regression) | 負二項分布 | 對數函數\(g(\mu) = \log(\mu)\) | 過度離散的計數數據,如保險理賠次數、疾病發病次數 |
| Gamma回歸(Gamma Regression) | Gamma分布 | 對數函數\(g(\mu) = \log(\mu)\) | 處理正偏態連續數據,如保險賠付金額、排隊時間 |
| 多項Logit回歸(Multinomial Logistic Regression) | 多項分布 | 對數幾率函數 \(g(\mu_i) = \log\frac{\mu_i}{\mu_J}\) | 多分類問題,如消費者購買品牌選擇、投票意向預測 |
| Ordinal Logit回歸(Ordinal Logistic Regression) | 有序多項分布 | 對數幾率函數 \(g(\mu_i) = \log\frac{P(Y \le i)}{P(Y > i)}\) | 有序分類問題,如滿意度評分(差、中、好) |
| Probit回歸(Probit Regression) | 二項分布 | 普通正態函數 \(g(\mu) = \Phi^{-1}(\mu)\) | 二分類問題,類似邏輯回歸,常用于金融、醫學等領域 |
| Beta回歸(Beta Regression) | Beta分布 | 對數it函數 \(g(\mu) = \log\frac{\mu}{1-\mu}\) | 處理比例數據,如市場份額、轉化率、占比數據 |
| Quasi-Poisson回歸(Quasi-Poisson Regression) | 近似泊松分布 | 對數函數\(g(\mu) = \log(\mu)\) | 處理過度離散計數數據,但不嚴格假設泊松分布 |
上述結構展示了GLM的通用數學表達式,依次解釋了三個組成部分——隨機成分、系統成分和鏈接函數,并給出了每一部分的具體數學表達和應用場景。這使得讀者可以更好地理解廣義線性模型的構建和應用。
泊松分布與 GLM
- 分布形式:
\[P(Y=y) = \frac{e^{-\mu}\mu^y}{y!}, \quad y=0,1,2,\dots \]- 指數族改寫:
\[P(Y=y) = \exp\left(y \log \mu - \mu - \log y!\right) \]可得自然參數 \(\theta = \log \mu\)。- 均值關系:
\[\mathbb{E}[Y] = e^{\theta} = \mu \]
- GLM 表達:
\[\log \mu = X\beta \quad \Rightarrow \quad \mu = e^{X\beta} \]泊松分布屬于指數族,GLM 使用 對數鏈接函數 將均值建模為自變量的線性函數。
三、GLM的估計方法
廣義線性模型(GLM)的核心任務是估計回歸系數 \(\beta = (\beta_0, \beta_1, \dots, \beta_p)^\top\),從而刻畫自變量與響應變量之間的關系。與傳統線性回歸不同,GLM允許響應變量服從非正態分布,這使得最小二乘法不再適用。因此,GLM的參數估計通常依賴于最大似然估計(MLE),結合數值優化方法如迭代加權最小二乘法(IWLS)來實現。
3.1 最大似然估計(MLE)
最大似然估計是一種通用且有效的參數估計方法,其核心思想是選擇一組參數,使得在該參數下觀測數據出現的概率(即似然函數)最大。對于GLM,假設響應變量 \(Y_i\) 獨立且服從指數分布族,其概率密度函數可表示為:
其中,\(\theta_i\) 是自然參數,\(\phi\) 是尺度參數。最大化似然函數 \(L(\beta) = \prod_{i=1}^n f_Y(y_i|\theta_i(\beta))\) 等價于最大化對數似然函數:
通過對 \(\beta\) 求導并令其導數為零,可以得到最大似然方程。然而,由于許多GLM模型的對數似然方程是非線性的,解析解往往不存在,因此需要數值迭代方法求解。
3.2 迭代加權最小二乘法(IWLS)
迭代加權最小二乘法(IWLS)是GLM中求解最大似然估計的標準算法。其基本思想是將非線性的最大似然估計問題轉化為一系列加權最小二乘問題,通過不斷迭代更新回歸系數,直到收斂。具體步驟如下:
- 初始化回歸系數 \(\beta^{(0)}\)。
- 計算當前系數下的線性預測量 \(\eta^{(t)} = X \beta^{(t)}\) 及響應變量的期望值 \(\mu^{(t)} = g^{-1}(\eta^{(t)})\)。
- 構造權重矩陣 \(W^{(t)}\) 和調整響應變量的偽響應 \(z^{(t)}\):\[z^{(t)} = \eta^{(t)} + (y - \mu^{(t)}) \left( \frac{d\eta}{d\mu} \right)_{\mu^{(t)}} \]
- 求解加權最小二乘方程:\[\beta^{(t+1)} = (X^\top W^{(t)} X)^{-1} X^\top W^{(t)} z^{(t)} \]
- 重復步驟2-4,直到 \(\beta\) 收斂(變化量小于設定閾值)。
IWLS方法能夠高效處理各種分布族和鏈接函數,使得GLM的參數估計過程在理論上嚴謹且在計算上可行。通過MLE與IWLS,研究者可以在不同類型的數據下得到穩健的回歸系數,從而對經濟變量之間的關系進行有效建模與推斷。|
四、GLM的診斷
在廣義線性模型(GLM)建模過程中,診斷分析是確保模型有效性和穩健性的重要環節。由于GLM允許響應變量服從非正態分布,模型可能存在擬合不足、異常值或系統性偏差,因此對殘差、擬合優度和偏差進行檢查,有助于發現潛在問題并優化模型結構。
4.1 殘差分析
殘差分析用于檢查模型擬合效果和數據的異常情況。在GLM中,常用殘差類型包括偏差殘差(deviance residuals)、皮爾遜殘差(Pearson residuals)和工作殘差(working residuals)。偏差殘差定義為:
其中,\(\ell(\cdot)\)為對數似然函數,\(\hat{\mu}_i\)為模型預測值。通過繪制殘差與擬合值的散點圖,可以發現異常值、非線性趨勢或異方差問題,從而判斷模型是否需要調整或引入其他變量。
4.2 擬合優度檢驗
擬合優度檢驗用于評估模型解釋響應變量的能力。常用的方法包括:
- 卡方檢驗(Chi-square test):對比模型殘差與理論分布,判斷模型是否合理。
- 赤池信息準則(AIC, Akaike Information Criterion):
其中,\(\ell(\hat{\beta})\)是對數似然值,\(k\)是模型參數個數。AIC值越小,模型擬合越優。
- 貝葉斯信息準則(BIC, Bayesian Information Criterion):
BIC在模型選擇中考慮了樣本量,適用于比較不同復雜度的模型。
這些指標可以幫助研究者在多個候選模型中選擇最優模型,并避免過擬合。
4.3 偏差診斷
偏差診斷用于檢查模型是否存在系統性誤差,即模型假設與數據實際分布的偏離情況。常用方法包括偏差殘差圖和偏差分布圖。通過分析殘差分布是否接近零均值及是否存在規律性偏差,可以判斷模型是否遺漏重要變量或選擇了不合適的鏈接函數。如果發現明顯模式,則可能需要重新定義自變量或選擇更合適的分布族。
綜合來看,GLM的診斷環節對于保證模型的穩健性和預測能力至關重要。通過殘差分析、擬合優度檢驗和偏差診斷,研究者不僅可以發現異常數據和潛在問題,還能夠進一步優化模型結構,提高對經濟、金融及社會科學數據的解釋力和預測精度。
五、GLM的應用案例
廣義線性模型(GLM)因其靈活性和適用性,在各行各業的數據分析中都有廣泛應用。它不僅可以處理連續型響應變量,還能對二分類、多分類以及計數型數據進行建模,因此在醫療、金融和社會科學等領域都表現出重要價值。
5.1 醫療數據分析
在醫療領域,GLM被廣泛應用于疾病預測、風險評估和醫療資源規劃。舉例來說,邏輯回歸可用于預測患者是否患有某種慢性疾病,如糖尿病或心血管疾病。研究者可以將年齡、性別、血壓、血糖水平、生活習慣等作為自變量,構建邏輯回歸模型,從而估計每位患者的患病概率。此外,泊松回歸則常用于預測患者的住院次數或急診就診次數。通過將患者的歷史就診記錄、病情嚴重程度和治療方案作為自變量,泊松回歸能夠合理地模擬計數型響應變量,為醫院資源配置提供決策依據。GLM在醫療數據分析中不僅能夠提高預測精度,還能幫助識別重要的風險因素,為公共衛生政策制定提供科學依據。
5.2 金融數據分析
在金融領域,GLM同樣有著廣泛應用,尤其在信用風險管理和保險精算中發揮重要作用。例如,泊松回歸可以用來預測保險理賠的次數,通過分析客戶的年齡、性別、職業、投保類型和歷史理賠記錄,模型可以為保險公司提供合理的賠付預測。另一方面,邏輯回歸則是信用評分模型的核心工具,用于預測客戶是否會違約。通過將客戶的收入水平、信用歷史、負債比率等作為自變量,邏輯回歸能夠估計違約概率,為信貸審批和風險控制提供數據支持。GLM在金融數據分析中,能夠處理二分類與計數型問題,使金融機構在風險管理和精算定價方面更加科學和精準。
5.3 社會科學研究
在社會科學領域,GLM被廣泛用于教育、社會行為、政治投票及公共政策研究。例如,邏輯回歸可以用于分析選民是否會支持某一政策或候選人,將性別、年齡、收入水平、教育背景等因素作為自變量,預測選民行為概率。泊松回歸則可用于研究事件發生頻率,如青少年犯罪率、參與志愿活動的次數等。GLM的應用不僅可以幫助研究人員理解社會現象背后的因果關系,還可以通過模型解釋變量的重要性,為政策制定和社會干預提供量化依據。此外,GLM能夠適應不同類型的響應變量,使得社會科學研究者能夠處理從連續到計數、從二分類到多分類的多樣化數據問題。
廣義線性模型在各個領域都體現出強大的建模能力和實用價值,通過選擇合適的分布和鏈接函數,研究人員和決策者能夠針對不同數據類型進行科學建模,實現對復雜現實問題的精準分析和預測。
六、GLM的Python實現
6.1 廣義線性模型的擬合函數
Python中sm.GLM() 方法來擬合不同類型的廣義線性模型,并且指明了每個模型對應的 family 和 link。
| 模型類型 | GLM 用法示例 | family 設置 | link 函數設置 | 備注 |
|---|---|---|---|---|
| 多元線性回歸(Multiple Linear Regression) | sm.GLM(y, X, family=sm.families.Gaussian(), link=sm.families.links.identity()) | Gaussian | 恒等函數(identity) | 適用于連續型響應變量,預測經濟指標等 |
| 邏輯回歸(Logistic Regression) | sm.GLM(y, X, family=sm.families.Binomial(), link=sm.families.links.logit()) | Binomial | 邏輯斯蒂函數(logit) | 用于二分類問題,如信用違約預測、患病概率預測等 |
| 泊松回歸(Poisson Regression) | sm.GLM(y, X, family=sm.families.Poisson(), link=sm.families.links.log()) | Poisson | 對數函數(log) | 適用于計數數據分析,如事故次數、客戶到店次數等 |
| 負二項回歸(Negative Binomial Regression) | sm.GLM(y, X, family=sm.families.NegativeBinomial(), link=sm.families.links.log()) | NegativeBinomial | 對數函數(log) | 適用于過度離散的計數數據,如保險理賠次數、疾病發病次數等 |
| Gamma回歸(Gamma Regression) | sm.GLM(y, X, family=sm.families.Gamma(), link=sm.families.links.log()) | Gamma | 對數函數(log) | 適用于處理正偏態連續數據,如保險賠付金額、排隊時間等 |
| 多項Logit回歸(Multinomial Logistic Regression) | sm.GLM(y, X, family=sm.families.Multinomial(), link=sm.families.links.logit()) | Multinomial | 對數幾率函數(logit) | 適用于多分類問題,如消費者購買品牌選擇、投票意向預測等 |
| Ordinal Logit回歸(Ordinal Logistic Regression) | sm.GLM(y, X, family=sm.families.Binomial(), link=sm.families.links.logit()) | Ordinal(可選) | 對數幾率函數(logit) | 用于有序分類問題,如滿意度評分、等級評分等 |
| Probit回歸(Probit Regression) | sm.GLM(y, X, family=sm.families.Binomial(), link=sm.families.links.probit()) | Binomial | 普通正態函數(probit) | 適用于二分類問題,通常與Logit回歸進行比較 |
| Beta回歸(Beta Regression) | sm.GLM(y, X, family=sm.families.Beta(), link=sm.families.links.logit()) | Beta | 對數it函數(logit) | 處理比例數據,如市場份額、轉化率、占比數據等 |
| Quasi-Poisson回歸(Quasi-Poisson Regression) | sm.GLM(y, X, family=sm.families.Poisson(), link=sm.families.links.log()) | Poisson | 對數函數(log) | 用于過度離散計數數據,但不嚴格假設泊松分布 |
說明:
- family:指定響應變量的分布類型。
- link:指定鏈接函數,它定義了響應變量與線性預測器之間的關系。例如,Logit 函數是針對二分類的邏輯回歸,Log 函數是泊松回歸、負二項回歸、Gamma回歸的常用鏈接函數。
6.2 Python程序
Seaborn 提供了一個內置的 penguins 數據集,用于分析不同企鵝物種的特征與分布。該數據集包含多個生物學特征,如 bill_length_mm(喙長)、bill_depth_mm(喙深)、flipper_length_mm(鰭長)等,以及不同物種的標簽。我們可以通過這些數據來建立回歸模型,探索企鵝物種特征與其分布之間的關系,進而分析不同特征對物種分布的影響。
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.genmod.families import Poisson
from statsmodels.genmod.families.links import log
import seaborn as sns
import matplotlib.pyplot as plt
# 加載 seaborn 自帶的 'penguins' 數據集
data = sns.load_dataset('penguins')
# 查看數據
print(data.head())
# 過濾缺失數據
data_cleaned = data.dropna(subset=['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'species'])
# 顯示清洗后的數據
print(data_cleaned.head())
# 將品種 'species' 轉換為分類變量,并轉換為整數編碼
data_cleaned['species_code'] = data_cleaned['species'].astype('category').cat.codes
# 定義自變量和因變量
X = data_cleaned[['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm']] # 多個自變量
X = sm.add_constant(X) # 添加常數項
y = data_cleaned['species_code'] # 因變量:品種的編碼(0, 1, 2)
# GLM建模:Poisson回歸
poisson_model = sm.GLM(y, X, family=Poisson(), link=log())
poisson_results = poisson_model.fit()
# 輸出回歸結果
print(poisson_results.summary())
# 輸出預測的品種編碼
y_pred = poisson_results.predict(X)
# 可視化結果:通過散點圖和預測值
plt.figure(figsize=(10, 6))
# 使用不同顏色展示預測和實際物種
sns.scatterplot(x=y, y=y_pred, color='blue', alpha=0.6)
# 添加標簽和標題
plt.xlabel('True Species Code')
plt.ylabel('Predicted Species Code')
plt.title('True vs Predicted Species Code')
# 顯示圖表
plt.show()
# 可選:使用分類的色彩顯示
sns.scatterplot(x=y, y=y_pred, hue=y, palette="deep", alpha=0.6)
# 再次設置標簽和標題
plt.xlabel('True Species Code')
plt.ylabel('Predicted Species Code')
plt.title('True vs Predicted Species Code with Classification')
plt.legend(title='Species')
plt.show()

species island bill_length_mm ... flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 ... 181.0 3750.0 Male
1 Adelie Torgersen 39.5 ... 186.0 3800.0 Female
2 Adelie Torgersen 40.3 ... 195.0 3250.0 Female
3 Adelie Torgersen NaN ... NaN NaN NaN
4 Adelie Torgersen 36.7 ... 193.0 3450.0 Female
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: species_code No. Observations: 342
Model: GLM Df Residuals: 338
Model Family: Poisson Df Model: 3
Link Function: Log Scale: 1.0000
Method: IRLS Log-Likelihood: -277.76
Date: Sat, 06 Sep 2025 Deviance: 98.035
Time: 16:07:10 Pearson chi2: 80.7
No. Iterations: 5 Pseudo R-squ. (CS): 0.5799
Covariance Type: nonrobust
=====================================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------------
const -2.6067 1.491 -1.748 0.080 -5.530 0.316
bill_length_mm 0.1349 0.018 7.606 0.000 0.100 0.170
bill_depth_mm -0.3259 0.042 -7.797 0.000 -0.408 -0.244
flipper_length_mm 0.0079 0.007 1.168 0.243 -0.005 0.021
=====================================================================================
6.3 結果分析
這是通過 廣義線性模型 (GLM) 使用泊松回歸模型對企鵝物種分布進行分析的結果。模型使用 log 鏈接函數,目的是預測不同企鵝物種(用 species_code 表示)在不同生物學特征下的出現頻率。
模型參數解讀
-
截距項 (
const):
截距為 -2.6067,表示當所有自變量(如喙長、喙深、鰭長)均為 0 時,企鵝物種的出現頻率的對數值。由于 p 值為 0.080(略大于 0.05),這表明截距項的統計顯著性不強,但仍然接近于顯著性水平。 -
bill_length_mm(喙長):
系數為 0.1349,表示喙長每增加 1 毫米,企鵝物種出現頻率的對數值增加 0.1349。這個系數的 p 值為 0.000,遠小于 0.05,表明喙長在模型中對物種分布有顯著影響。 -
bill_depth_mm(喙深):
系數為 -0.3259,表示喙深每增加 1 毫米,企鵝物種出現頻率的對數值減少 0.3259。p 值為 0.000,表明喙深對物種分布有顯著負向影響。 -
flipper_length_mm(鰭長):
系數為 0.0079,表示鰭長每增加 1 毫米,企鵝物種出現頻率的對數值增加 0.0079。p 值為 0.243,表明鰭長對物種分布的影響不顯著。
模型評估
- 對數似然值 (
Log-Likelihood):
-277.76,表明模型擬合的好壞,較低的對數似然值通常意味著模型擬合不夠好。 - 偏差(Deviance):
98.035,偏差越小,模型的擬合越好。在泊松回歸中,偏差可以用來衡量模型的擬合度,較低的偏差通常代表更好的模型擬合。 - 皮爾遜卡方(Pearson chi2):
80.7,用于評估模型擬合的好壞,較低的卡方值表示模型的擬合較好。 - 偽 R2 (Pseudo R-squared):
偽 R2 值為 0.5799,表示模型解釋了約 57.99% 的物種分布的變化,表明該模型具有較好的擬合效果。
顯著性檢驗
- 喙長 (bill_length_mm) 和 喙深 (bill_depth_mm) 都具有顯著影響(p < 0.05),這兩個變量與物種分布具有顯著的正向和負向相關關系。
- 鰭長 (flipper_length_mm) 的 p 值為 0.243,大于 0.05,表示鰭長在模型中的影響不顯著。
最終模型
根據上述分析,最終的廣義線性模型公式為:
log(species_code) = -2.6067 + 0.1349 * bill_length_mm - 0.3259 * bill_depth_mm} + 0.0079 * flipper_length_mm
其中:
- species_code:企鵝物種的出現頻率。
- bill_length_mm:喙長(單位:毫米)。
- bill_depth_mm:喙深(單位:毫米)。
- flipper_length_mm:鰭長(單位:毫米)。
結論
- 喙長和喙深對企鵝物種的分布有顯著影響。喙長越長,物種出現頻率越高;而喙深越大,物種出現頻率越低。
- 鰭長在該模型中對物種分布的影響不顯著,因此可以考慮在進一步建模時去除該變量。
- 該模型解釋了約 57.99% 的企鵝物種分布變異,表現出較好的擬合度。
七、結束語
廣義線性模型(GLM)作為多元線性回歸的自然擴展,提供了一個統一而靈活的框架,使研究者能夠處理各種類型的響應變量,包括連續、二分類、多分類及計數型數據。通過引入不同的概率分布和鏈接函數,GLM克服了傳統線性回歸在非正態數據、異方差或非線性關系下的局限性。本文從GLM的基本理論出發,詳細介紹了隨機成分、系統成分和鏈接函數的數學表達,并結合最大似然估計和迭代加權最小二乘法解釋了參數估計方法。在應用層面,GLM在醫療、金融和社會科學等領域展現了重要價值,無論是疾病預測、信用評分,還是社會行為建模,都體現了其靈活性和高效性。未來,隨著數據量和數據類型的不斷增加,GLM及其擴展模型將在經濟、社會和工程領域的決策分析中發揮更大的作用,成為計量經濟學、金融學和社會科學數據分析的重要工具。
參考文獻
- McCullagh, P., & Nelder, J. A. (1989). Generalized Linear Models. 2nd Edition. Chapman & Hall/CRC.
- Agresti, A. (2015). Foundations of Linear and Generalized Linear Models. 2nd Edition. Wiley.
- Dobson, A. J., & Barnett, A. (2018). An Introduction to Generalized Linear Models. 4th Edition. CRC Press.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. 2nd Edition. Springer.
- Cameron, A. C., & Trivedi, P. K. (2013). Regression Analysis of Count Data. 2nd Edition. Cambridge University Press.



 浙公網安備 33010602011771號
浙公網安備 33010602011771號