[LeetCode] 1361. Validate Binary Tree Nodes 驗證二叉樹

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

Example 1:

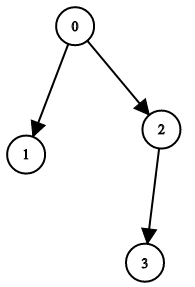
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

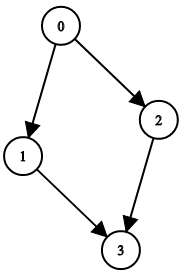
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

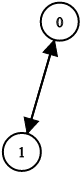
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Constraints:

n == leftChild.length == rightChild.length
1 <= n <= 104
-1 <= leftChild[i], rightChild[i] <= n - 1

這道題說是給了兩個數組 leftChild 和 rightChild，其中 leftChild[i] 表示結點i的左子結點，rightChild[i] 表示結點i的右子結點，若值為 -1，表示沒有左子結點或著右子結點，問給定的數組是否可以組成一個有效的二叉樹。對于二叉樹想必大家都不陌生，來看一下題目中給的例子，例子1是一棵有效的二叉樹，例子2中由于結點3有兩個父結點，所以不是有效的二叉樹，例子3中兩個結點互為父結點了，這也不是有效的二叉樹。二叉樹是一種特殊的有向圖，一棵有效的二叉樹至少要具備這個幾個特點，首先是只有一個根結點，即所有結點必須是連成一個整體的，其次是每個結點最多有兩個子結點，然后每個結點最多只有一個父結點，最后就是不能出現環。

有向圖有個入度 In Degree 的概念，就是某個結點被其他結點連通的個數，對于有效二叉樹來說，除了根結點之外的每個結點的入度必須是1，即每個結點最多只有一個父結點，根結點的入度是0，其沒有父結點。那這里就可以通過計算每個結點的入度，來快速去除一些無效的二叉樹，這里用個長度為n的入度數組 inDegree，然后遍歷兩個數組，若左子結點不為 -1，則將其入度值自增1，此時判斷一下，若入度值大于1了，說明是無效的二叉樹，返回 false，對右子結點進行相同的處理。

僅判斷結點的入度值是不夠的，比如例子3中，每個結點的入度都是1，但不是有效二叉樹，因為其沒有根結點，所以接下來需要找出根結點，而且只能有一個根結點，就是說只能有一個結點的入度是0，若找到了多個，則返回 false。找到了根結點后也還不能說就是有效的二叉函數了，還得保證所有的結點都是相連的，這個通過從根結點開始遍歷二叉樹，統計遍歷到的結點個數，若成功遍歷了n個結點，才能說是有效的二叉樹。遍歷的方法可以用 BFS 或者 DFS，這里先用 BFS，使用隊列 queue 來輔助運算，先把根結點 root 放進去，然后進行 while 循環，每次從 queue 中取出一個結點，計數器 cnt 自增1，然后看其左右子結點，若存在就加入到隊列中繼續循環，最后判斷 cnt 是否等于n即可，參見代碼如下：

解法一：

class Solution {
public:
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        int root = -1, cnt = 0;
        vector<int> inDegree(n);
        for (int i = 0; i < n; ++i) {
            int left = leftChild[i], right = rightChild[i];
            if (left != -1 && ++inDegree[left] > 1) return false;
            if (right != -1 && ++inDegree[right] > 1) return false;
        }
        for (int i = 0; i < n; ++i) {
            if (inDegree[i] != 0) continue;
            if (root != -1) return false;
            root = i;
        }
        if (root == -1) return false;
        queue<int> q{{root}};
        while (!q.empty()) {
            auto t = q.front(); q.pop();
            ++cnt;
            if (leftChild[t] != -1) q.push(leftChild[t]);
            if (rightChild[t] != -1) q.push(rightChild[t]);
        }
        return cnt == n;
    }
};

下面解法是用 DFS 來遍歷二叉樹，寫起來更加簡潔一些，在遞歸函數中首先判斷若當前結點 node 為 -1，說明不存在，則返回0，否則分別對其左右子結點調用遞歸函數，將返回值加起來，再加上1，就是以當前結點 node 為根結點的二叉樹的結點個數了，參見代碼如下：

解法二：

class Solution {
public:
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        int root = -1, cnt = 0;
        vector<int> inDegree(n);
        for (int i = 0; i < n; ++i) {
            int left = leftChild[i], right = rightChild[i];
            if (left != -1 && ++inDegree[left] > 1) return false;
            if (right != -1 && ++inDegree[right] > 1) return false;
        }
        for (int i = 0; i < n; ++i) {
            if (inDegree[i] != 0) continue;
            if (root != -1) return false;
            root = i;
        }
        if (root == -1) return false;
        return countNodes(leftChild, rightChild, root) == n;
    }
    int countNodes(vector<int>& leftChild, vector<int>& rightChild, int node) {
        if (node == -1) return 0;
        return 1 + countNodes(leftChild, rightChild, leftChild[node]) + countNodes(leftChild, rightChild, rightChild[node]);
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1361

參考資料：

https://leetcode.com/problems/validate-binary-tree-nodes/

https://leetcode.com/problems/validate-binary-tree-nodes/solutions/517557/c-find-root-dfs/

LeetCode All in One 題目講解匯總(持續更新中...)