[LeetCode] 1335. Minimum Difficulty of a Job Schedule 工作計劃的最低難度

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.

You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

Example 1:

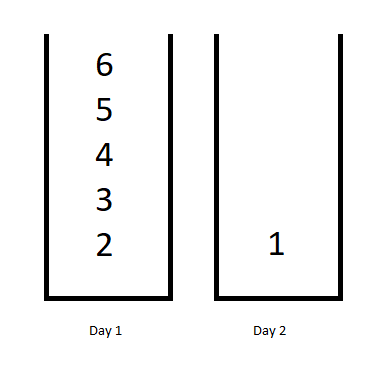
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

Constraints:

1 <= jobDifficulty.length <= 300
0 <= jobDifficulty[i] <= 1000
1 <= d <= 10

這道題說是需要在d天內安排一些工作，且說明各項工作要按照順序做，給定了每項工作的難度，放在數組 jobDifficulty 中。現在說是每天至少要完成一項工作，定義整個工作安排的難度為每天的難度之和，而每天的難度為當前最難的那項工作的難度，現在讓返回d天的最小工作安排的難度。通過分析題目中給定的例子不難理解題意，其中例子2是一種 corner case，即若工作的個數小于天數的話是沒法安排的，因為題目中限定了每天至少做一項工作。為了找出題目的本質考查點，需要褪去背景設定，這道題的本質就是要將給定的數組 jobDifficulty 分為d個子數組，然后將每個子數組中的最大值加起來，使得這個總和最小。看穿了本質之后，就要來考慮如何解題了，對于這種玩數組求極值的題目，基本上動態規劃 Dynamic Programming 就是不二之選了。

首先來考慮下 DP 數組如何定義，這里的主要信息就是天數和工作數，可以用一個二維數組，其中 dp[i][j] 表示當前安排到第 ith 天（0開頭的），且最后一個工作安排到第 jth 個工作，此時的最小難度。將 dp 數組初始化為整型最大值，將 dp[0][0] 初始化為0，因為此時安排到第0天，且唯一安排到的工作就是第0個工作（注意這里計數是從0開始的），則難度就是該工作的難度值 jobDifficulty[0]。接下來需要更新所有的 dp[0][j]，因為當前只安排了一天工作，那么不論最后安排到哪個工作，都應該在一天內完成，則難度是 [0, j] 范圍內的最大值。于是可以用 dp[0][j-1] 和 jobDifficulty[j] 中的較大值來更新 dp[0][j]。

接下來求狀態轉移方程，對于任意的 dp[i][j] 來說，此時安排到第 ith 天，且最后安排到的工作為第 jth 個，此時區間 [0, j] 內的工作都已經安排過了，對于今天做了多少工作我們不確定，但是可以遍歷今天可以安排工作的所有情況，比如今天可能只安排了第 jth 個工作，那么今天的 dp 值就應該是 dp[i-1][j-1] + jobDifficulty[j] 了，因為前一天工作安排到第 j-1 個工作，加上工作j的難度就是今天 dp 值了。但是今天也可以安排多個工作，比如今天可以安排 [i, j] 中若干個工作（即從工作j開始往前直到工作i），不能安排第 ith 個工作之前第工作，因為要保證之前每天至少安排了一個工作，也不能大于第 jth 個工作，因為這是今天能安排到的最后一個工作。需要遍歷所有的情況，同時找出該區間段的最大值 curMax，加到前一個 dp 值上，于是可以用 dp[i-1][k-1] + curMax 來更新 dp[i][j]，最終的結果保存在 dp[d-1][n-1] 中返回即可，參見代碼如下：

解法一：

class Solution {
public:
    int minDifficulty(vector<int>& jobDifficulty, int d) {
        int n = jobDifficulty.size();
        if (d > n) return -1;
        vector<vector<int>> dp(d, vector<int>(n, INT_MAX));
        dp[0][0] = jobDifficulty[0];
        for (int j = 1; j < n; ++j) {
            dp[0][j] = max(dp[0][j - 1], jobDifficulty[j]);
        }
        for (int i = 1; i < d; ++i) {
            for (int j = i; j < n; ++j) {
                int curMax = jobDifficulty[j];
                for (int k = j; k >= i; --k) {
                    curMax = max(curMax, jobDifficulty[k]);
                    dp[i][j] = min(dp[i][j], dp[i - 1][k - 1] + curMax);
                }
            }
        }
        return dp[d - 1][n - 1];
    }
};

我們也可以使用遞歸加記憶數組的方式來做，這里為了遞歸方便，將 memo 數組大小定為 d+1 by n，均初始化為 -1。在遞歸函數中，首先是一系列的終止條件判斷，若 dayLeft 為0了，且 idx 為n了，則返回0，表示此時沒有工作需要安排，所以難度為0。否則若 dayLeft 為0，或者 idx 為0，說明此時狀態不合法，不能成功的安排工作，返回整型最大值。否則若當前狀態 memo[dayLeft][idx] 不為-1，說明當前狀態之前計算過了，直接返回 memo 中的值即可。否則就要進行計算了，定義 curMax 為工作 idx 的難度，核心思想跟上面的 dp 方法基本相同，i從 idx 遍歷到n，更新當前范圍內的最大值 curMax，表示今天安排 [idx, i] 范圍內的所有工作，然后調用遞歸函數，參數傳入 dayLeft-1 和 i+1，判斷若返回值不等于整型最大值 INT_MAX，說明可以成功安排，用其返回值更新最終結果 res，最后將當前狀態 memo[dayLeft][idx] 賦值為 res 并返回即可，參見代碼如下：

解法二：

class Solution {
public:
    int minDifficulty(vector<int>& jobDifficulty, int d) {
        int n = jobDifficulty.size();
        if (d > n) return -1;
        vector<vector<int>> memo(d + 1, vector<int>(n, -1));
        return dfs(jobDifficulty, d, 0, memo);
    }
    int dfs(vector<int>& jobDifficulty, int dayLeft, int idx, vector<vector<int>>& memo) {
        int n = jobDifficulty.size();
        if (dayLeft == 0 && idx == n) return 0;
        if (dayLeft == 0 || idx == n) return INT_MAX;
        if (memo[dayLeft][idx] != -1) return memo[dayLeft][idx];
        int curMax = jobDifficulty[idx], res = INT_MAX;
        for (int i = idx; i < n; ++i) {
            curMax = max(curMax, jobDifficulty[i]);
            int t = dfs(jobDifficulty, dayLeft - 1, i + 1, memo);
            if (t != INT_MAX) {
                res = min(res, t + curMax);
            }
        }
        return memo[dayLeft][idx] = res;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/1335

參考資料：

https://leetcode.com/problems/minimum-difficulty-of-a-job-schedule

https://leetcode.com/problems/minimum-difficulty-of-a-job-schedule/solutions/490316/java-c-python3-dp-o-nd-solution/

https://leetcode.com/problems/minimum-difficulty-of-a-job-schedule/solutions/944828/short-dp-solution-with-highly-detailed-step-by-step-explanation/

LeetCode All in One 題目講解匯總(持續更新中...)