讀吳恩達算-EM算法筆記
最近感覺對EM算法有一點遺忘,在表述的時候,還是有一點說不清,于是重新去看了這篇<CS229 Lecture notes>筆記. 于是有了這篇小札.
關于Jensen's inequality不等式:

Corollary(推論):
如果函數f(x)為凸函數,那么在 f(x) 上任意兩點X1,X2所作割線一定在這兩點間的函數圖象的上方,即:

舉例子: 當t=1/2 ; 1/2*f(x1) + 1/2*f(x2) >= f( 1/2*x1 + 1/2*x2 );
或者我們直接抽象的表示為: E[f(X)] ≥ f(EX) ,其中E表示期望.
那么這個 Jensen's inequality(Jensen's 不等式在EM算法中起到什么作用呢?)這里我們先不表.
關于極大似然評估(MLE):
假定存在一個樣本集 D= {x1,x2,...,Xm },為M個獨立分布的樣本. 假設似然函數為: 聯合概率密度函數P(D ; θ) ,其中(P(D ; θ)這種表示相當于P(D),只是存在未知參數θ)
我們知道了似然函數之后,將樣本數據展開:
P(D ; θ) = p(x1,x2,...,Xm;θ) = ∏mi=1 p(xi ; θ)
我們令 L( Z ) = ∏mi=1 p(xi ; θ) ,如果存在θi 使得 L(θ)最大,我們認為θi為θ的極大似然估計量,同時我們認為θi(x1,x2,...,xm)為樣本集D的極大似然函數估計量
關于求解極大似然函數:
求使得出現該組樣本的概率最大的θ值。
θi = argmax(L(θ)) = argmax( ∏mi=1 p(xi ; θ) );
繼續回到上面的公式:
L( θ ) = ∏mi=1 p(xi ; θ); 要使得L(θ)最大,那么對這個公式進一步化解:
等價于: log( L(θ) ) = log( ∏mi=1 p(xi ; θ) ) = ∑m i=1 P(xi ;θ)
(∑m i=1 P(xi ;θ))' = d( ∑m i=1 P(xi ;θ) ) / d(θ) =0 ; 求導 得 θ的解
關于極大似然求解的步驟:
(1)寫出似然函數;
(2)對似然函數取對數,并整理;
(3)求導數;
(4)解似然方程。
我們先來看文章給出的這樣一個問題:
比如我們有一個訓練集合X={ x1 , x2 , .... , Xm};里面包含M個樣本. 我們希望將模型p(x,z)的參數與訓練集合數據進行擬合,其中的函數-對數似然是:

我們想上面求解極大似然函數一樣來求解這個似然函數:
對它進行微分方程,求導 d( L(θ) ) / d( θ ) =0; ? 我們很快就發現無法求解,因為存在新的未知變量Z(隱變量);如何來解釋這個隱變量Z呢?
比如這樣一個例子:
比如有A,B兩個人比賽隨機打靶,每個人每次打4槍,當命中九環以內,包括九環,是記錄為1,否則記錄為0; 但是由于裁判熬夜玩游戲,比賽完成是,收集比賽結果時,搞混了靶紙。于是整理出如下結果:
| 人名 | 結果 |
| 未知 | 1011 |
| 未知 | 0011 |
| 未知 | 1101 |
| 未知 | 0101 |
| 未知 | 1011 |
| 未知 | 0010 |
| 未知 | 1111 |
| 未知 | 1011 |
問A命中九環的概率pa,B命中九環的概率pb?
而這里的隱變量Z就是人名的順序。
面對這個問題,顯然使用極大似然函數去正面扛困難重重,EM算法為這個問題,提供了一個很好的思路:
求解分兩步走:
E step 期望階段:
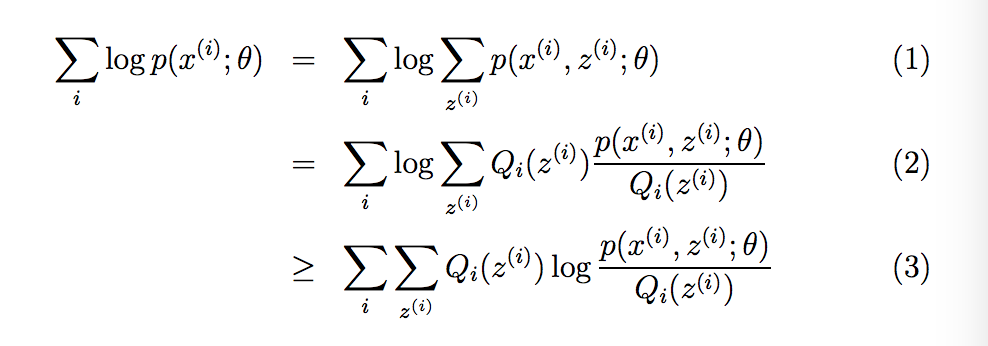
先假定,即初始化A,B命中的概率pa0=0.2 , pb0=0.5;
求出8次打靶中,該次打靶的結果是A,B的可能性即概率:
第一次打靶:如果是A的打靶結果: 0.2*0.8*0.2*0.2=0.0064
如果是B的打靶結果: 0.5^4 =0.0625
| 第i次打靶 | A | B |
| 1 | 0.0064 | 0.0625 |
| 2 | 0.0256 | 0.0625 |
| 3 | 0.0064 | 0.0625 |
| 4 | 0.0256 | 0.0625 |
| 5 | 0.0064 | 0.0625 |
| 6 | 0.1024 | 0.0625 |
| 7 | 0.0016 | 0.0625 |
| 8 | 0.0064 | 0.0625 |
如此,我們依據極大似然函數,來確定每一輪是誰打的
1輪: P(A1)<P(B1),
由上面這個表,我們在假定的前提下,計算出了A或者B的出現每輪打靶結果的概率;我們可以依據這個結果,進一步計算第i次是A,B打靶的相對概率
求出8次打靶中,該次打靶的結果是A,B的相對可能性即概率:
第一次打靶:如果是A的打靶結果: 0.0064/(0.0064 + 0.0625) =0.0928
如果是B的打靶結果: 0.0625/(0.0064 + 0.0625) =0.9072
| 第i次打靶 | A | B |
| 1 | 0.0928 | 0.9072 |
| 2 | 0.290 | 0.710 |
| 3 | 0.0928 | 0.9072 |
| 4 | 0.290 | 0.710 |
| 5 | 0.0928 | 0.9072 |
| 6 | 0.620 | 0.380 |
| 7 | 0.0249 | 0.9751 |
| 8 | 0.0928 | 0.9072 |
我們先假定A,B命中的概率pa1,pb1,然后去推到它們比賽的順序,再依據比賽的順序,來計算A,B命中的概率Pa2,pb2. 當pa2,pb2和pa1,pb2結果相差時較大時,
將pa2,pb2代入,繼續推到它們的比賽順序,計算A,B命中的概率



 浙公網安備 33010602011771號
浙公網安備 33010602011771號