離散數學(圖與網絡)
圖
圖的基本概念
簡單圖:不允許有平行邊和反身邊。
無向圖:允許有平行邊和反身邊。
有限圖:有限點構成的圖一定是有限圖,但是有限邊構成的圖不一定是有限圖(可能有無數個孤立點)
零圖:只有點,沒有邊。
完全圖:任意兩點之間都有邊。邊的數量是\(\mathrm{C}_{\mathrm{m}}^{2}\) (m是頂點數)

圖的同構:圖經過一系列物理變化(伸縮、旋轉),變化前后的兩個圖看成同一個圖

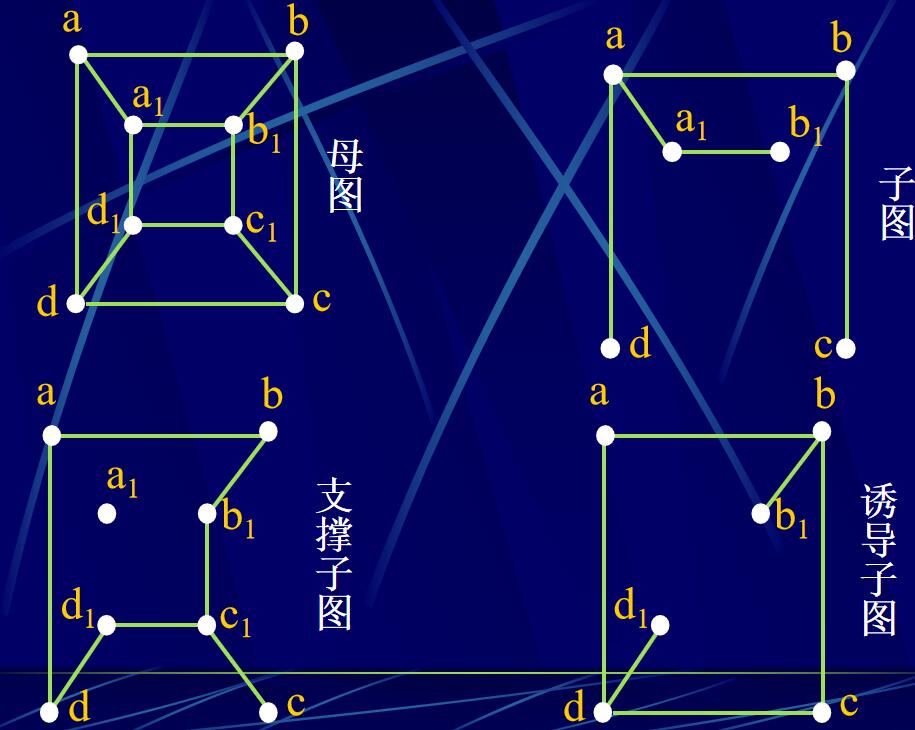
母圖
子圖:母圖的一部分
支撐子圖:點與母圖一致,邊可以少
誘導子圖:去點母圖某個(些)點的同時把與點相連的邊去掉。
度:\(d_G\left( v \right)\)與某點相連的邊的個數。 度為0的點為“孤立點”
關聯矩陣:表示點和邊之間的關系
特點:
-
每一列之和一定為2,因為每一條邊一定只有兩個頂點
-
每一行之和表示該頂點的度,因為表示它是某一個邊的頂點
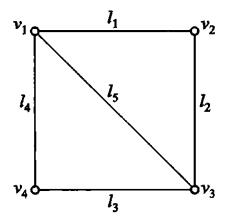
鄰接矩陣:表示點與點之間有沒有邊
特點:
- 主對角線元素為0
- 對稱矩陣
- 每一行或每一列之和表示頂點的度
定理4.1.1:所有點的度數之和是邊數的二倍(所有點的度數之和一定是偶數)
定理4.1.2:在任一有限圖中,奇數點的個數為偶數
證明:由定理4.1.1,且知道偶數點的度之和一定是偶數,那么奇數點的度數之和一定也是偶數,那么奇數點的個數也一定是偶數
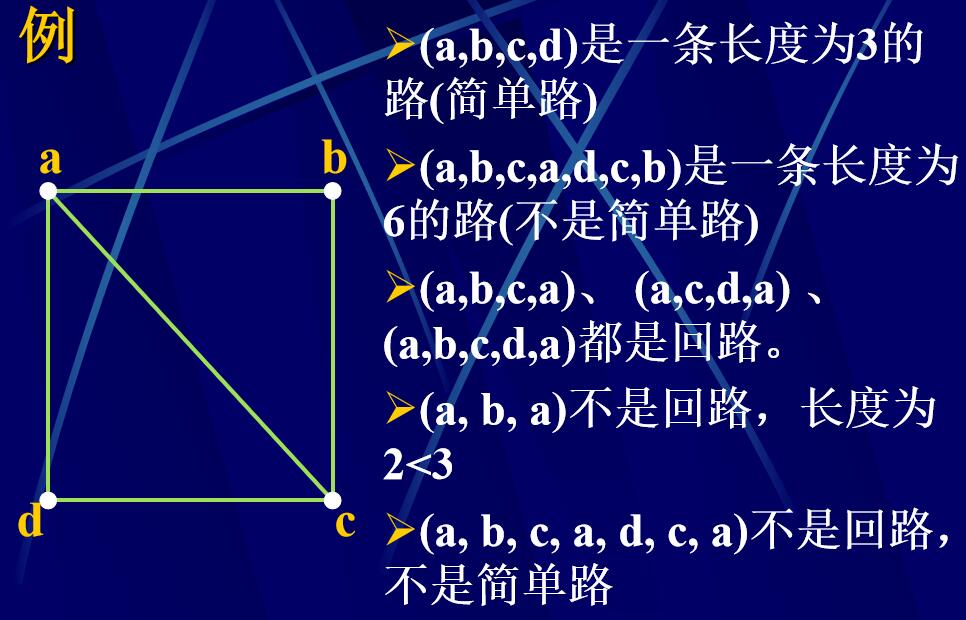
簡單路:除開頭v0和結尾點vn可以相同以外,路徑上的點不可以相同
回路:G中從點v到自身的長度不小于3的簡單路
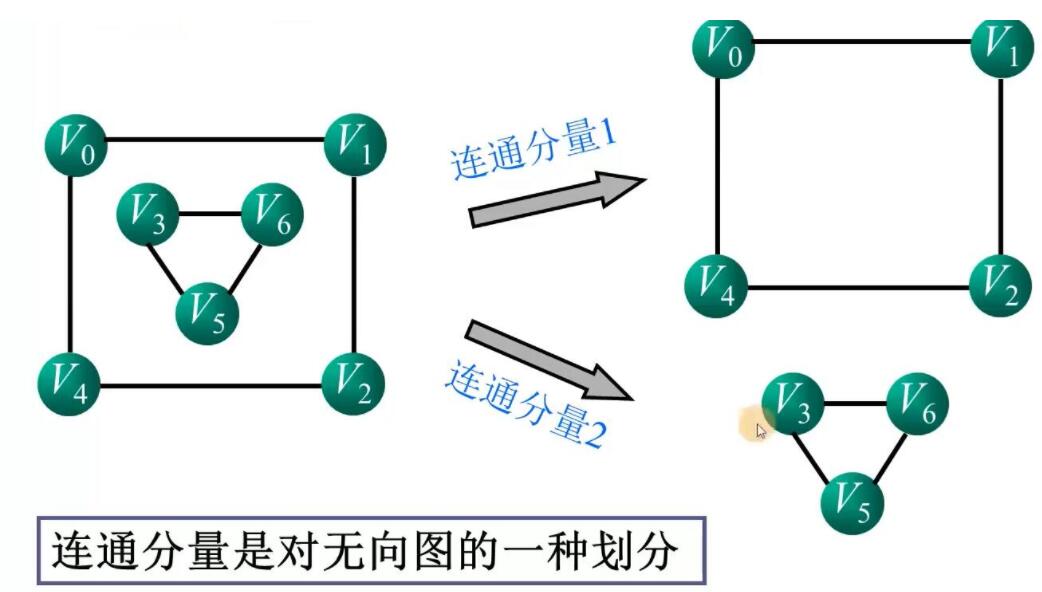
相連:從u到v有一條路(v與自身相連)
連通分支:非連通圖的極大連通子圖
證明一個圖是連通圖的方法:
1.直接證明
2.反證法
常考定理:設G=(P,L)是有限圖,P(G),L(G)的元數分別為m,n。證明:如果n> \(\mathrm{C}_{\mathrm{m}-1}^{2}\) ,則G是連通的。(至少m-1個點之間都有邊)
證明:反證法。假設此時G不是連通的,則將G中的一個連通分支作為一個子圖記為G1,剩余的部分記為G2。可設P(G1)的元數為m1,P(G2) 的元數為m2,其中1≤m1,m2<m,m1+m2=m。則:
n≤m1(m1-1)/2+ m2(m2-1)/2=1/2(\(\mathrm{m1}^2\)+\(
\mathrm{m2}^2
\)- m1- m2)
=1/2( \(
\mathrm{(m1+m2)}^2\)- 2m1m2 - ( m1+ m2 ))
=1/2(\(\mathrm{m}^2\)-m-2m1m2)
由于(m1-1) (m2-1) ≥0所以有:
m1 m2- (m1+m2)+1≥0 即 m1 m2≥ m-1,則有:
n≤1/2(\(\mathrm{m}^2\)-m-2m1m2)≤1/2(m2-m-2(m-1))
=1/2(m2-3m+2)=1/2(m-1)(m-2)= \(\mathrm{C}_{\mathrm{m}-1}^{2}\)
例題:有限圖G,|P(G)|=6,|L(G)|=11,則G可能不是連通圖(X)
解:\( \mathrm{L}\left( \mathrm{G} \right) =11>\mathrm{C}_{5}^{2}=10\) 一定連通
權圖 Dijkstra算法(單源點最短路徑問題)
權值:帶有某種含義的邊
最短路徑:兩頂點之間經歷的權值之和最短的路徑
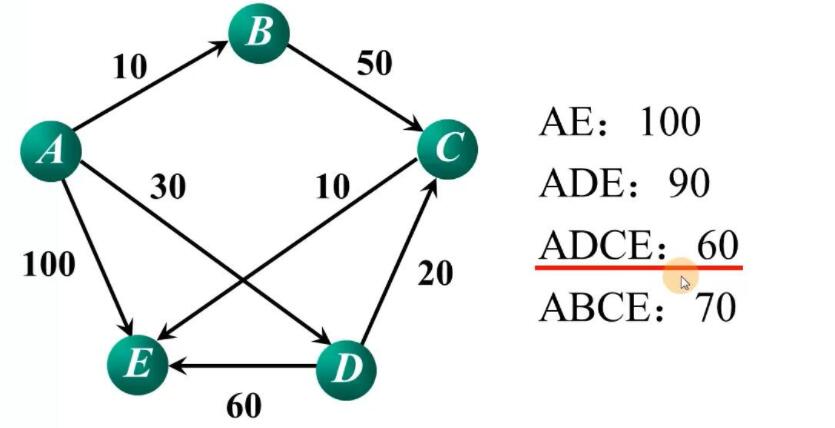
Dijkstra算法
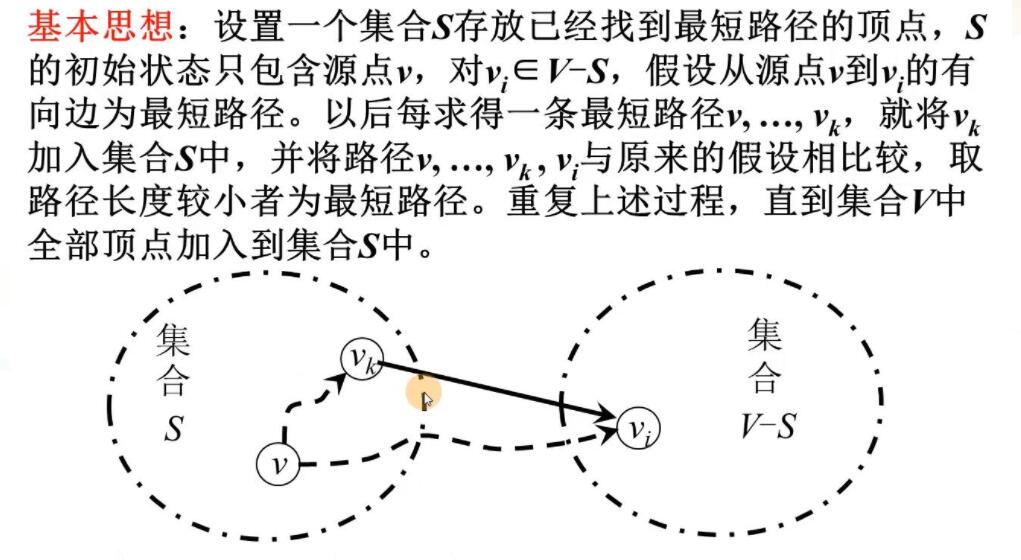
Dijkstra算法演示
例一
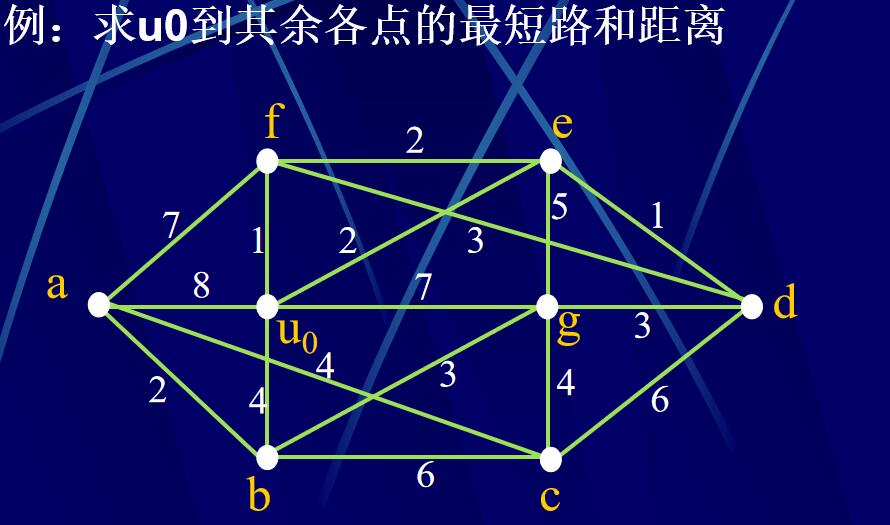
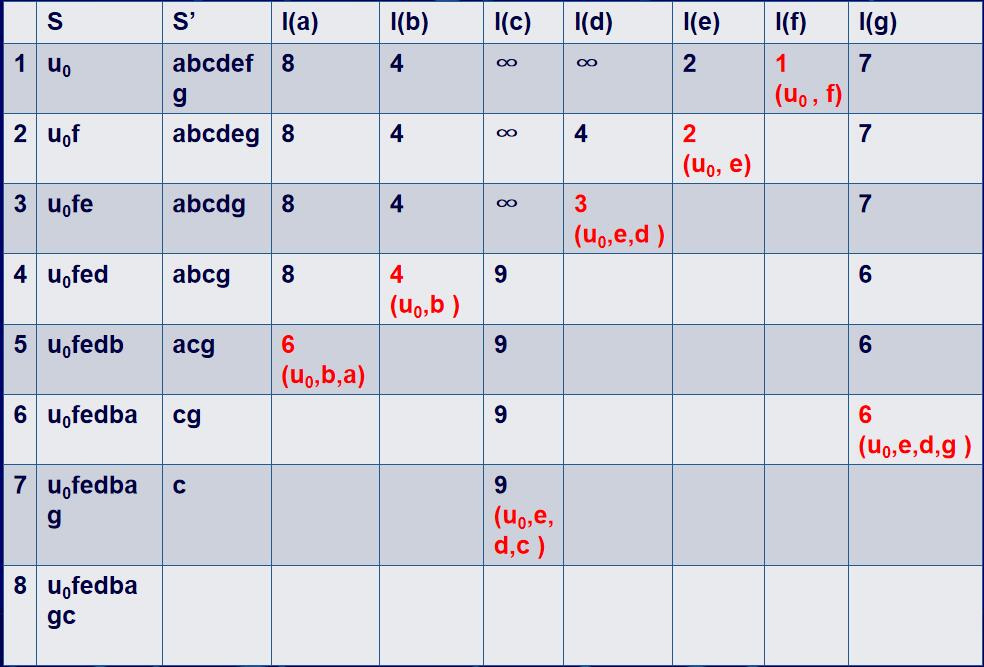

例二

首先確定是一個鄰接矩陣,可以畫出權圖,求A到其他點的最短路徑
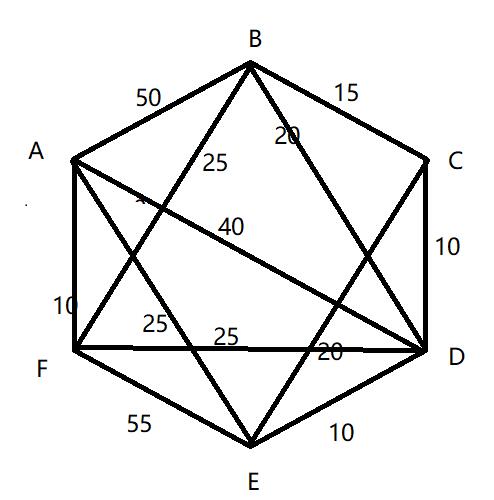
列表:
| S | S' | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | BCDEF | 50 | \(\infty\) | 40 | 25 | 10(AF) |
| AF | BCDE | 35(AFB) | \(\infty\) | 35(AFD) | 25(AE) | |
| AFE | BCD | 35(AFB) | 45(AEC) | 35(AFD)(AED) | ||
| AFEB | CD | 45(AEC) | 35(AFD)(AED) | |||
| AFEBD | C | 45(AEC)(AFDC)(AEDC) | ||||
| AFEBDC |
第一輪:
l(B)=w(AB)=50,l(C)=w(AC)= \(\infty\) ,l(D)=w(AD)=40,l(E)=w(AE)=25,l(F)=w(AF)=10
第二輪:
l(B)=min{l(B),l(F)+w(FB)}=min{50,10+25}=35
l(C)=min{l(C),l(F)+w(FC)}=min{ \(\infty\) , \(\infty\) }= \(\infty\)
l(D)=min{l(D),l(F)+w(FD)}=min{40,10+25}=35
l(E)=min{l(E),l(F)+w(FE)}=min{25,10+55}=25
第三輪:
l(B)=min{l(B),l(E)+w(EB)}=min{35,25+ \(\infty\) }=35
l(C)=min{l(C),l(E)+w(EC)}=min{ \(\infty\) ,25+20}=45
l(D)=min{l(D),l(E)=w(ED)}=min{35,25+10}=35
第四輪:
l(C)=min{l(C),l(B)+w(BC)}=min{45,35+15}=45
l(D)=min{l(D),l(B)+w(BD)}=min{35,35+20}=35
第五輪:
l(C)=min{l(C),l(D)+w(DC)}=min{45,35+10}=45
?
A==>B:35(AFB)
A==>C:45(AEC)(AFDC)(AEDC)
A==>D:35(AFD)(AED)
A==>E:25(AE)
A==>F:10(AF)
樹
樹及其等價定義
定義4.2.1:設G=(P,L)是圖,如果G是連通的,并且無回路,則稱G為樹.無回路的圖(可能不連通)也稱為森林.
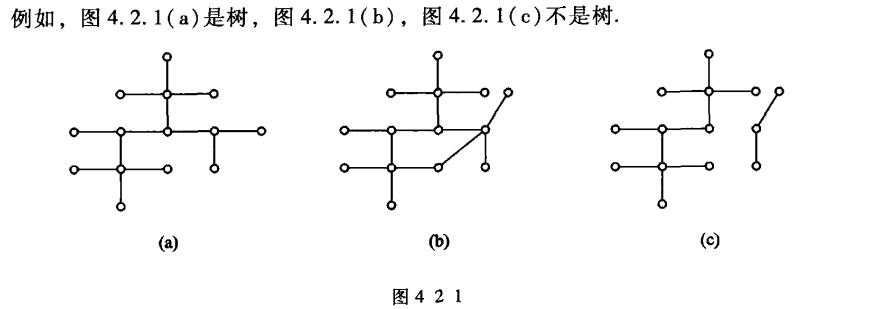
引理4.2.1:設G是至少有一條邊的有限圖,且無回路,則G至少有一個點只相鄰于另一個點,即G至少有一個點度數為1.
定理4.2.1:如果G是圖,則下列諸命題等價.
(1)G是樹.
(2)G連通并且刪去G的任意一邊,所得到的圖都不連通.
(3)對G中任意兩點v,v'(v≠v'),恰有一條從v到v'的簡單路.
如果G還是有限圖,設P(G)元數為n,則下列命題也與上面的命題等價.
(4)C不含回路,并且G有n -1條邊.
(5)G連通,并且G有n -1條邊.
推論4.2.1:任意有限連通圖必有一支撐子圖是樹。今后,此支撐子圖稱為母圖的支撐樹.
推論4.2.2:若G'是有限圖G的支撐樹,w'為G中一邊,且 w'不在G'中,則G'添上邊'后必有回路.
Kruskal算法
定義4.2.2:設G是加權連通圖,帶有最小權(和)的支撐樹稱為權圖G的最優樹。
設權圖G=(P, L)是連通的。
在L(G)中選一個具有最小權值的邊,記為\(l_1\),令T={ \(l_1\) };
從L(G)-T中取\(l_i\),使得T∪{\(l_i\)}不產生回路,并且w(\(l_i\))最小。如果存在這樣的\(l_i\),則令T= T∪ {\(l_i\)},重復步驟2);
如果不存在這樣的\(l_i\),則算法停止。
白話:每次選取權值最小的邊,前提是不能產生回路,如果產生回路需要換一條次小的回路,......直到選出n-1條邊(n是點的個數)。
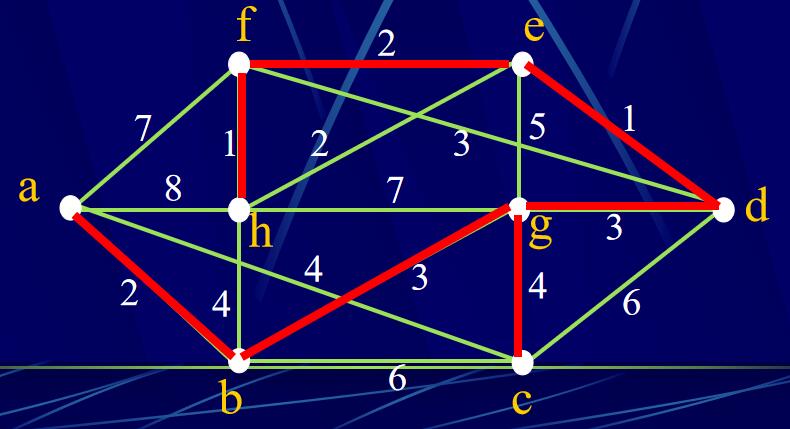
樹的常用結論:
1.每一株恰好有兩個點度是1的樹必是一條簡單路(d=2(n-1))
2.若G為?≥k的樹,其中?是G中點的最大度,則G最少有k個點的度是1(d=2(n-1))
有向圖 Euler路
有向圖
定義4.3.1 :G=(P, A)稱為有向圖,如果P是點集合,A是從一點引到一點(不要求一定是另一點)的弧集合。當P為有限集時,G稱為有限有向圖.若e是一條從點v到點v’的弧,則稱v為e的起點,記為v=init(e);v’為e的終點,記為v’=fin(e).
起點和終點都是點v的弧稱為反身弧。

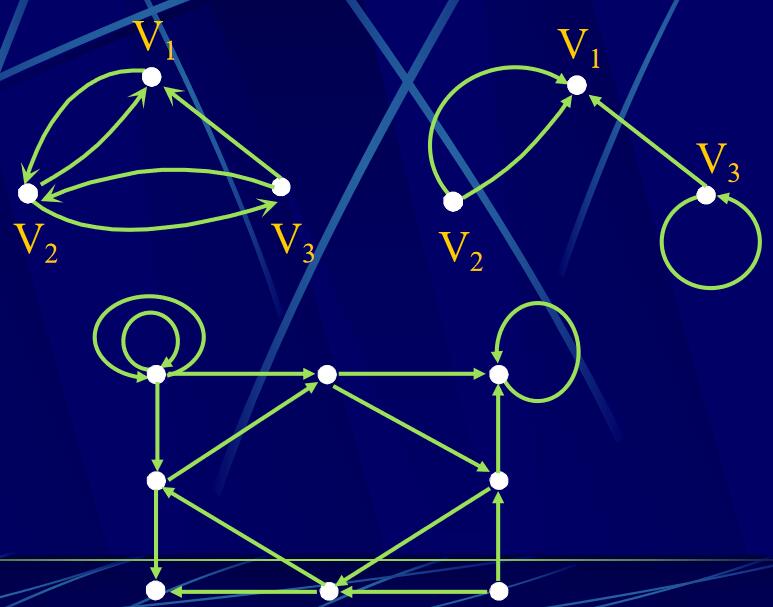
出度(輸出次數)、入度(輸入次數)、度(輸入加輸出)
有向子圖(P(H) \(\subseteq\)P(G),A(H)\(\subseteq\)A(G))、支撐子圖(P(H)=P(G))
有向路
簡單有向路(簡單路):有向圖的有向路,n條弧的起點互不相同,n條弧的終點也互不相同
有向回路:從點v到自身的簡單有向路(長度可以為1或2)稱為有向回路,是簡單路。

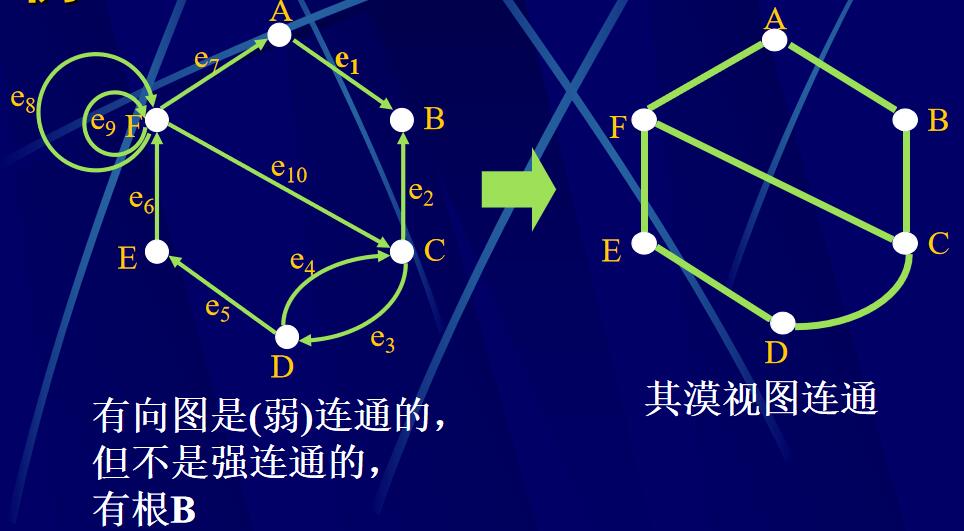
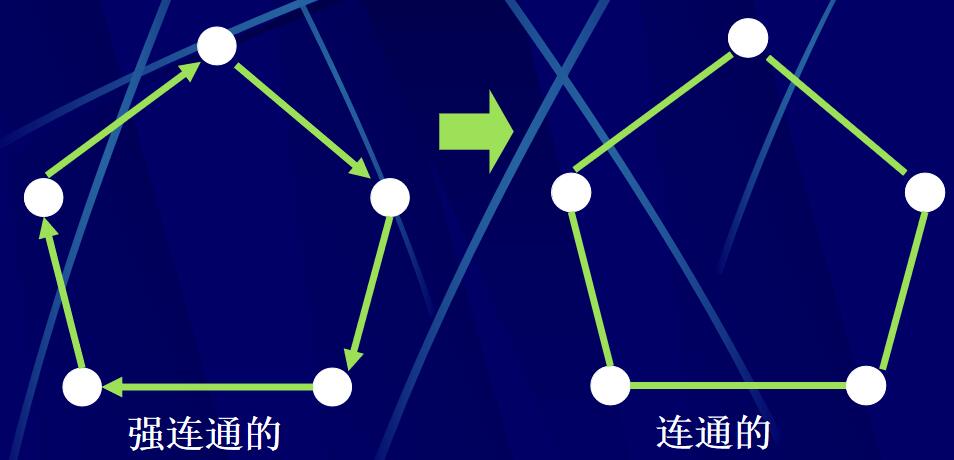
強連通:設G=(P,A)是有向圖,對G中任意兩點v,v’ (v\(\ne\)v’),如果都有從v到v’的有向路,則稱G是強連通的。有從任意點到任意點的路)
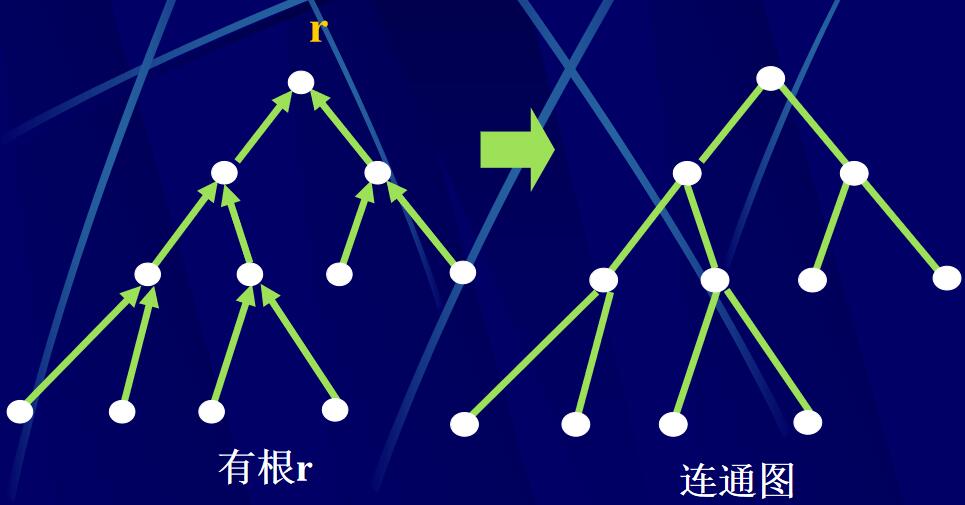
根:設G=(P,A)是有向圖,r\(\in\)P(G)。稱r為G的根,如果對G中任一點v (v\(\ne\)r),都有從v到r的有向路。(所有點有到根的路)

漠視圖:
(1)刪去G中自身到自身的弧(反身弧);
(2)G中任意兩點,若有弧,只保留一條;
(3)刪去弧的方向,即得\(\mathrm{G}_0\)。

弱連通:漠視圖連通。
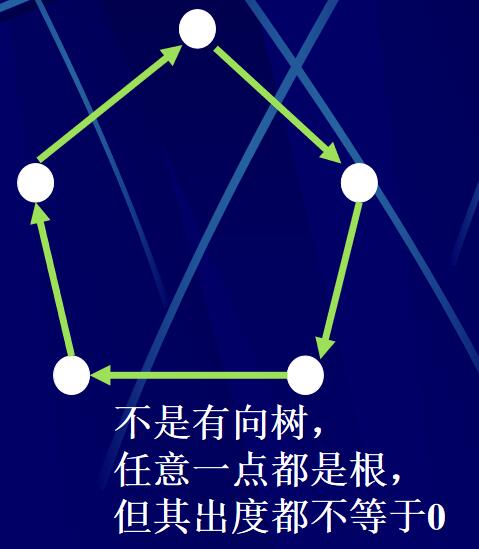
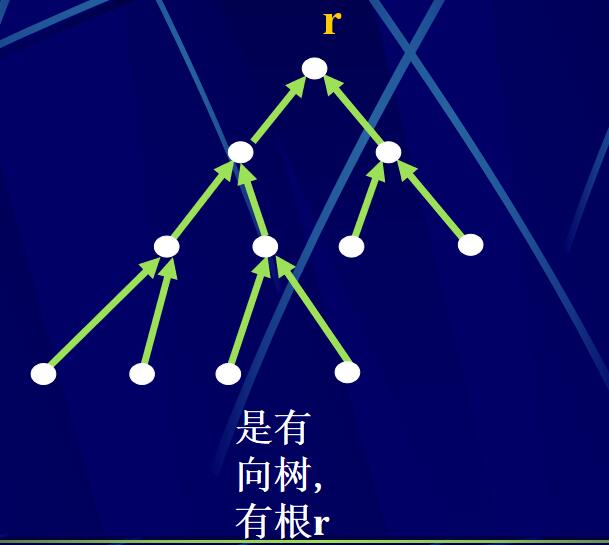
有向樹:
有向圖G稱為有向樹(或有根樹),如果G中有一點r,并且滿足:
(1) G中每一點v(v\(\ne\)r)都恰是一條弧e的起點;
(2) r不是任一條弧的起點;
(3) r是根。
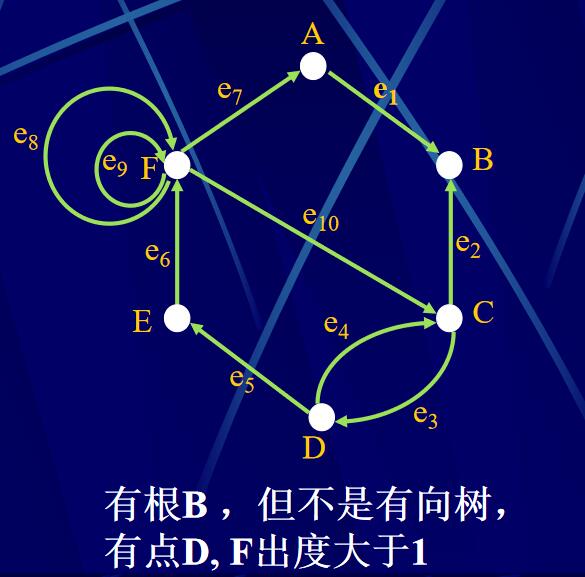
有向樹的特點:
- 每一點v(v\(\ne\)r)到r恰有一條有向路;
- 沒有有向回路;
- 兩點間最多有一條弧。
轉化定理:
對有向樹G,若無視各弧之方向,則得一樹\(\mathrm{G}_0\); (--命題1)
反之,若\(\mathrm{G}_0\)是樹,可選取任一點做根,并適當指定各邊之方向,則得一有向樹G。(--命題2)
Euler路
Euler路:(注意這個圖很重要)
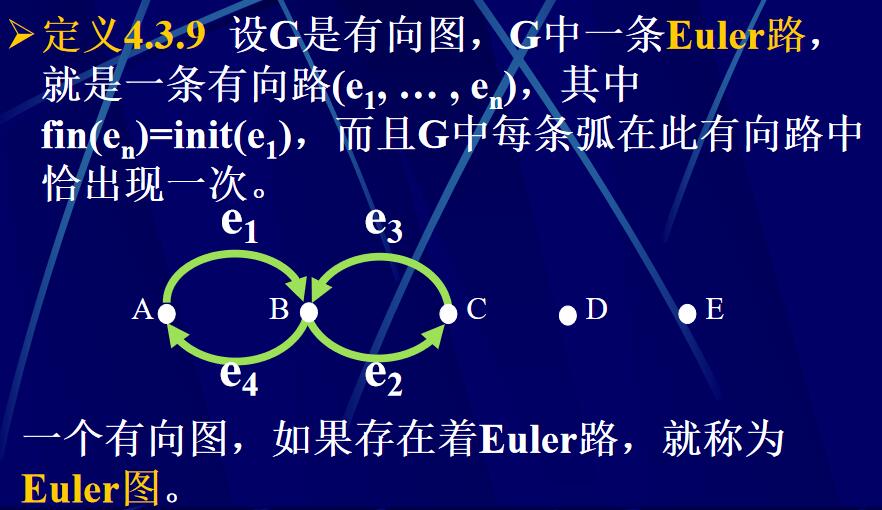
Euler路實際上是一條封閉的一筆畫路線

平衡有向圖:設G是有向圖。如果G中每點v,都有有限的輸入次數和輸出次數,而且輸入次數和輸出次數相等。
一有限平衡有向圖,其弧數必有限。
一有向圖若存在Euler路,則必平衡。
判定Euler圖的充要條件:設G是無孤立點的有限有向圖。于是,G有Euler路當且僅當G是平衡的,并且強連通。
推論:設G是無孤立點的有限有向圖,于是,G有Euler路當且僅當G平衡,并且將G漠視為圖\(\mathrm{G}_0\)時是連通的(弱連通) 。
哈密頓(Hamilton)圖
Hamilton路 Hamilton圖的必要條件
定義4.4.1 設G=(P, L)是有限圖,(v1, … , vn)是G中一條路。如果G中每點恰在此路中出現一次,則稱此路為Hamilton路。
如果G中每點,除v1外,恰在此路中出現一次,而v1=vn,則此路稱為Hamilton回路。
定義4.4.2 設G=(P, L)是有限圖,如果G中有一條Hamilton回路,則稱G為Hamilton圖。
比較Hamilton路、Hamilton回路與Euler路:
Hamilton路一定為簡單路;
Euler路未必簡單有向路。
Hamilton路著眼于無重復地遍歷圖中諸點;
Euler路著眼于無重復地遍歷有向圖中諸弧。
Hamilton路、Hamilton回路是G的支撐子圖,
Hamilton路是G的支撐樹;
Euler路未必為G的支撐子圖。
存在Euler路,未必存在 Hamilton回路。
存在Hamilton回路,未必存在Euler路。
Hamilton路和Hamilton回路的性質
- 若圖中有一點的度為1,則無Hamilton回路。
- 若圖中有一點的度為0,則既無Hamilton路,
又無Hamilton回路。 - 設圖中有一點的度為2,若有Hamilton回路,
則以此點為端點的兩條邊均出現在此回路中。 - 設圖中有一點的度大于2,若有Hamilton回
路,則只用其中的兩條邊。 - 若圖中有n個點,則
Hamilton路恰有n-1條邊,
Hamilton 回路恰有n條邊。 - Hamilton路是圖G的支撐子樹,
Hamilton回路是圖G的支撐子圖。
Hamilton路、Hamilton圖的必要條件
定理4.4.1: 如果圖G=(P, L)是Hamilton圖,則對P(G)的任一非空子集S,都有W(G-S) \(\leqslant\) |S|(連通分支數小于等于去掉的點的個數)
其中:
|S| 表示集合S的元素數,S就是刪除的點集
G-S表示在G中刪除S中的點以及以S中的點為端點的所有邊而剩下的圖(誘導子圖),
W(G-S)表示圖G-S的連通分支數。
常用其逆否命題用來證明該圖不是Hamilton圖(如果連通分支數大于去掉的點的個數則不是Hamilton圖)
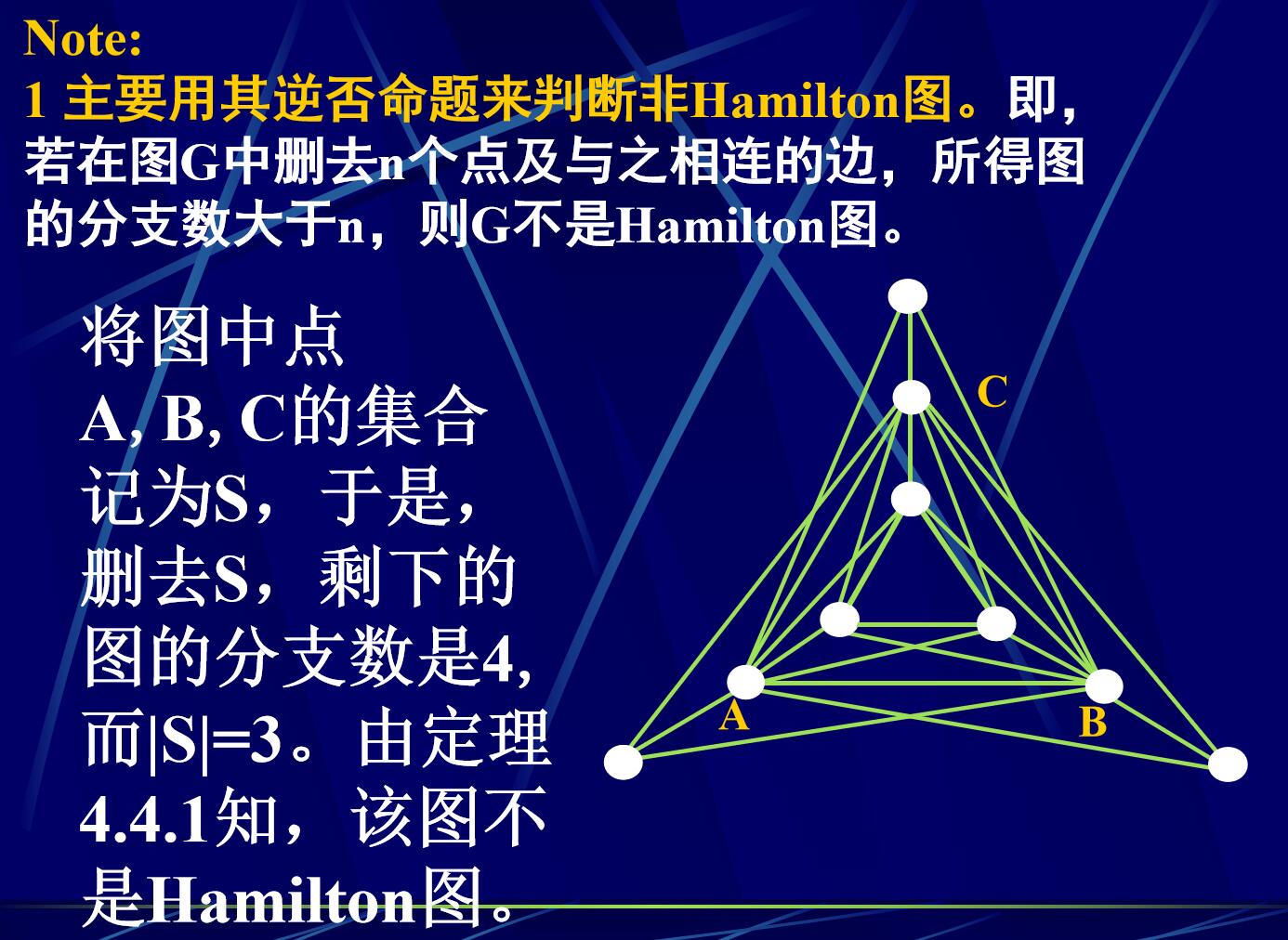

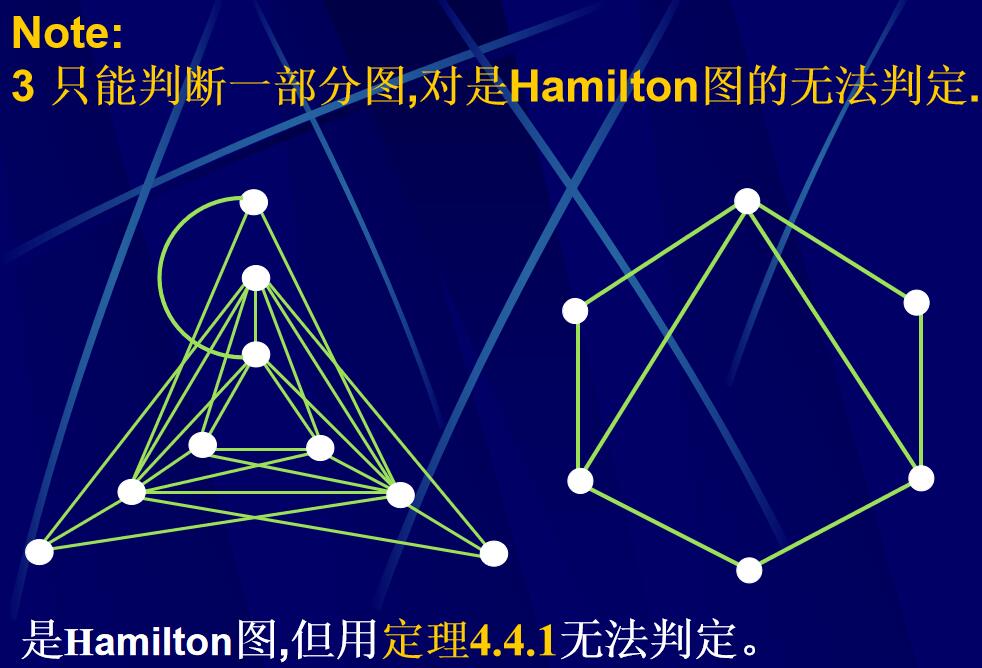
Hamilton圖的充分條件
定理4.4.2:若G=(P, L)是有限圖\(\gamma \geqslant 3\text{,}\delta \geqslant \gamma /2\),則G是Hamilton圖。
其中,\(\gamma\)表示圖G中點數,即\(\gamma\)=|P(G)|,
\(\delta\)表示G中點的最小度。
白話:點數大于等于3,點的最小度大于等于點總數的二分之一
引理4.4.1:設G是有限圖,u, v是G中不相鄰的兩點,并且滿足:d(u)+d(v) $\geqslant \gamma $,則G是Hamilton圖的充要條件是G∪{uv}是Hamilton圖。
閉合圖:設G是有限圖。反復連接G中不相鄰的并且其度之和不小于\(\gamma\)的點對,直到沒有這樣的點對為止。最后所得的圖稱為G的閉合圖,記為C(G)。
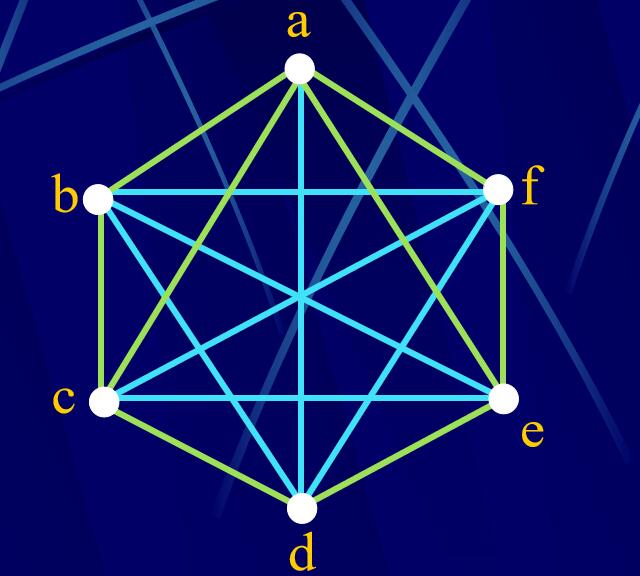
引理4.4.2 :有限圖G的閉合圖C(G)是唯一確定的
定理4.4.3:有限圖G是Hamilton圖的充要條件是閉合圖C(G)是Hamilton圖。
推論:設G是有限圖,若C(G)是完全圖,則G是Hamilton圖
推論的逆不成立:若G是Hamilton圖,則C(G)未必是完全圖
(定理4.4.3強于4.4.2)
常用結論:若一個圖G的任意兩點度數之和≥n-1,n=|P(G)|≥3,則該圖有Hamilton路。
證明:
向圖G中增加一個點v,并且連接v點與G中已有的n個點,設得到的圖為G’, 這樣:G’中點v的度為n,G中的n個點在G’中的度分別增加了1;從而有:G’中來自G的任意兩個點的度數之和≥n-1+1+1=n+1;
而G’中v點與其他任意點的度數之和≥n+1;這樣,G’中任意兩點度數之和≥n+1=|P(G’)|。
則G’的閉合圖是完全圖,根據定理4.4.3的推論,可知G’是Hamilton圖,則G’中有Hamilton回路,形如:
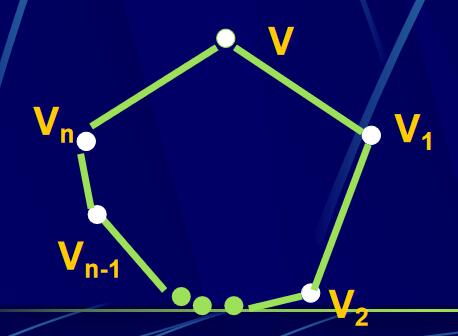
而且這條H回路只用了\(\mathrm{vv}_1\), \(\mathrm{vv}_n\)這兩條新增加到G中的邊,從而刪除v點,G中存在Hamilton路.
定理4.4.4 :設有限圖G的度序列(即G的各點的度,按非降序排成的序列)為(d1,d2,…,\(d_{\gamma}\)),其中d1\(\leqslant\)d2\(\leqslant\)…\(\leqslant\)\(=d_{\gamma}\),\(\gamma\) \(\leqslant\) 3.
如果不存在這樣的m, m< \(\gamma\)/2 ,并使得\(d_m\)\(\leqslant\) m , \(d_{\gamma -m}\leqslant \gamma -m\)則G是Hamilton圖。
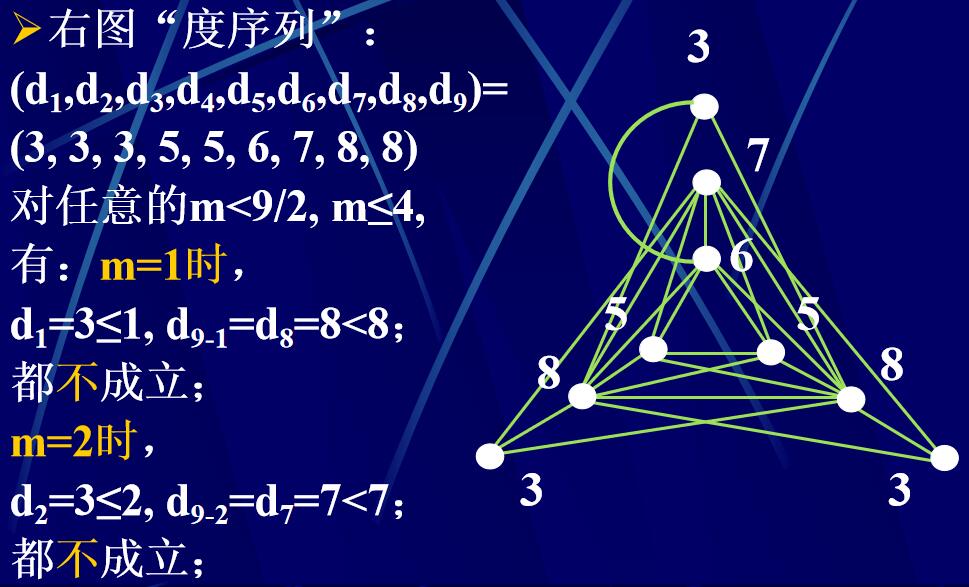
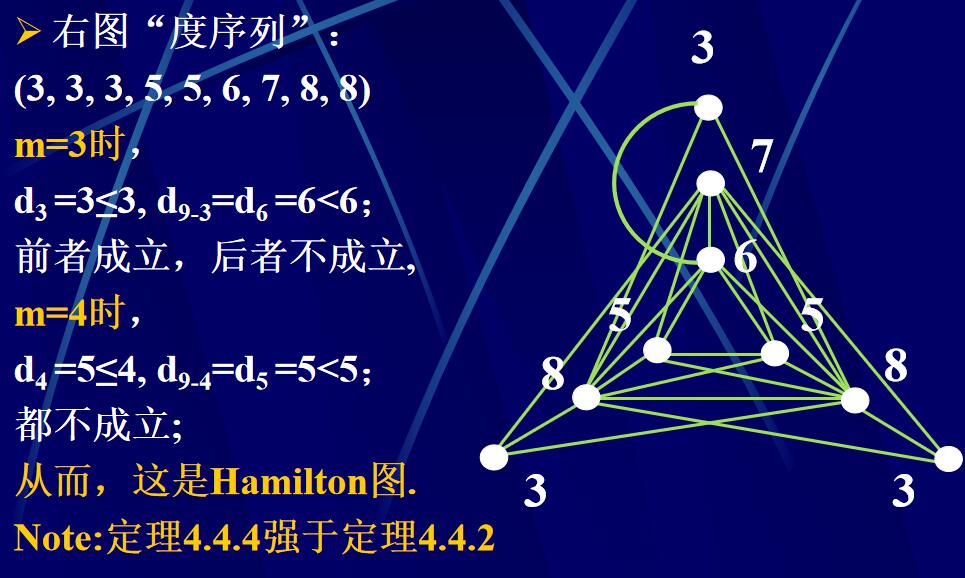
定理4.4.4強于定理4.4.2
定義4.4.4 :實數序列(p1, …, pn)稱為由實數序列(q1, …, qn)所增大,如果pi\(\leqslant\)qi, i=1,…,n 稱為不減度序列
例如: (2, 2, 2, 2)由(2, 2, 3, 3)所增大
定義4.4.5: 設G,H是有限圖。G稱為被H度增大,如果|P(G)|=|P(H)|,并且G的不減度序列被H的不減度序列所增大

定義4.4.6 :設G,H是兩個無公共點的有限圖。將G的每個點和H的每個點都用邊連接起來得到的圖,稱為G與H的連接圖
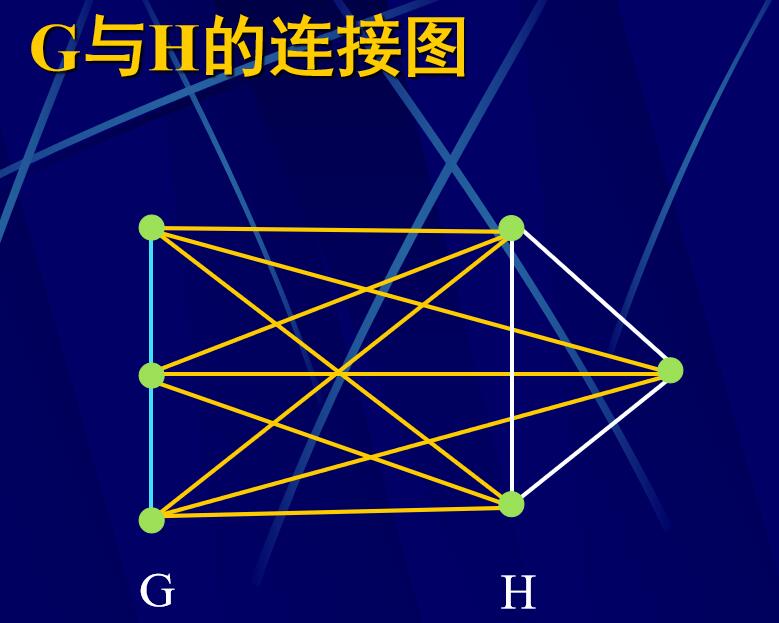
定義4.4.7: 設G,H是兩個有限圖,如果P(G)=P(H),并且對G,H中任意兩點u、v,u和v在G中相鄰當且僅當它們在H中不相鄰,則稱G是H的補圖,H是G的補圖,可以將G記為\(\mathrm{H}_{\mathrm{c}}\),也可將H記為\(\mathrm{G}_{\mathrm{c}}\)

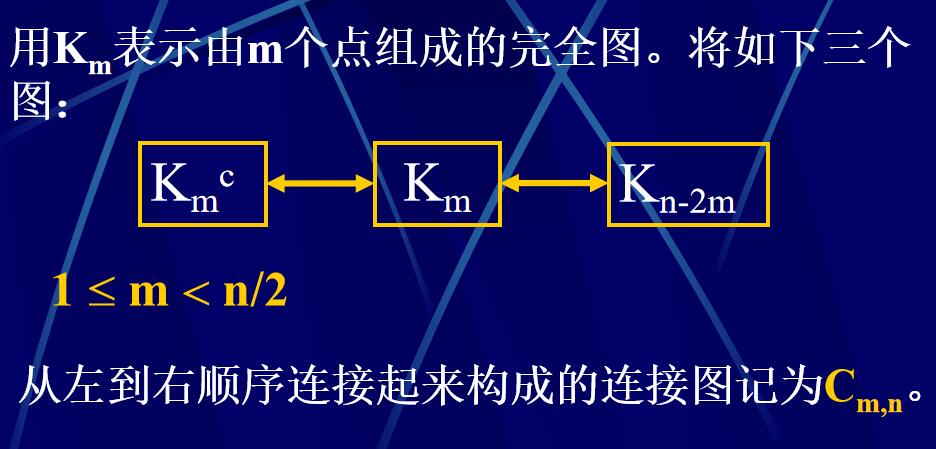
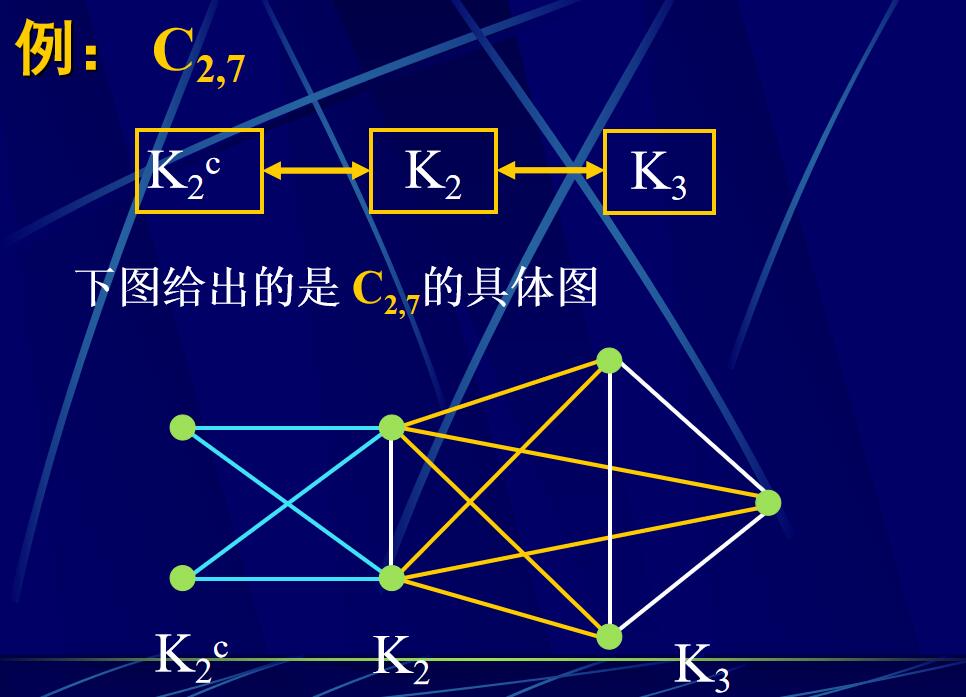
引理4.4.3:若1 \(\leqslant\) m < n/2 ,則圖 \(\mathrm{C}_{\mathrm{m},\mathrm{n}}\)是非Hamilton圖
定理4.4.5:若G為非Hamilton圖,\(\mathrm{\gamma}\geqslant\) 3,則G由某個\(\mathrm{C}_{\mathrm{m},\mathrm{n}}\)所度增大。其中\(\gamma\)是P(G)的元數。該定理的逆定理不成立
連接圖\(\mathrm{C}_{\mathrm{m},\mathrm{\gamma}}\)的不減度序列是

例如

例題:
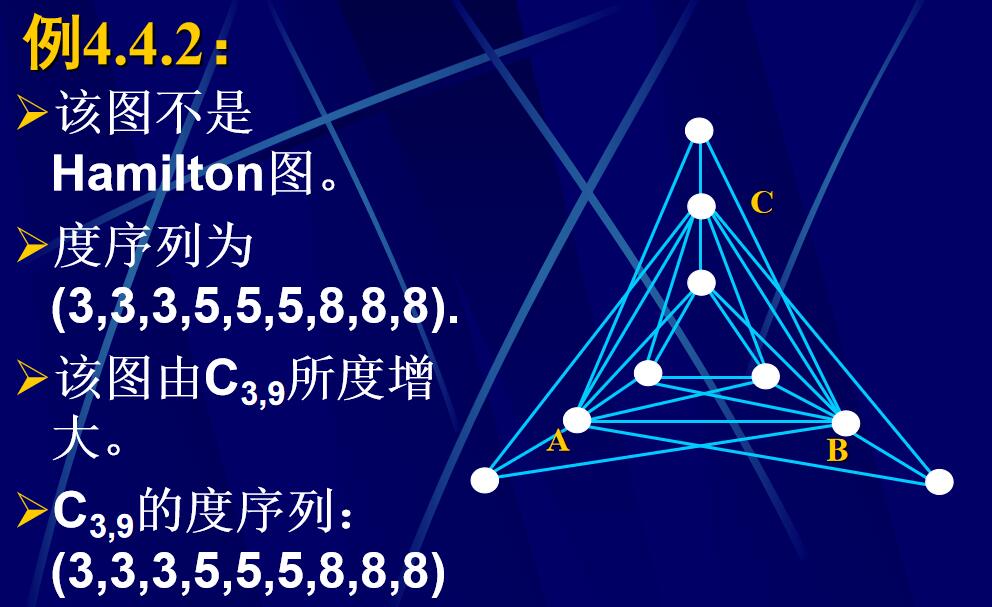
常用結論:
設G是圖,P(G)=n,L(G)=m,若 m≥\(\frac{1}{2}\)(n-1)(n-2)+2=\(\mathrm{C}_{\mathrm{n}-1}^{2}+2\),則G一定是Hamilton圖。
n個點的邊數最多的非Hamilton圖是邊數為 \(\frac{1}{2}\)(n-1)(n-2)+1=\(\mathrm{C}_{\mathrm{n}-1}^{2}+1\)的圖。(即n個點的邊數最多的非Hamilton圖是\(\mathrm{C}_{1,\mathrm{n}}\))
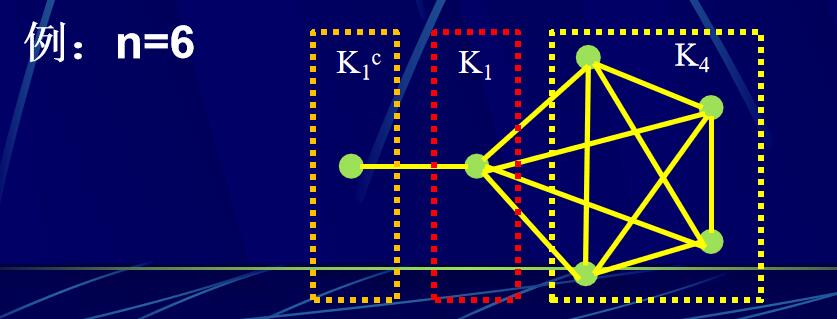
理解:之前講過當邊數m>\(\mathrm{C}_{\mathrm{n}-1}^{2}\)時也就是m\(\geqslant\)\(\mathrm{C}_{\mathrm{n}-1}^{2}\)+1時圖必定連通,此時可以理解成1個點p和\(\mathrm{K}_{\mathrm{n}-1}\)這個完全圖相連。此時沒有哈密頓回路,不是哈密頓圖,如果把這個點p和\(\mathrm{K}_{\mathrm{n}-1}\)中的任意一個點相連,由于\(\mathrm{K}_{\mathrm{n}-1}\)是哈密頓圖,p到\(\mathrm{K}_{\mathrm{n}-1}\)有路,從\(\mathrm{K}_{\mathrm{n}-1}\)到p有另一條路,這就形成了哈密頓回路,也就是形成了哈密頓圖

往期回顧
離散數學(集合論)
離散數學(古典數理邏輯)
離散數學(圖與網絡)
離散數學(數論基礎)
離散數學(格與布爾代數)
離散數學(群、環、域)


 浙公網安備 33010602011771號
浙公網安備 33010602011771號