loading...

[hdu6566]The Hanged Man

A. The Hanged Man on hdu

給 \(n\) 個(gè)節(jié)點(diǎn)的一棵樹(shù) \((V,E)\)，每個(gè)節(jié)點(diǎn)有權(quán)值 \(a_i,b_i\)，定義：

\(f(x)\) 為：在樹(shù)上選一些節(jié)點(diǎn)得到節(jié)點(diǎn)集合 \(S\) 滿足 \(\forall (u,v) \in E:u\notin S \lor v\notin S\)，\(f(x)\) 為這些集合中滿足 \(\sum _{i\in S} a_i=x\) 且 \(\sum _{i\in S}b_i\) 最大化的個(gè)數(shù)。求 \(1 \sim m\) 的 \(f(x)\)。

\(1\le n\le50, 1 \le a_i\le m \le 5000, b_i \le 10^6\)

易得暴力 dp。\(f_{i,j,0/1}\) 為節(jié)點(diǎn) \(i\) 選/不選時(shí)，和為 \(j\) 的方案數(shù)，注意要維護(hù)一個(gè)輔助的數(shù)組表示最大值。

這里樹(shù)上背包合并 \(\mathcal O(m^2)\) 無(wú)法承受，考慮轉(zhuǎn)為熟悉的序列背包合并（單次 \(\mathcal O(m)\)，總共 \(n\) 次）。

將節(jié)點(diǎn)按樹(shù)上 \(\tt dfs\) 序重標(biāo)號(hào)后轉(zhuǎn)移。考慮 \(i \to i+1\) 時(shí)的情況。

\(\mathrm{fa}_{i+1}=i\)，這種情況最好，只需使用 \(i\) 的信息轉(zhuǎn)移即可。
\(\mathrm{fa}_{i+1}\neq i\)，\(i+1\) 跳到另一棵子樹(shù)去了。這時(shí)就要求我們之前轉(zhuǎn)移時(shí)得存下它的父親。哪些是需要存的呢？

一張圖

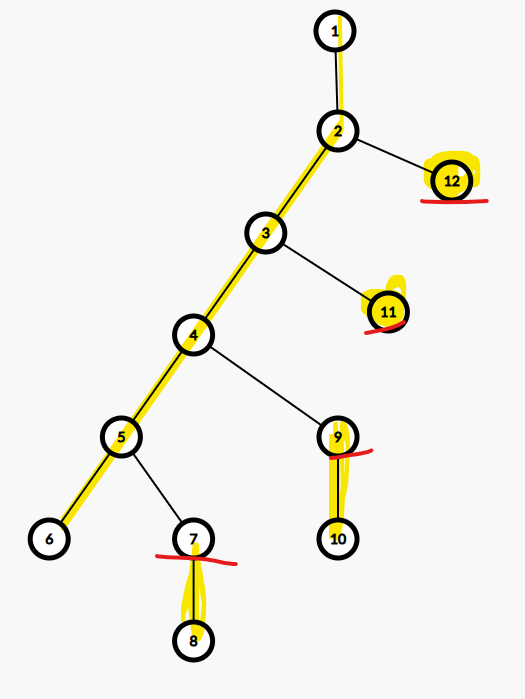
如圖，用紅色標(biāo)記出來(lái)的是跳躍的點(diǎn)，他們的父親都是需要提前存下來(lái)的。可以看出，樹(shù)由若干個(gè) \(\tt dfs\) 序連續(xù)的鏈條剖開(kāi)了。除了包含 \(1\) 的鏈，其他的鏈鏈頂?shù)母赣H都需提前記錄以消除后效性。對(duì)于每個(gè)節(jié)點(diǎn)，我們需要記錄的是位于其所在鏈上的每個(gè)滿足是一個(gè)鏈頂?shù)母赣H的節(jié)點(diǎn)（這個(gè)鏈頂 \(\tt dfs\) 序大于當(dāng)前節(jié)點(diǎn)，且深度不超過(guò)當(dāng)前節(jié)點(diǎn)），這一塊用狀壓實(shí)現(xiàn)。如果是一條鏈上長(zhǎng)了很多節(jié)點(diǎn)，復(fù)雜度就會(huì)上天，最高可達(dá) \(\mathcal O(2^\frac{n}{2})\)。

這種樹(shù)的剖分結(jié)構(gòu)影響復(fù)雜度的問(wèn)題，很自然能想到重鏈剖分，我們知道，重剖后一個(gè)節(jié)點(diǎn)到祖先的路徑上最多只有 \(\mathcal O(\log n)\) 條輕邊，嘗試著把這個(gè)應(yīng)用進(jìn)去。

考慮一個(gè)非常規(guī)的樹(shù)剖，記錄 \(\tt dfs\) 序時(shí)優(yōu)先往輕邊走。然后就可以發(fā)現(xiàn)每個(gè)節(jié)點(diǎn)需要額外記錄的僅有 \(\mathcal O(\log n)\) 個(gè)點(diǎn)。這樣子就不會(huì)出現(xiàn)一個(gè)節(jié)點(diǎn) \(u\) 的重兒子所在子樹(shù)往輕兒子中跳，只會(huì)從某個(gè)輕子樹(shù)跳到 \(u\) 的一個(gè)兒子。這樣的話，盡管 \(u\) 會(huì)被某個(gè)輕兒子記錄下來(lái)，但這一定是經(jīng)過(guò)了一條輕邊，字?jǐn)?shù)大小砍半了的，因此一個(gè)節(jié)點(diǎn)只會(huì)額外記錄除它自己的 \(\mathcal O(\log n)\) 個(gè)節(jié)點(diǎn)，狀壓復(fù)雜度為 \(\mathcal O(2^{\log n})=\mathcal O(n)\)。（真是奇了！）

于是我們改一下 dp：\(f_{i,S,j}\) 表示當(dāng)前轉(zhuǎn)移到 \(\tt dfs\) 序?yàn)?\(i\) 的節(jié)點(diǎn) \(u\)，\(u\) 記錄的節(jié)點(diǎn)和它自己的是否被選的狀態(tài)為 \(S\)，\(j\) 表示已選物品總體積 \(\sum a_k\) 的值。

然后轉(zhuǎn)移就簡(jiǎn)單了。復(fù)雜度降為 \(\mathcal O(n^2m)\) 輕松跑過(guò)。

幾個(gè)實(shí)現(xiàn) Hint：提前跳輕邊找到所有需記錄的節(jié)點(diǎn)，然后在轉(zhuǎn)移時(shí)建立映射方便 \(S\) 的轉(zhuǎn)移。使用二元結(jié)構(gòu)體來(lái)方便轉(zhuǎn)移 \(f,g\)，大大增強(qiáng)可讀性。

Click to find the code

#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 64, M = 10005, mod = 998244353, inf = 0xc0c0c0c0c0c0c0c0;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = x < y ? y : x; }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = x < y ? x : y; }
int n, m, a[N], b[N];
vector<int> G[N];
int sz[N], son[N], tp[N], fa[N];
void dfs1(int x, int fa) {
    sz[x] = 1, son[x] = 0;
    ::fa[x] = fa;
    for (auto y : G[x]) {
        if (y == fa) continue;
        dfs1(y, x);
        sz[x] += sz[y];
        if (!son[x] || sz[y] > sz[son[x]]) son[x] = y;
    }
}
int dfn[N], nfd[N], dfc;
void dfs2(int x, int top, int fa=0) {
    dfn[x] = ++dfc, tp[x] = top;
    nfd[dfc] = x;
    for (auto y : G[x]) {
        if (y == fa || y == son[x]) continue;
        dfs2(y, y, x);
    }
    if (son[x]) dfs2(son[x], top, x);
}
struct node {
    int v, c;
    inline friend node& operator += (node& a, const node& b) {
        if (a.v < b.v) a.v = b.v, a.c = b.c;
        else if (a.v == b.v) a.c += b.c;
        return a;
    }
} f[2][N][M];
vector<int> lin[N];
inline void solve() {
    cin >> n >> m;
    _f(i, 1, n) cin >> a[i] >> b[i], G[i].clear();
    _f(i, 2, n) {
        int u, v;
        cin >> u >> v;
        G[u].eb(v), G[v].eb(u);
    }
    dfc = 0;
    dfs1(1, 0), dfs2(1, 1);
    _f(i, 1, n) {
        lin[dfn[i]].clear();
        for (int u = i; u; u = fa[tp[u]]) lin[dfn[i]].eb(u);
    }
    memset(f[1], 0, sizeof(f[1]));
    f[1][0][0] = {0, 1}, f[1][1][a[nfd[1]]] = {b[nfd[1]], 1};
    _f(x, 2, n) {
        int s = lin[x-1].size(), t = lin[x].size(), p;
        static int mp[N];
        memset(mp, -1, sizeof(mp));
        memset(f[x&1], 0, sizeof(f[x&1]));
        for (int i = 0; i < s; ++i) {
            if (lin[x-1][i] == fa[nfd[x]]) p = i;
            for (int j = 0; j < t; ++j) if (lin[x-1][i] == lin[x][j]) mp[i] = j; 
        }
        for (int msk = 0; msk < 1<<s; ++msk) {
            int cur = 0;
            for (int i = 0; i < s; ++i) if ((msk>>i&1) && ~mp[i]) cur |= 1<<mp[i];
            _f(i, 0, m) if (f[x-1&1][msk][i].c) {
                f[x&1][cur][i] += f[x-1&1][msk][i];
                if (!(msk>>p&1) && i+a[nfd[x]] <= m)
                    f[x&1][cur|1][i+a[nfd[x]]] += {f[x-1&1][msk][i].v+b[nfd[x]], f[x-1&1][msk][i].c};
            }
        }
        
    }
    _f(i, 1, m) {
        node res={0,0};
        for (int msk = 0; msk < (1<<lin[n].size()); ++msk)
            res += f[n&1][msk][i];
        cout << res.c << (i == m ? '\n' : ' ');
    }
}
signed main() {
    FASTIO;
    int _; cin >> _;
    _f(_t, 1, _) {
        cout << "Case " << _t << ":\n";
        solve();
    }
    return 0;
}

posted @ 2025-08-27 21:42 goldspade 閱讀(12) 評(píng)論(0) 收藏舉報(bào)

刷新頁(yè)面返回頂部

loading...

gold-spade

[hdu6566]The Hanged Man

A. The Hanged Man on hdu

公告