from math import cos, sqrt, pi
import numpy as np

π = pi; N = 3
m = None # DCT矩陣
mt = None # IDCT矩陣，m的轉置
mc = None # "C"版本DCT矩陣
ms = None # string版DCT矩陣

ne = lambda a, b: not np.allclose(a, b, atol=1E-6)

def generate_dct_matrices():
  global m; global mt; global mc; global ms
  m = np.zeros((N, N))
  # [[0]*3]*3不對。[0]*3得[0,0,0]，再*3復制引用?而非創建獨立副本。修改任意一行會影響所有行；debug 1小時
  mc = [[0] * N for _ in range(N)]
  ms = [[0] * N for _ in range(N)]
  for k in range(N):
    for n in range(N):
      mc[k][n] = m[k,n] = cos((n + 0.5) * k * pi / N)
      ms[k][n] = f'cos({(n+0.5)*k}*π/{N})'
  m[0,:] *= sqrt(1/N)
  for n in range(N):
    mc[0][n] *= sqrt(1/N)
    ms[0][n] += f'*sqrt(1/N)'
  m[1:,:] *= sqrt(2/N)
  for k in range(1,N):
    for n in range(N):
      mc[k][n] *= sqrt(2/N)
      ms[k][n] += f'*sqrt(2/N)'
  mt = m.T
  if ne(m, mc): raise ValueError()

# x是一維數組，shape=(3,)，np將其視為?列向量?(3,1)
# 3x3 x 3x1 = 3x1. 720p是1280x720
dct  = lambda x: np.dot(m,  x)
idct = lambda y: np.dot(mt, y)
# So, dct和idct其實是一個函數

np.set_printoptions(
  suppress=True,  # 禁用科學計數法
  precision=3,    # 保留3位小數
  floatmode='fixed'  # 固定小數位數
)

generate_dct_matrices()

x = np.array([1.0, 2.0, 3.0]); print("輸入:", x)
y = dct(x); print("輸出:", y)
r = idct(y); print("重建:", r)
ee = np.eye(m.shape[0])
if ne(np.matmul(m, mt), ee): raise ValueError()
print()

y2 = [0] * N
for i in range(N):
  for j in range(N): y2[i] += mc[i][j] * x[j]
if ne(y, y2): raise ValueError()

y2 = [0] * N
for i in range(N):
  s = ''
  for j in range(N): s += f'{ms[i][j]}*{x[j]} + '
  s = s[:-3]
  y2[i] = eval(s)
  print(f'{[i]} {s} = {y2[i]:.3f}')
if ne(y, y2): raise ValueError()
print('')

print('恭喜，你（基本）明白DCT了！可M為啥是正交矩陣？！')

a = ms; b = np.array(ms).T; e = [[0] * N for _ in range(N)]
for i in range(N):
  for j in range(N):
    s = ''
    for k in range(N): s += f'{a[i][k]}*{b[k][j]} + '
    s = s[:-3]
    print(f'[{i},{j}] {s}')
    e[i][j] = eval(s)
if ne(e, ee): raise ValueError()
print()

print('如果用上復數（歐拉公式），就可以用等比數列求和公式了！！')

'''
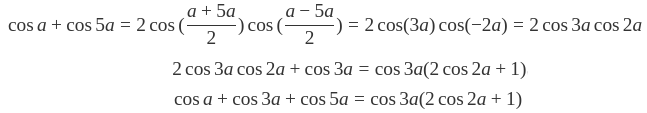
cos(1.0*π/3)*sqrt(2/N)*cos(1.0*π/3)*sqrt(2/N) + cos(3.0*π/3)*sqrt(2/N)*cos(3.0*π/3)*sqrt(2/N) + cos(5.0*π/3)*sqrt(2/N)*cos(5.0*π/3)*sqrt(2/N)
'''
from math import pi as π, cos
import numpy as np
α = π / 3
N = 3
print(f'{(2/N)*(cos(α)**2 + cos(3*α)**2 + cos(5*α)**2):.3f}')

δ_plural = 0; βs = np.linspace(0, 2*π, 100);
for β in βs:
  a = np.cos(β) + np.cos(3*β) + np.cos(5*β)
  b = np.cos(3*β) * (2*np.cos(2*β) + 1)
  δ = abs(a-b); δ_plural += δ
  if δ > 1E-6: raise ValueError()
  print(f'{δ_plural / βs.size:.3f}')

# cos2γ = (1 + cos2γ) / 2 = 1/2 + cos2γ/2
β = 2 * α
print(f'{(cos(3*β) * (2*cos(2*β) + 1) + 3/2) * 2/N:.3f}')