面向?qū)ο蟮谝粏卧偨Y

fishlife

寫在前面

? 除去小學時寫過的”文明小博客“之外，這是我第一次正兒八經(jīng)地寫一篇博文，希望能講清楚事情的同時寫出自己的風格。

? 第一單元的面向?qū)ο笞鳂I(yè)，總體而言完成的還算順利，因為有前幾屆學長學姐的博客參考，雖然我們的具體內(nèi)容有了較大差別，但還是能夠通過往屆的博客大致預測出下一次的作業(yè)風向，也就能更好地進行架構設計。但這其中也暴露出來一些問題需要重視。

本單元關鍵詞：初見與”叛逆“

? 初見很好理解，第一次接觸面向?qū)ο螅瑢ava語言的了解不多，雖然認真做完了pre，完成作業(yè)時還是會需要通過搜索引擎查找一些沒用過的java代碼操作，以擴充自己的java知識。

? 至于”叛逆“一詞，是這么解釋的：這次作業(yè)里，我的解決方法基本上就是指導書反著來，指導書不推薦的事情我全做了一遍，構成了自己的第一單元作業(yè)。這其中有很多的原因，但我后來發(fā)現(xiàn)，把這些不被看好的事物組合在一起，可能會構成另一條通向終點的道路。

分次作業(yè)分析

第一次作業(yè)

作業(yè)分析

? 第一次作業(yè)只需要對多項式進行化簡，相對而言架構設計比較簡單。我的思路是采用TreeMap存儲冪函數(shù)，Key為指數(shù)，Value為冪函數(shù)類PowerFun，常數(shù)則視為次數(shù)為0的冪函數(shù)，因為這樣可以將常數(shù)和冪函數(shù)統(tǒng)一，可以通過Key來判斷同類項，方便化簡。計算基本因子為\(ax^b\)。但在我思考計算化簡的思路時卻陷入了困境，我原本想采用遞歸下降的思路，所以我翻查了資料打算學會它，但是在當時的我眼里，遞歸下降更適合作為一個判定方法而非計算方法，打個比方就是這方法做判斷題好用但是做填空題不好使。終于，我在跟他鏖戰(zhàn)兩天后決定采取一個折衷的方法，即先用不推薦的后綴表達式做法，但是為后續(xù)的遞歸下降留好可以復用的類或模塊。所以在第一次作業(yè)里我使用的還是數(shù)據(jù)結構學到的老方法，但是向里面混入了一些面向?qū)ο蟮乃枷耄瑢Ρ磉_式組成成分進行分析封裝，最終誕生了這么一個“縫合怪”。

? 為了簡化計算，我設計了預處理器PreProgressor對輸入串作如下處理：

• 去除空白符
• 將重復符號等價替換，如“++”替換為“+”，“-++”替換為“-”。
• 將乘方符號等價替換，“**”替換為“^“
• 格式化，戰(zhàn)術補0，在所有單獨帶有符號的數(shù)后面補0，如“+1”改為“0+1”，上面兩步操作后，串內(nèi)僅可能存在[*^][+-]和([+-]兩種符號相連的情況，對這兩種情況特別處理。如“2*+3”改為“2*(0+3)”，“2^+3”改為“2^(0+3)”。

? 容易發(fā)現(xiàn)，上面一系列操作的最重要目的是防止污染符號棧，當連續(xù)兩個符號進棧后可能導致最后符號棧與計算因子棧無法匹配而出錯。

? 這次的化簡只涉及多項式，所以基本上直接做在了計算部分，主要為合并同類項。在輸出部分也通過專門編寫輸出方法以及改寫PowerFun的toString方法來進行輸出簡化，包括省略系數(shù)1，負項推遲輸出，x**2簡化為x*x等。

? 第一次作業(yè)的類圖如下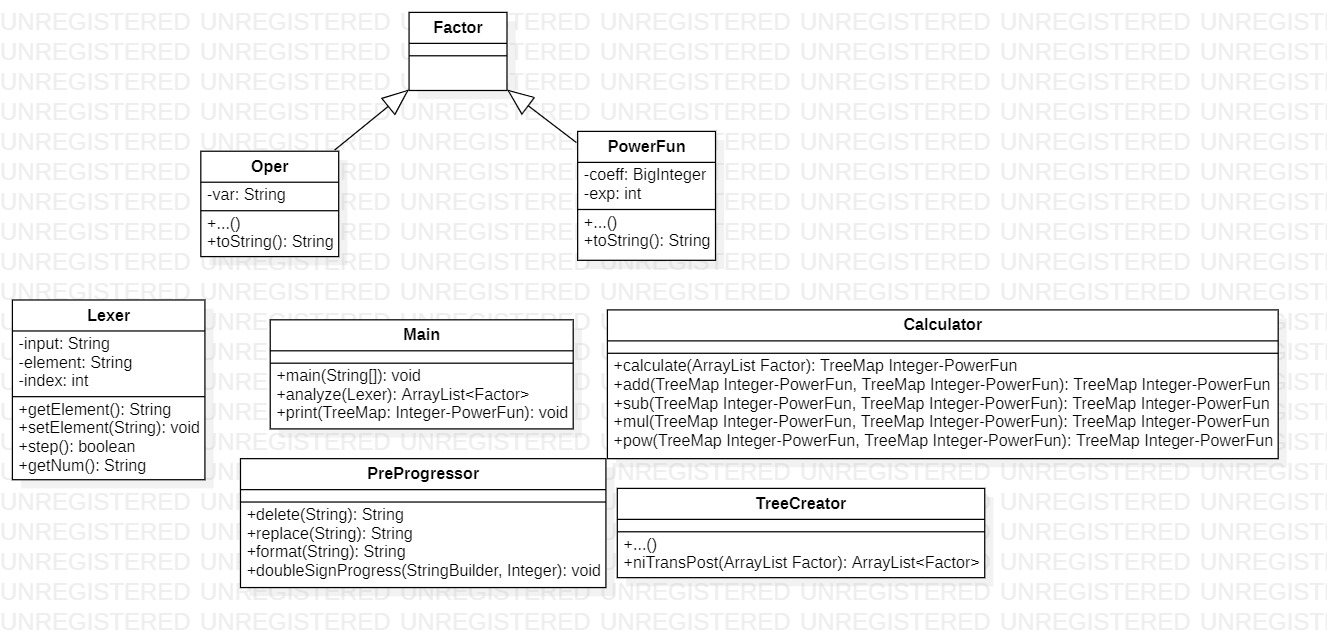

tips: 由于staruml以及其他規(guī)則的限制，此處部分容器類型的格式與一般格式不同，但均可輕易地辨識出原格式，對閱讀影響不大， 下同

? 類圖優(yōu)點是每個類各司其職，相互耦合性較小，且每個模塊均可單獨拿出來作為別的程序的組件使用。

? 缺點則是這種采用工具類的思想會使得類數(shù)量和類內(nèi)部方法的數(shù)量之間難以達到一個平衡。二者之間總有一個會在數(shù)量產(chǎn)生膨脹從而導致復雜度難以降低。并且每個類顯得過于分散，導致整體架構相對零散。

? 每個類的文字解釋如下：

類	解釋
Main	主類，包含主方法以及無法歸到某個工具類的方法
Factor	因子類
Oper	運算符類，用于封裝處理運算符
PowerFun	冪函數(shù)（帶系數(shù)）類，用于處理常數(shù)及冪函數(shù)
Lexer	分析器，用于從式子中按順序獲取運算符或冪函數(shù)
CalCulator	計算器，用于計算并化簡式子
PreProgressor	預處理器，用于對輸入串進行預處理，簡化后續(xù)計算操作
TreeCreator	樹生成器，更嚴謹講應該是后綴表達式生成器，用于生成后綴表達式。寫的時候一直想著遞歸下降重構，而重構后實際上生成的也是棵樹，故采用此名，后續(xù)由于這個原因未對名字作出修改，在此說明

復雜度分析

? 代碼量分析如下

? 可以看到總體上代碼量比較平均，Calculator類和Main類的代碼量相對偏多，這是由于calculator內(nèi)包含了所有的計算方法以及多項式化簡，而main類內(nèi)則有那些當時沒想好怎樣歸到工具類內(nèi)的方法，這些原因?qū)е麓a量偏多。

? 類復雜度分析如下：

Class	OCavg	OCmax	WMC
expressionclass.Factor	n/a	n/a	0
expressionclass.Oper	1	1	5
expressionclass.PowerFun	2.43	11	17
main.Main	4.67	9	14
util.Calculator	4.8	10	24
util.Lexer	1.38	3	11
util.PreProgressor	2.75	7	11
util.TreeCreator	5.33	8	16

? 可以看到比較復雜的類其實也是上面行數(shù)比較多的，而TreeCreator內(nèi)則是涉及到了中綴轉(zhuǎn)后綴的操作，所以復雜度較高。

? 方法復雜度分析如下

Method	CogC	ev(G)	iv(G)	v(G)
expressionclass.Oper.Oper()	0	1	1	1
expressionclass.Oper.Oper(String)	0	1	1	1
expressionclass.Oper.getVar()	0	1	1	1
expressionclass.Oper.setVar(String)	0	1	1	1
expressionclass.Oper.toString()	0	1	1	1
expressionclass.PowerFun.PowerFun()	0	1	1	1
expressionclass.PowerFun.PowerFun(BigInteger, int)	0	1	1	1
expressionclass.PowerFun.getCoeff()	0	1	1	1
expressionclass.PowerFun.getExp()	0	1	1	1
expressionclass.PowerFun.setCoeff(BigInteger)	0	1	1	1
expressionclass.PowerFun.setExp(int)	0	1	1	1
expressionclass.PowerFun.toString()	15	11	8	11
main.Main.analyze(Lexer)	5	1	4	4
main.Main.main(String[])	0	1	1	1
main.Main.print(TreeMap<Integer, PowerFun>)	13	6	8	9
util.Calculator.add(TreeMap<Integer, PowerFun>, TreeMap<Integer, PowerFun>)	4	1	3	3
util.Calculator.calculate(ArrayList<Factor>)	11	3	5	9
util.Calculator.mul(TreeMap<Integer, PowerFun>, TreeMap<Integer, PowerFun>)	12	1	6	6
util.Calculator.pow(TreeMap<Integer, PowerFun>, TreeMap<Integer, PowerFun>)	4	1	3	3
util.Calculator.sub(TreeMap<Integer, PowerFun>, TreeMap<Integer, PowerFun>)	4	1	3	3
util.Lexer.Lexer(String)	0	1	1	1
util.Lexer.getElement()	0	1	1	1
util.Lexer.getIndex()	0	1	1	1
util.Lexer.getInput()	0	1	1	1
util.Lexer.getNum()	2	1	3	3
util.Lexer.setElement(String)	0	1	1	1
util.Lexer.setIndex(int)	0	1	1	1
util.Lexer.step()	5	2	3	3
util.PreProgressor.delete(String)	0	1	1	1
util.PreProgressor.doubleSignProgress(StringBuilder, Integer)	15	6	8	8
util.PreProgressor.format(String)	2	1	1	2
util.PreProgressor.replace(String)	0	1	1	1
util.TreeCreator.niTransPost(ArrayList<Factor>)	21	6	11	11
util.TreeCreator.opCompare(String, String)	0	1	1	1
util.TreeCreator.opOrder(String)	1	6	1	6

? 總體上的復雜度不高，高復雜度方法（上文標粗的方法）基本上是由于分支過多導致的，比如PowerFun的toString復雜度主要來源于對化簡的分類討論，TreeCreator方法中的niTransPost方法則是因為對符號的優(yōu)先級判斷導致的復雜度上升。

bug分析（自己）

? 第一次作業(yè)的中強測以及互測中均未出現(xiàn)bug。

bug分析（他人）

? 在這次互測中，我主要采用的是隨機轟炸為主，精準打擊為輔的方法。最終查出一個別人的bug：結果為“-1”會輸出“-”，顯然這是化簡過頭了忘了考慮特殊情況。在我自己的程序中并未出現(xiàn)這種問題，因為在toString方法的編寫中已經(jīng)考慮到了這種情況。

第二次作業(yè)

作業(yè)分析

? 第二次作業(yè)增加了三角函數(shù)，自定義函數(shù)，求和函數(shù)，直接將難度抬升了一級。但很可惜的是，第二次作業(yè)時我依舊沒完全弄懂遞歸下降，只明白了”下降“但不知道怎么將分析好的因子”回歸“地計算回來。而繼續(xù)采用原架構的原因除了不懂遞歸下降且時間緊迫外，還有一個原因是我在第一次作業(yè)時已經(jīng)對第二次作業(yè)有了個基本的構想，這個在下文會詳談。

? 我的處理方法是這樣的

• 對三角函數(shù)，將其當成一個特殊的一元運算符，原串中”sin“替換為”s”，“cos”替換為“c“。由于sin，cos運算部分必定被一對括號括起來，所以在運算時，對括號處理完后再次判斷棧頂是否為三角運算符，若是則彈出后進入寫好的三角函數(shù)方法處理即可。

• 對自定義函數(shù)和求和函數(shù)，建立相應的類DiyFun和SumFun，并編寫對應的展開方法。展開策略是非常暴力的直接字符串替換，其間考慮到防止形參x和實參x的混用，在替換過程中采用了另一個不同于變量的字母當作占位符（本次作業(yè)中為w），最后統(tǒng)一將其換成x。為了防止出現(xiàn)暴力替換后運算優(yōu)先級變化，每個被替換的部分外圍用一對括號包圍。

• 計算部分的基礎因子更改為\(ax^b\prod_{i}sin^{c_i}(E_i)\prod_{j}cos^{d_j}(E_j)\)，三角函數(shù)專門建立三角函數(shù)類，里面包含計算因子。由于沒想到合適的key，所以采用HashSet存儲計算結果。

  加入了三角后，化簡的方法理論上有無數(shù)種，在這次作業(yè)中，保留了之前的多項式化簡，我經(jīng)過計算和統(tǒng)計分析（算了下期望），最終只采用了化簡效率最高的\(sin^2(E)+cos^2(E)=1\)。化簡部分寫在了AfterProgressor類里。

  本次作業(yè)類圖如下

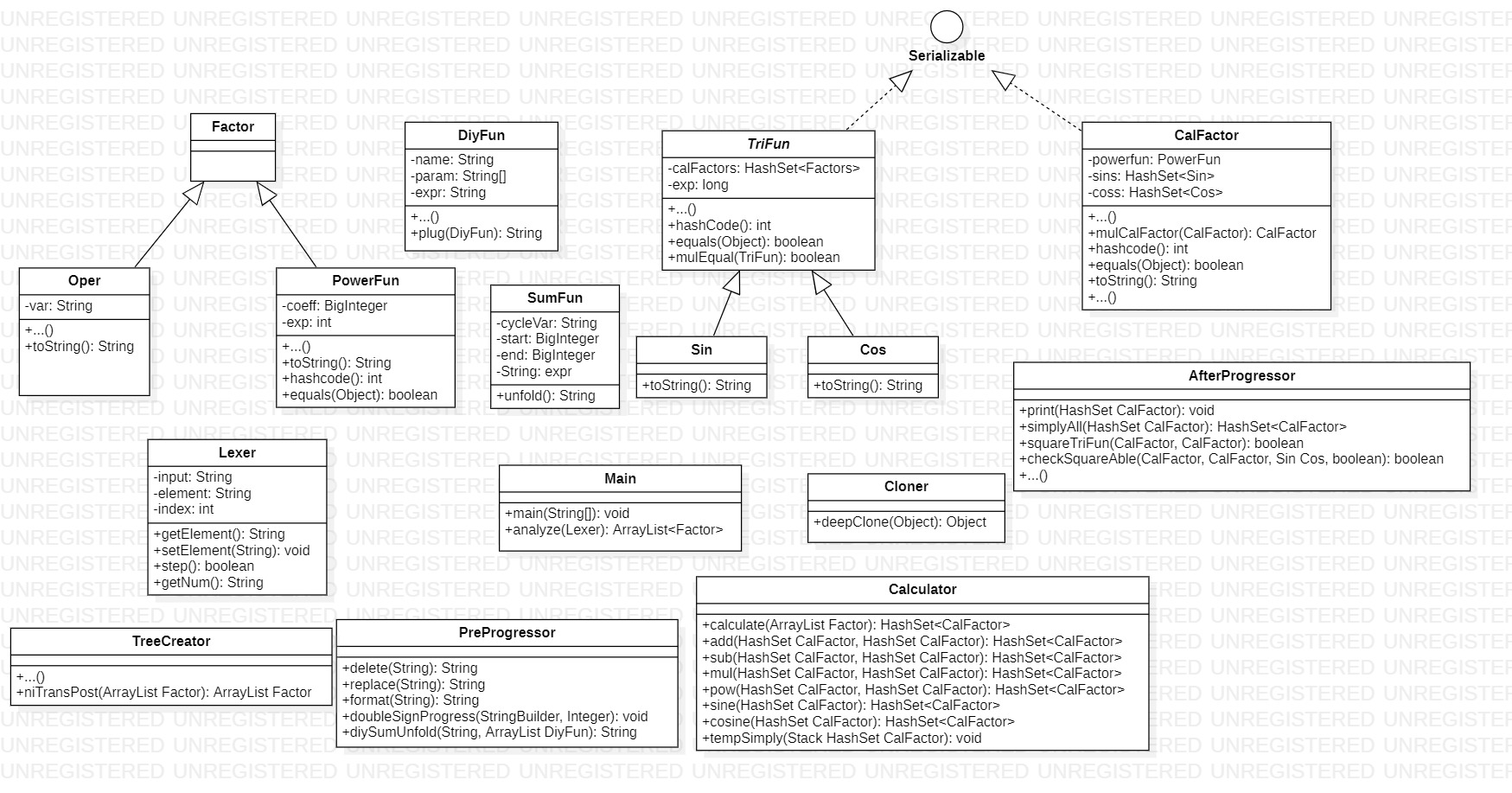
? 可以看到，這次的類圖比上次要復雜得多，但是模塊之間的耦合關系依舊很弱的優(yōu)勢依舊保留了下來，但是工具類越來越多也導致整個代碼的維護難度增大。而整體類圖也可以看到分成了兩個部分，左半部分是輸入與預處理部分，右半部分是計算與化簡部分，結構相對清晰。

? 本次對有變動的類文字解釋如下（參照第一次）

類	解釋
Main	主類，將print方法寫到了AfterProgressor中，簡化主類
PowerFun	冪函數(shù)類，增加對equals方法重寫用于化簡中同類項判斷
DiyFun	自定義函數(shù)類，對自定義函數(shù)的定義及調(diào)用進行封裝與處理
SumFun	求和函數(shù)類，對求和函數(shù)進行封裝與處理
TriFun	三角函數(shù)抽象類，對三角函數(shù)共性的部分進行封裝處理
Sin	正弦函數(shù)類，對正弦函數(shù)進行封裝處理
Cos	余弦函數(shù)類，對余弦函數(shù)進行封裝處理
CalFactor	計算因子類，將上面提到的基本計算因子進行封裝，便于計算與化簡
AfterProgressor	后處理器，對運算結果進行化簡與輸出
Cloner	克隆器，進行深克隆
PreProgressor	預處理器，增加對自定義函數(shù)與求和函數(shù)展開的方法
Calculator	計算器，增加三角函數(shù)計算與運算中的臨時化簡方法

復雜度分析

? 代碼量分析如下

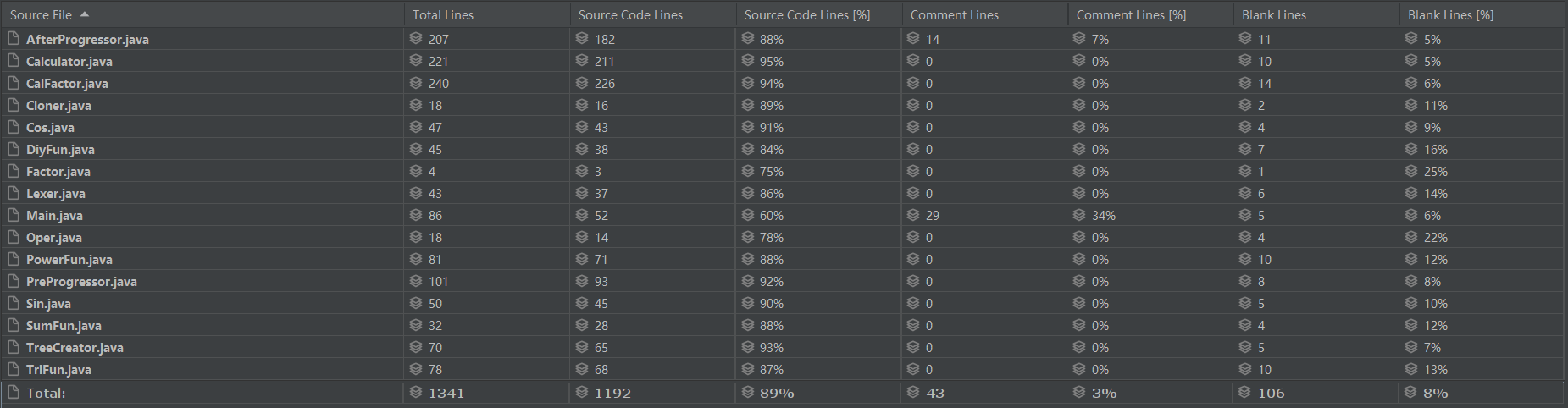
? 明顯地看到這次代碼量直接翻了一番，且代碼集中在計算與化簡部分。

? 類復雜度分析如下

Class	OCavg	OCmax	WMC
expressionclass.CalFactor	5.09	17	56
expressionclass.Cos	5	9	10
expressionclass.DiyFun	1.8	3	9
expressionclass.Factor	n/a	n/a	0
expressionclass.Oper	1	1	3
expressionclass.PowerFun	2.25	11	18
expressionclass.Sin	5.5	10	11
expressionclass.SumFun	2	3	4
expressionclass.TriFun	1.57	5	11
main.Main	3	4	6
util.AfterProgressor	6.29	11	44
util.Calculator	5	11	40
util.Cloner	1	1	1
util.Lexer	1.6	3	8
util.PreProgressor	4.6	12	23
util.TreeCreator	5.33	9	16

? 這次爆紅（表中為標粗）的類大幅增加，Calculator類在原本復雜度較高的情況下又增加了三角的計算，使復雜度進一步升高。而化簡部分為了化簡徹底，采用了循環(huán)暴力搜索的方法，這使得其作為一個新類復雜度卻很高。

? 方法復雜度分析如下

Method	CogC	ev(G)	iv(G)	v(G)
expressionclass.CalFactor.CalFactor()	0	1	1	1
expressionclass.CalFactor.CalFactor(PowerFun, HashSet<Sin>, HashSet<Cos>)	0	1	1	1
expressionclass.CalFactor.equals(Object)	29	9	13	13
expressionclass.CalFactor.getCoss()	0	1	1	1
expressionclass.CalFactor.getPowerFun()	0	1	1	1
expressionclass.CalFactor.getSins()	0	1	1	1
expressionclass.CalFactor.hashCode()	0	1	1	1
expressionclass.CalFactor.mulCalFactor(CalFactor)	22	6	11	11
expressionclass.CalFactor.selfClean()	20	1	14	14
expressionclass.CalFactor.toString()	0	1	1	1
expressionclass.CalFactor.toString(boolean)	47	3	19	22
expressionclass.Cos.Cos(HashSet<CalFactor>, long)	0	1	1	1
expressionclass.Cos.toString()	21	4	10	11
expressionclass.DiyFun.DiyFun(String)	2	1	3	3
expressionclass.DiyFun.getExpr()	0	1	1	1
expressionclass.DiyFun.getName()	0	1	1	1
expressionclass.DiyFun.getParam()	0	1	1	1
expressionclass.DiyFun.plug(DiyFun)	4	2	3	3
expressionclass.Oper.Oper(String)	0	1	1	1
expressionclass.Oper.getVar()	0	1	1	1
expressionclass.Oper.toString()	0	1	1	1
expressionclass.PowerFun.PowerFun(BigInteger, long)	0	1	1	1
expressionclass.PowerFun.equals(Object)	0	1	1	1
expressionclass.PowerFun.getCoeff()	0	1	1	1
expressionclass.PowerFun.getExp()	0	1	1	1
expressionclass.PowerFun.hashCode()	0	1	1	1
expressionclass.PowerFun.setCoeff(BigInteger)	0	1	1	1
expressionclass.PowerFun.setExp(long)	0	1	1	1
expressionclass.PowerFun.toString(boolean)	16	11	8	12
expressionclass.Sin.Sin(HashSet<CalFactor>, long)	0	1	1	1
expressionclass.Sin.toString()	22	5	10	12
expressionclass.SumFun.SumFun(String)	0	1	1	1
expressionclass.SumFun.unfold()	4	2	3	3
expressionclass.TriFun.equals(Object)	15	5	11	11
expressionclass.TriFun.getCalFactors()	0	1	1	1
expressionclass.TriFun.getExp()	0	1	1	1
expressionclass.TriFun.hashCode()	0	1	1	1
expressionclass.TriFun.mulEqual(TriFun)	0	1	1	1
expressionclass.TriFun.setCalFactors(HashSet<CalFactor>)	0	1	1	1
expressionclass.TriFun.setExp(long)	0	1	1	1
main.Main.analyze(Lexer)	5	1	4	4
main.Main.main(String[])	1	1	2	2
util.AfterProgressor.checkSquareAble(CalFactor, CalFactor, Sin, Cos, boolean)	12	6	6	6
util.AfterProgressor.print(HashSet<CalFactor>)	20	6	9	10
util.AfterProgressor.selfSimply(CalFactor)	27	6	11	11
util.AfterProgressor.setSelfClean(HashSet<CalFactor>)	1	1	2	2
util.AfterProgressor.setSimply(HashSet<CalFactor>)	3	1	3	3
util.AfterProgressor.simplyAll(HashSet<CalFactor>)	6	4	3	4
util.AfterProgressor.squareTriFun(CalFactor, CalFactor)	40	11	17	17
util.Calculator.add(HashSet<CalFactor>, HashSet<CalFactor>)	8	4	5	5
util.Calculator.calculate(ArrayList<Factor>)	14	5	6	10
util.Calculator.cosine(HashSet<CalFactor>)	5	3	3	4
util.Calculator.mul(HashSet<CalFactor>, HashSet<CalFactor>)	16	6	6	6
util.Calculator.pow(HashSet<CalFactor>, HashSet<CalFactor>)	1	1	2	2
util.Calculator.sine(HashSet<CalFactor>)	5	3	3	4
util.Calculator.sub(HashSet<CalFactor>, HashSet<CalFactor>)	8	4	5	5
util.Calculator.tempSimply(Stack<HashSet<CalFactor>)	2	1	3	3
util.Cloner.deepClone(Object)	0	1	1	1
util.Lexer.Lexer(String)	0	1	1	1
util.Lexer.getElement()	0	1	1	1
util.Lexer.getNum()	2	1	3	3
util.Lexer.setElement(String)	0	1	1	1
util.Lexer.step()	5	2	3	3
util.PreProgressor.delete(String)	0	1	1	1
util.PreProgressor.diySumUnfold(String, ArrayList<DiyFun>)	25	8	8	12
util.PreProgressor.doubleSignProgress(StringBuilder, Integer)	15	6	8	8
util.PreProgressor.format(String)	2	1	1	2
util.PreProgressor.replace(String)	0	1	1	1
util.TreeCreator.niTransPost(ArrayList<Factor>)	28	6	14	14
util.TreeCreator.opCompare(String, String)	0	1	1	1
util.TreeCreator.opOrder(String)	1	5	1	5

? 爆紅的方法依舊集中在計算和化簡部分，兩個部分均涉及到判斷同類項，涉及到CalFactor，PowerFun和TriFun三者之間equals方法的相互調(diào)用，導致復雜度急劇上升。

bug分析（自己）

? 本次作業(yè)的中強測中未出現(xiàn)bug，在互測中被測出一個bug，而這個bug的產(chǎn)生相當有意思。

? 可以發(fā)現(xiàn)，上文中的計算基本因子中，三角內(nèi)部我用的是\(E\)而不是\(x^n\)。實際上，這份作業(yè)已經(jīng)能夠支持三角內(nèi)帶表達式的情況了，所以我順便也將優(yōu)化一起做了，這個bug就來自”負項推遲出現(xiàn)“這一優(yōu)化，具體問題出現(xiàn)在TriFun抽象類的equals方法中。

? bug樣例：

0
sin(-1)

? 優(yōu)化原理是這樣的：遍歷三角內(nèi)所有CalFactor，找到第一個非負項輸出并用一個temp變量保存該項，之后在用增強for循環(huán)輸出，輸出到該項時則跳過。而本次作業(yè)中三角內(nèi)部僅可能出現(xiàn)一項，當該項為負時，temp沒有被更改，其仍為初始化時的值。而我原本采用的初始化是直接new一個新的對象，導致在后面輸出部分調(diào)用equals方法判斷是否和temp相同時，因為CalFactor的equals方法需要調(diào)用TriFun的equals方法，而此時temp的每項元素均為空，所以會報空指針異常導致RE。這個bug就算這次沒出現(xiàn)，在下次也會在內(nèi)部表達式每項均為負時出現(xiàn)。當然，這個bug被hack，歸根見底是測試沒做全面，上面這個樣例相當容易構造而且屬于一個基礎類。

? 修改方法也很簡單，將temp初始化為null，然后在判斷邏輯上加一句temp!=null即可。

? 觀察方法復雜度分析表可知，出bug的方法TriFun.equals圈復雜度偏高（11，大于10算偏高）。在所有方法中復雜度處于中上水平，可見復雜度和出bug的概率總體上還是呈正相關的，以后需要多加注意對復雜度的控制。

bug分析（他人）

? 本次作業(yè)由于失去了評測機，我主要是采用觀察別人的代碼構造樣例以及使用我自己用過的出過bug的樣例進行測試。顯然，直接上手看代碼的效率是相對較低的，于是我想到一個方法：把代碼下下來后看idea的warning信息，這部分信息經(jīng)常被忽視但卻點出了代碼中可能出現(xiàn)問題的地方。這樣我可以首先通過warning信息去有針對地找問題，極大提高效率。

? 本次作業(yè)中整個房間未發(fā)現(xiàn)除我以外其他人的bug。

第三次作業(yè)

作業(yè)分析

? 第三次作業(yè)增加了三角函數(shù)內(nèi)部因子嵌套和自定義函數(shù)多層調(diào)用，但在上文提到，第二次作業(yè)已經(jīng)支持三角函數(shù)內(nèi)嵌套因子，因此我只需要解決后面的問題即可。

? 而解決后面那個問題的方法很簡單：循環(huán)展開。

? 原串可一般表示為\(E_1f(f,g,h)E_2\)，其中f，g，h均為函數(shù)，第一次展開后會得到\(E_1(f,g,h)_fE_2\)，\((f,g,h)_f\)表示按f代入后的結果，再展開一次后則變?yōu)?span id="w0obha2h00" class="math inline">\(E_1(E_f,E_g,E_h)_fE_2\)此時如還存在自定義函數(shù)可繼續(xù)對其展開，由于調(diào)用層數(shù)有限，最終總是能展開到式子里沒有自定義函數(shù)，此時便完成了展開。求和函數(shù)的展開同理。
? tips：這種最原始的展開實際上無法處理求和函數(shù)內(nèi)套求和函數(shù)的情況，如需實現(xiàn)該需求則需要進行一定的修改，下文也會提到

? 所以除去新增的優(yōu)化部分，第二次作業(yè)到第三次作業(yè)的代碼增量很小。

? 第三次作業(yè)中新增的優(yōu)化主要有以下幾點，優(yōu)化的選擇基于期望收益與投入考慮。

• \(aE_1sin^2(E_2)+bE_1cos^2(E_2)=(a-b)E_1sin^2(E_2)+bE_1\)（增強版\(sin^2(E)+cos^2(E)=1\)）
• \(2sin(E)cos(E)=sin(2E)\)
• \(\pm(1-sin^{2}(E))=\pm cos^{2}E\)
• \(\pm(1-cos^{2}(E))=\pm sin^{2}E\)
• \(\pm(cos^2(E)-sin^2(E))=\pm cos(2E)\)
• \(sin(-E)=-sin(E)\)
• \(cos(-E)=cos(E)\)
  本次作業(yè)的類圖如下：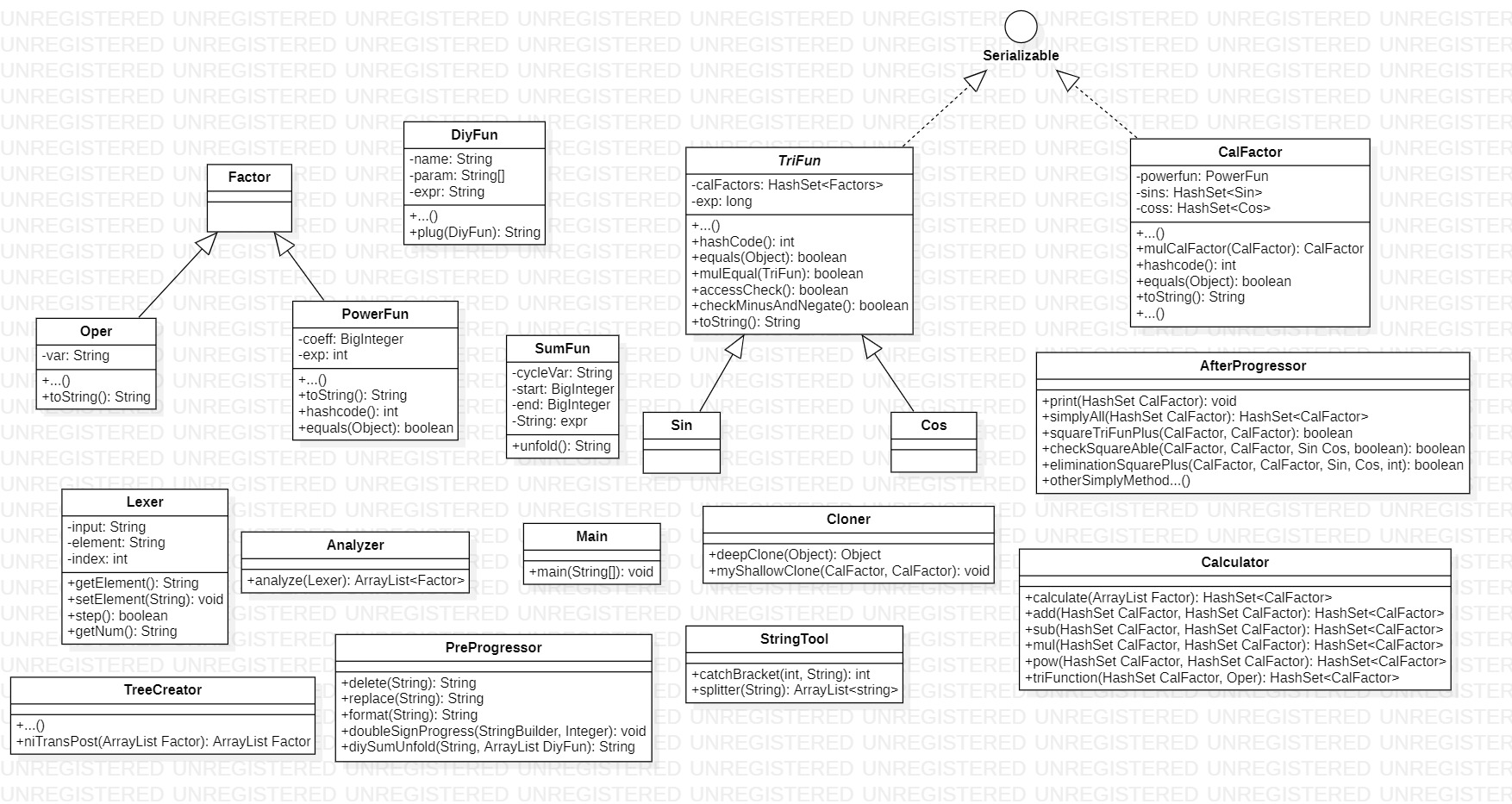

? 可以看到除了AfterProgressor加了一堆優(yōu)化方法之外，其他地方和第二次作業(yè)并無顯著差別，故不再贅述。當然這里應該檢討一下自己為了減少代碼量而把sin和cos的toString方法提到抽象類來，通過instance of來確定不同的部分如何輸出。實際上這么做個人認為是非常不好的，一旦三角種類增多，這邊if判斷就會跟著增多，復雜度一下就上來了，最好方式還是在每個三角函數(shù)類里單獨重寫toString方法，雖然重復代碼會很多，但這樣方便擴展。

? 本次作業(yè)中有變動的類的解釋如下（相較于第二次作業(yè)）：

類	解釋
AfterProgressor	后處理器，新增一大批化簡方法，具體功能見前文
Cloner	新增自己設計的淺克隆方法，用于計算與化簡中使用
Analyzer	分析器，與Lexer一起對輸入串進行分析
StringTool	字符串工具，將預處理，計算與化簡中常用的字符串處理方法單獨封裝成一個類，簡化代碼
TriFun	新增方法用于對三角內(nèi)式子進行符號化簡
其他變動類	主要是為了簡化代碼，對設計與正確性沒有影響，故不再贅述

復雜度分析

? 代碼量分析如下：

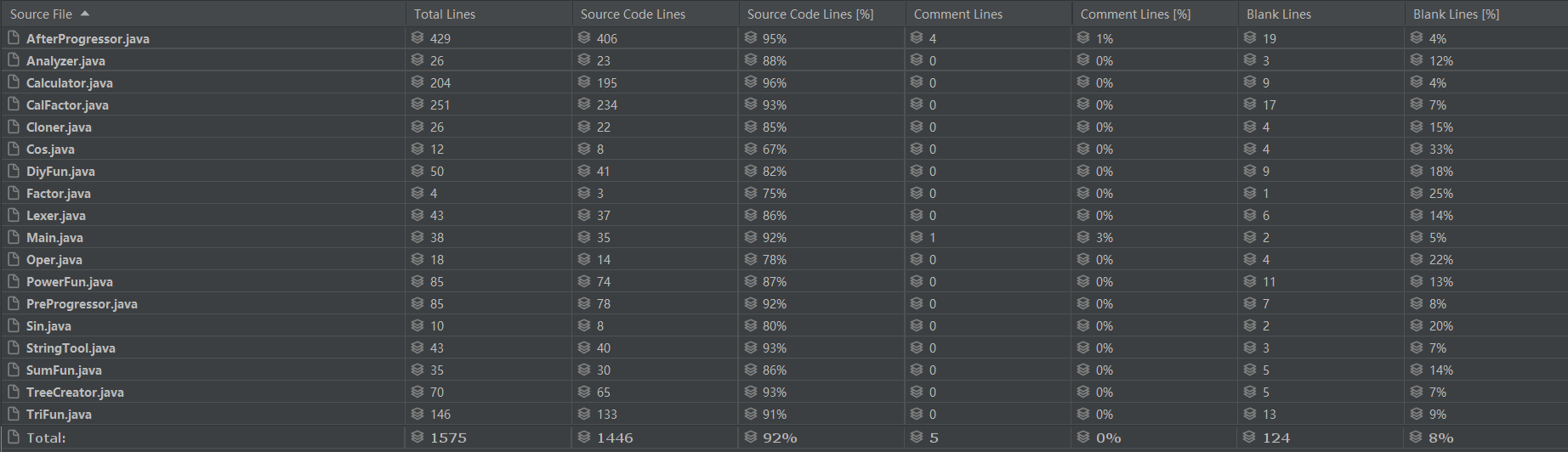
? 可以看到，除去AfterProgressor部分多出來的222行化簡代碼外，總代碼增量僅有12行，雖然我對代碼結構進行了一個優(yōu)化，減少了一部分代碼量，但估計真正的代碼增量不超過50行，所以這次迭代開發(fā)從完成任務的角度而言是比較輕松的。

? 類復雜度分析如下：

Class	OCavg	OCmax	WMC
expressionclass.CalFactor	4.21	17	59
expressionclass.Cos	1	1	1
expressionclass.DiyFun	1.8	3	9
expressionclass.Factor	n/a	n/a	0
expressionclass.Oper	1	1	3
expressionclass.PowerFun	2.11	11	19
expressionclass.Sin	1	1	1
expressionclass.SumFun	2	3	4
expressionclass.TriFun	3.2	14	32
main.Main	2	2	2
util.AfterProgressor	6.38	13	102
util.Analyzer	4	4	4
util.Calculator	5.83	10	35
util.Cloner	1	1	2
util.Lexer	1.6	3	8
util.PreProgressor	3.2	7	16
util.StringTool	5	5	10
util.TreeCreator	5.33	9	16

? 可以發(fā)現(xiàn)，除AfterProgressor外，其他類的復雜度較第二次作業(yè)并沒有很大的變動，這與這次改動主要是在優(yōu)化部分有很大關系。而由于將所有優(yōu)化方法全部集中在一個類里，導致AfterProgressor的WMC甚至達到了3位數(shù)。這是我們不愿看到的。實際上可以考慮把三角化簡做個分類，將化簡方法分散到不同的化簡類中來降低復雜度。

? 方法復雜度分析如下：

Method	CogC	ev(G)	iv(G)	v(G)
expressionclass.CalFactor.CalFactor()	0	1	1	1
expressionclass.CalFactor.CalFactor(PowerFun, HashSet<Sin>, HashSet<Cos>)	0	1	1	1
expressionclass.CalFactor.equals(Object)	27	9	12	12
expressionclass.CalFactor.getCoss()	0	1	1	1
expressionclass.CalFactor.getPowerFun()	0	1	1	1
expressionclass.CalFactor.getSins()	0	1	1	1
expressionclass.CalFactor.hashCode()	0	1	1	1
expressionclass.CalFactor.mulCalFactor(CalFactor)	22	6	11	11
expressionclass.CalFactor.selfClean()	20	1	14	14
expressionclass.CalFactor.setCoss(HashSet<Cos>)	0	1	1	1
expressionclass.CalFactor.setPowerFun(PowerFun)	0	1	1	1
expressionclass.CalFactor.setSins(HashSet<Sin>)	0	1	1	1
expressionclass.CalFactor.toString()	0	1	1	1
expressionclass.CalFactor.toString(boolean)	47	3	19	22
expressionclass.Cos.Cos(HashSet<CalFactor>, long)	0	1	1	1
expressionclass.DiyFun.DiyFun(String)	2	1	3	3
expressionclass.DiyFun.getExpr()	0	1	1	1
expressionclass.DiyFun.getName()	0	1	1	1
expressionclass.DiyFun.getParam()	0	1	1	1
expressionclass.DiyFun.plug(DiyFun)	4	2	3	3
expressionclass.Oper.Oper(String)	0	1	1	1
expressionclass.Oper.getVar()	0	1	1	1
expressionclass.Oper.toString()	0	1	1	1
expressionclass.PowerFun.PowerFun(BigInteger, long)	0	1	1	1
expressionclass.PowerFun.equals(Object)	0	1	1	1
expressionclass.PowerFun.getCoeff()	0	1	1	1
expressionclass.PowerFun.getExp()	0	1	1	1
expressionclass.PowerFun.hashCode()	0	1	1	1
expressionclass.PowerFun.setCoeff(BigInteger)	0	1	1	1
expressionclass.PowerFun.setExp(long)	0	1	1	1
expressionclass.PowerFun.toString()	0	1	1	1
expressionclass.PowerFun.toString(boolean)	16	11	8	12
expressionclass.Sin.Sin(HashSet<CalFactor>, long)	0	1	1	1
expressionclass.SumFun.SumFun(String)	0	1	1	1
expressionclass.SumFun.unfold()	4	2	3	3
expressionclass.TriFun.accessCheck()	3	2	5	5
expressionclass.TriFun.checkMinusAndNegate()	6	3	4	5
expressionclass.TriFun.equals(Object)	14	5	10	10
expressionclass.TriFun.getCalFactors()	0	1	1	1
expressionclass.TriFun.getExp()	0	1	1	1
expressionclass.TriFun.hashCode()	0	1	1	1
expressionclass.TriFun.mulEqual(TriFun)	0	1	1	1
expressionclass.TriFun.setCalFactors(HashSet<CalFactor>)	0	1	1	1
expressionclass.TriFun.setExp(long)	0	1	1	1
expressionclass.TriFun.toString()	29	5	10	16
main.Main.main(String[])	1	1	2	2
util.AfterProgressor.checkSquareMinusAble(CalFactor, CalFactor, Sin, Cos)	0	1	1	1
util.AfterProgressor.checkSquarePlusAble(CalFactor, CalFactor)	13	1	8	8
util.AfterProgressor.checkSquareSingleAble(CalFactor, CalFactor, TriFun, boolean)	20	6	8	8
util.AfterProgressor.eliminationSquarePlus(CalFactor, CalFactor, Sin, Cos, int)	18	6	9	9
util.AfterProgressor.oneOpSquareTriMerged(CalFactor, TriFun)	16	6	8	8
util.AfterProgressor.oneSubCosSquare(CalFactor, CalFactor)	20	1	13	13
util.AfterProgressor.oneSubSinSquare(CalFactor, CalFactor)	20	1	13	13
util.AfterProgressor.print(HashSet<CalFactor>)	20	6	9	10
util.AfterProgressor.selfSimply(CalFactor)	35	7	13	13
util.AfterProgressor.setSelfClean(HashSet<CalFactor>)	1	1	2	2
util.AfterProgressor.setSimply(HashSet<CalFactor>)	4	1	4	4
util.AfterProgressor.simplyAll(HashSet<CalFactor>)	24	13	9	13
util.AfterProgressor.simplyOneOpSquareTri(CalFactor, CalFactor, TriFun)	6	1	4	4
util.AfterProgressor.simplySquareTriFunMinus(CalFactor, CalFactor)	32	7	11	11
util.AfterProgressor.squareTriFunMinus(CalFactor, CalFactor)	4	1	5	5
util.AfterProgressor.squareTriFunPlus(CalFactor, CalFactor)	4	3	4	4
util.Analyzer.analyze(Lexer)	5	1	4	4
util.Calculator.add(HashSet<CalFactor>, HashSet<CalFactor>)	8	4	5	5
util.Calculator.calculate(ArrayList<Factor>)	14	4	6	10
util.Calculator.mul(HashSet<CalFactor>, HashSet<CalFactor>)	16	6	6	6
util.Calculator.pow(HashSet<CalFactor>, HashSet<CalFactor>)	9	1	6	6
util.Calculator.sub(HashSet<CalFactor>, HashSet<CalFactor>)	1	1	2	2
util.Calculator.triFunction(HashSet<CalFactor>, Oper)	15	3	6	7
util.Cloner.deepClone(Object)	0	1	1	1
util.Cloner.myShallowClone(CalFactor, CalFactor)	0	1	1	1
util.Lexer.Lexer(String)	0	1	1	1
util.Lexer.getElement()	0	1	1	1
util.Lexer.getNum()	2	1	3	3
util.Lexer.setElement(String)	0	1	1	1
util.Lexer.step()	5	2	3	3
util.PreProgressor.delete(String)	0	1	1	1
util.PreProgressor.diySumUnfold(String, ArrayList<DiyFun>)	8	1	5	5
util.PreProgressor.doubleSignProgress(StringBuilder, Integer)	15	6	8	8
util.PreProgressor.format(String)	2	1	1	2
util.PreProgressor.replace(String)	0	1	1	1
util.StringTool.catchBracket(int, String)	6	3	3	5
util.StringTool.spliter(String)	6	1	6	6
util.TreeCreator.niTransPost(ArrayList<Factor>)	28	6	14	14
util.TreeCreator.opCompare(String, String)	0	1	1	1
util.TreeCreator.opOrder(String)	1	5	1	5

? 同理，原有的方法復雜度并無太大變化，而新增的化簡方法每個復雜度都爆紅，與化簡統(tǒng)一采用暴力搜索方式有關，而這些新增的化簡方法都很復雜也導致了AfterProgressor的復雜度急速上升。

bug分析（自己）

? 本次中強測和互測中未發(fā)現(xiàn)bug，但是強測沒有把我的優(yōu)化完全跑出來，后面經(jīng)詢問發(fā)現(xiàn)，HashSet這種無序容器在不同的系統(tǒng)上運行結果可能不同，這點并未在指導書或其他官方材料中點出來，某種意義上這算一個小bug，我下次需要注意。

bug分析（他人）

? 本次互測我和上次一樣的策略，也是先看warning，再看代碼。同時采用了群友提供的一些數(shù)據(jù)。

? 本次互測中我未發(fā)現(xiàn)別人的bug，同房中有且僅有一個人被發(fā)現(xiàn)一個bug。

? bug樣例：

0
sin((sin(1)+cos(1)))

? 最終的輸出少掉了一層括號，原來是那個人化簡的部分出了問題。本次作業(yè)中三角函數(shù)內(nèi)為表達式時必須加一層括號，這點在TriFun的toString方法中我已經(jīng)考慮到了，僅有內(nèi)部為單獨一個冪函數(shù)或常數(shù)時才不加括號，否則加上外層括號，所以我的程序不存在這個問題。

綜合分析：化簡

? 三次作業(yè)里，化簡一直是一個可擴展性很強的任務。尤其是從第二次作業(yè)加入三角函數(shù)開始，化簡的方法就有無數(shù)種。而我從中挑選出了自認為最有效率的幾種。這里對三次作業(yè)中運用到的化簡思路進行一個統(tǒng)一，詳細的分析。

• 合并同類項：這項化簡貫穿了三次作業(yè)的化簡主線。這里的同類項指的是與計算基本因子相比的同類項。即第一次作業(yè)中的\(ax^b\)和第二、三次作業(yè)中的\(ax^b\prod_{i}sin^{c_i}(E_i)\prod_{j}cos^{d_j}(E_j)\)。當判斷為同類項時，則將他們的系數(shù)和指數(shù)進行處理。

  • 眾所周知，合并同類項和合并同類項不能一概而論，對不同的運算，同類項的概念可能是不一樣的，比如對加減法而言，\(a_1x^b\prod_{i}sin^{c_i}(E_i)\prod_{j}cos^{d_j}(E_j)\)和\(a_2x^b\prod_{i}sin^{c_i}(E_i)\prod_{j}cos^{d_j}(E_j)\)是同類項，指數(shù)和底數(shù)部分必須完全一致，而對乘法而言，\(a_1x^{b_1}\prod_{i}sin^{c_{i_1}}(E_i)\prod_{j}cos^{d_{j_1}}(E_j)\)和\(a_2x^{b_2}\prod_{i}sin^{c_{i_2}}(E_i)\prod_{j}cos^{d_{j_2}}(E_j)\)就算是同類項，只要求底數(shù)部分一致即可。所以，對不同運算的判斷同類項的方法是不一樣的，這也是為什么在TriFun類里面有equals和mulEquals兩種方法：equals用于判斷加減法同類項，而mulEquals用于判斷乘法的同類項，其算法是將原因子的各指數(shù)置1后調(diào)用equals方法。
  • 上面提到對原因子進行改動，而這個改動我們只希望發(fā)生在判斷部分，即不希望原式有任何變動，所以需要使用深克隆拷貝一份出來用于比對同類項，也就解釋了Cloner這個類產(chǎn)生的原因。
  • 關于深克隆，比較流行的做法是實現(xiàn)Clonable接口后一層一層調(diào)用clone方法，我覺得比較麻煩，就采用了另一種方法：序列化。雖然說這種方法不常用，但是序列化方法好處在于它接收和返回的參數(shù)都是Object，也就是說寫一個Cloner之后可以任意調(diào)用，對任何的類都可進行深克隆，復用性很高。

• 三角化簡：從第二次作業(yè)加入三角后，三角化簡部分就是八仙過海——各顯神通。如何從無數(shù)的三角公式里找到最高效的那個（些）是我在完成任務時一直在思考的。我最終采用的三角化簡策略是這樣的：

  • 總方針：能消去三角函數(shù)為先，無法消去三角函數(shù)則以效率為先。

  • 整個表達式中，最占位置的一定是三角函數(shù)，光禿禿的sin(x)就能占據(jù)6個字符，所以首要任務一定是消三角項。基于此產(chǎn)生的化簡策略有：

    • \(aE_1sin^2(E_2)+bE_1cos^2(E_2)=(a-b)E_1sin^2(E_2)+bE_1\)（增強版\(sin^2(E)+cos^2(E)=1\)）

    • \(\pm(cos^2(E)-sin^2(E))=\pm cos(2E)\)

    • \(2sin(E)cos(E)=sin(2E)\)：必須注意的是，該條的應用僅限于\(sin(E),cos(E)\)均為一次項時，否則無法達到消項的目的。甚至可能產(chǎn)生負優(yōu)化。一個經(jīng)典的例子如下

      0
      6*sin(x)**2*cos(x)**2
      

      使用二倍角公式化簡的結果是3*sin((2*x))*sin(x)*cos(x)，最終結果甚至比原來長，這顯然不是我們想看到的。可以看到此時二倍角公式并無法達到消三角項的作用，所以不應該進行化簡。

  • 無法消去三角項的情況下，涉及到的字符變動數(shù)一般很少，這時就需要衡量投入與產(chǎn)出來保證效率最大化（顯然這里效率不僅指程序效率，也指現(xiàn)實中的工作效率），基于此產(chǎn)生的化簡策略有

    • \(\pm(1-sin^{2}(E))=\pm cos^{2}E\)，\(\pm(1-cos^{2}(E))=\pm sin^{2}E\)：這兩條就是上面平方和公式的逆運算，整體思路相同，思考量小且代碼部分可復用。
    • \(sin(-E)=-sin(E)\)，\(cos(-E)=cos(E)\)：這兩項相當容易實現(xiàn)，后者直接少一個負號，前者可能在之后的負項提前優(yōu)化中發(fā)揮作用。

• 負項提前：將負項推遲輸出可將負號變成減號，這樣可能可以省去開頭一個符號，且易實現(xiàn)。

• 先計算后化簡還是先化簡后計算：實際上這兩個方法都無法做到完全最簡，對一部分式子先優(yōu)化更好，對另一部分式子則是先計算更好。一種比較暴力的策略是遍歷所有化簡順序輸出最短的那個，但這種說法極有可能導致超時。所以我采取的策略是先計算后化簡，但當出現(xiàn)三角運算符時先將已有式子進行化簡后放入三角中。

  • 這么做原因有二。一是三角函數(shù)內(nèi)部的式子幾乎不可能再被改變了，再不化簡就沒機會化簡了。二是化簡將三角內(nèi)部式子的形式進行了統(tǒng)一，方便之后對同類項的判斷以及化簡。

• 化簡策略整合：化簡策略使用順序按消去字符量由高到低排列；當任一化簡策略成功時，再次使用該策略，同時在所有策略執(zhí)行完畢時從頭開始再執(zhí)行一遍所有策略。

  • 第一點主要針對的情況是一個式子可能適用于多種化簡策略，但使用了其中一種之后就沒法再使用其他的，這時就應該使用化簡效率最高的策略進行化簡
  • 第二點主要針對的情況是一個式子使用了其中一種策略之后又符合另一種策略的條件，這樣便可以達到現(xiàn)有策略下的最簡。當然，這種算法帶來的一個巨大問題就是時間復雜度非常高。

宏觀架構分析

? 說實話，這三次作業(yè)架構的形成相當具有戲劇性。剛開始采用的臨時架構最后竟然一條路走到黑，還算不錯地完成了任務。架構迭代歷程及想法如下：
? 總體而言，架構采用了“輸入-運算-輸出”的三段式處理，三部分之間通過裝有各因子的容器進行數(shù)據(jù)傳輸。相互之間解耦合。

• 第一次作業(yè)：因不懂遞歸下降，采用后綴表達式的老方法。后綴表達式計算就是最基本的數(shù)據(jù)結構那套算法，在此不再贅述。同時為遞歸下降的重構留好了后路。PreProgressor，Calculator組件均可復用到遞歸下降中。而這套結構在構思時已經(jīng)想好了之后增加三角函數(shù)的處理方法：視為特殊運算符入棧。給自己做好了兩手準備。

  • 我們知道三角函數(shù)和一般運算符本質(zhì)上也是種映射關系。例如正弦函數(shù)和加號可定義為\(f(x)=sin(x)和g(x,y)=x+y\)，那既然一般的加減乘除能夠用后綴表達式進行計算，那么三角函數(shù)也可以使用后綴表達式進行計算，只需要調(diào)整一下符號棧和計算因子棧的彈出規(guī)則就行。三次作業(yè)的事實證明，這種做法是可行的。而且理論上，這種思想可以沿用到其他的初等函數(shù)甚至更復雜的函數(shù)中。

  • 可以發(fā)現(xiàn)第一次作業(yè)直接采用TreeMap<Integer, PowerFun>作為計算結果其實是對迭代不友好的，這種結構僅支持多項式，一旦公式復雜起來，就必須進行重構。所以從完成任務的角度看，這種寫法簡潔而高效，但從長遠來看，這增加了未來的工作量。

• 第二次作業(yè)：此時對遞歸下降一知半解，同時由于時間問題，重構可能會導致無法完成任務，于是決定沿用第一次的架構，實現(xiàn)之前的設想，同時對自定義函數(shù)和求和函數(shù)進行處理。

  • 對遞歸下降而言字符串處理可能不是個好辦法的原因有二：一是直接進行建模對函數(shù)進行遞歸更加直接，二是字符串展開會導致原來的遞歸深度進一步加深，不利于提速。但是對后綴表達式而言字符串替換則是比較好的，因為對表達式建模再用后綴去解，其效果和時間與直接展開后一起解決是一樣的，不存在遞歸深度的問題，而且后綴表達式處理多層冗余括號時僅涉及入棧退棧操作，相較于遞歸調(diào)用函數(shù)而言是很快的。所以采用了直接字符串替換的暴力方法。
  • 此時已經(jīng)大致猜到了第三次作業(yè)會在三角里放表達式，所以直接做出了三角函數(shù)放表達式的版本，而且在我的架構下，三角里面放什么東西對代碼量和思考量并不會造成太大影響，影響較大的則是分析出來的復雜度。

• 第三次作業(yè)：終于在舍友的幫助下搞懂了遞歸下降的“回歸”部分，但這次的任務要求在第二次作業(yè)時已完成了大半，沒有必要進行重構了。也就作罷，最終一條路走到黑。

  • 事實上，當時我想的是第三次作業(yè)是三角里套表達式加格式檢查。這樣我就可以在格式檢查部分實踐遞歸下降算法來檢驗一下我的學習成果（因為后綴表達式自身不帶格式檢查功能），但沒想到最后卻是三角套表達式加多層調(diào)用，這樣我沒辦法硬塞一個遞歸下降進去，而為了一個算法推倒已有的幾近完成的代碼顯然是不明智的，所以就繼續(xù)沿用了之前的架構，整個架構與指導書背道而馳。也正應了前文提到的關鍵詞“叛逆”。

? 從整體架構上分析，這次架構存在一個比較大的問題就是計算時間總體上偏長，雖然解決了遞歸下降問題，但一旦式子長起來，尤其是求和函數(shù)上下界差距大點，運算時間就會大幅上升。這個問題其實主要來源于暴力展開的層數(shù)多起來后，Calculator需要處理非常多的冗余括號，這樣便極大地浪費時間，但是加括號是為了保證運算優(yōu)先級不被打亂，保證正確性。在不動架構的情況下，只能先犧牲這部分時間。一個比較明顯的例子如下：

0
sum(i, 0, 220, (sin((i*x))**2+cos((i*x))**2))

? 這個式子基本上卡在公測數(shù)據(jù)長度的上限位置左右，用遞歸下降程序需要5s左右，而我的程序卻需要長達15s。

? 這次的架構在低耦合性上做得不錯，每個類單獨抽出來都可以作為一個模塊安插到別的程序去使用。但是卻沒有很好地貫徹OOP的思想。原因有二，其一是剛上手面向?qū)ο螅瑢ζ溥€不太熟悉，思維仍停留在面向過程，寫出的代碼中僅有對計算因子與解析因子的封裝上體現(xiàn)了面向?qū)ο蟮乃枷耄ぞ哳惖乃枷朐谶@實質(zhì)上是披著面向?qū)ο蟮钠さ拿嫦蜻^程。其二則是后綴表達式本身相較于遞歸下降而言，對表達式解析的粒度比較小，也更偏向于面向過程。不過從效果上看，這套架構還是很好地完成了任務。

? 在我的架構設計上，總是會“超前”設計或者預留一部分功能，并且從這三次作業(yè)的情況來看基本上每次都猜對了。雖然在現(xiàn)實的產(chǎn)品開發(fā)環(huán)境中，預留功能可以，但最好不要做超前設計防止客戶一個需求就把你之前的設計全給揚了。但是在面向?qū)ο笳n程中，我覺得這是可以的，因為超前設計肯定是建立在本周你時間充裕的情況下，這樣有利于我更靈活地調(diào)配自己的時間，并且本身代碼量不大，就算預測失誤代價也不大。所以在我的架構設計中總會看到一些本不屬于這次作業(yè)的設計。就以最后設計的終稿為例，實際上僅需稍加改動便可直接支持求和函數(shù)與自定義函數(shù)的互相嵌套，所以總體上，這套架構對需求變動的適應性和靈活性還是很好的。

總結心得

? 面向?qū)ο蟮牡谝粏卧诖艘嬌蟼€句號了。

? 在理論課上，我學到了基本的面向?qū)ο笏枷耄疫€能和同學們進行激烈的思想碰撞。OOP的思想確實是“只能意會，不能言傳”，光上課聽，不管老師講得多好，我能了解到的只有皮毛，只有親身實踐才能徹底明白OOP。這次作業(yè)內(nèi)面向?qū)ο蠛兔嫦蜻^程的混合其實挺好地反應了我的思想的轉(zhuǎn)變過程。雖然很多人都說面向?qū)ο蟾先祟惖乃伎紗栴}的方式，但私以為，面向過程和面向?qū)ο笾皇强创龁栴}的兩種方式，倒不存在誰更符合人類思想一說。而且在現(xiàn)在的程序中，兩種思想都有用武之地。而OO課的傾向自然是使用面向?qū)ο蟮乃枷耄@次作業(yè)算是面向?qū)ο笠粋€比較好的例子，他既能讓已經(jīng)了解面向?qū)ο蟮娜耸褂妹嫦驅(qū)ο笏枷敕浅Ａ鲿车赝瓿桑材苷疹櫟较裎乙粯記]辦法很快接受面向?qū)ο蟮娜擞妹嫦驅(qū)ο蠹用嫦蜻^程的“四不像”來完成，而且完成效果與前者并無二致。

? 在實踐作業(yè)中，我的架構思想得以實現(xiàn)。同時也體會到了迭代開發(fā)的一個簡要流程。而第一次實踐作業(yè)便給了我一個下馬威，當時的我就是呆坐在電腦前，看著遞歸下降的資料，毫無思路，最終只能說先用數(shù)據(jù)結構中學到的后綴表達式先挨過第一次作業(yè)再說，沒成想最后一條路走到黑。不得不說這次架構的形成充斥著諸多被逼走投無路后急中生智想出來的主意，例如改造棧彈出規(guī)則等，也算是從另一個角度學習了面向?qū)ο蠛蛷土暳藬?shù)據(jù)結構。

? 按照“千里眼”（就是往屆博客，我更喜歡這種叫法，以后可能沿用）的數(shù)據(jù)看，第一單元的代碼量比較大的（是否為最大有待考究），本單元作業(yè)最終實現(xiàn)時1500+的體量我也著實沒想到（我一直以為700-800行就能搞定了），但最終我完成了，最終完成的那一刻有一種無法言說的解脫感。

? 從第一單元OO課上我還學到一樣東西，就是時間管理以及懂得取舍。OO這門課神奇的地方在于它用各種規(guī)則想讓你把全部時間心甘情愿地花在他身上。顯然這是不可能的。生活不止眼前的OO，還有天邊的星光與手中的長槍。這次作業(yè)其實到最后最燒時間的地方就是做化簡，但是化簡除了依托的數(shù)學公式不同外，其余流程在不同的化簡之間并沒有很大的區(qū)別，而這次作業(yè)化簡可以無限地做下去。所以，從我的視角來看，從學習知識的角度上來看，過多做化簡是沒有太大意義的，甚至某種程度上違反了“不要重復造輪子”的原則。這就是我為什么化簡只做了上面這部分化簡的原因。OO教會了我舍去一些不必要的操作以換取更有價值的對時間的利用，提高整體的效率。

? 綜上，第一單元的面向?qū)ο笳n程我收獲很多。但顯然我的腳步不能在這停下，后面依舊有未知的挑戰(zhàn)在等著我，我將盡我所能去克服他們。