常見(jiàn)的組合優(yōu)化問(wèn)題有旅行商問(wèn)題和0-1背包問(wèn)題，組合優(yōu)化問(wèn)題由于其復(fù)雜度難以用窮舉法求得最優(yōu)解，但我們可以嘗試用低復(fù)雜度的算法求解滿意的局部最優(yōu)解。

什么是組合優(yōu)化問(wèn)題

定義

• 優(yōu)化問(wèn)題

  設(shè) \(x\) 是決策變量，\(D\) 是 \(x\) 的定義域，\(f(x)\) 是指標(biāo)函數(shù)，\(g(x)\) 是約束條件。則優(yōu)化問(wèn)題可以表示為求解滿足 \(g(x)\) 的 \(f(x)\) 最小值問(wèn)題。即：

  \[\min_{x\in D}(f(x)|g(x)) \]

• 組合優(yōu)化問(wèn)題

  如果在定義域 \(D\) 上，滿足約束條件 \(g(x)\) 的解的總數(shù)是有限的，則優(yōu)化問(wèn)題成為組合優(yōu)化問(wèn)題。

常見(jiàn)的組合優(yōu)化問(wèn)題

1. 旅行商問(wèn)題（TSP）

   一個(gè)商人去n個(gè)城市賣貨，從所在城市出發(fā)，每個(gè)城市去一次且僅去一次，并最后回到出發(fā)城市。問(wèn)如何安排才能
   使得商人走的路徑最短。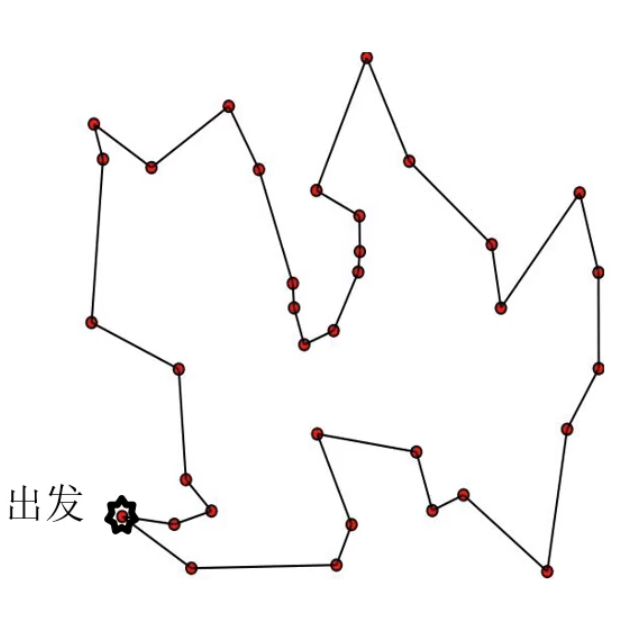

   

2. 0-1背包問(wèn)題

   給定一組物品，每種物品都有自己的重量和價(jià)格，在限定的總重量?jī)?nèi)，我們?nèi)绾芜x擇，才能使得物品的總價(jià)格最高。

   

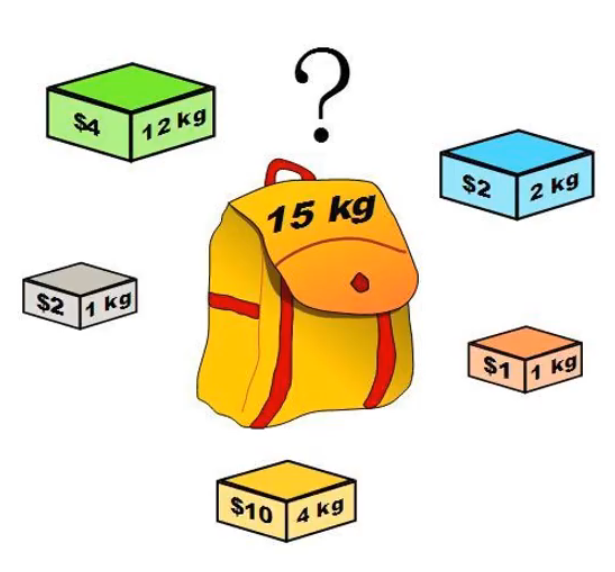
組合優(yōu)化問(wèn)題的實(shí)際意義

以旅行商問(wèn)題為例：

• 交通運(yùn)輸
• 飛機(jī)航班的安排
• 快遞員送快遞
• 校車的行駛路線
• 印刷電路板打孔

組合優(yōu)化問(wèn)題的難點(diǎn)

旅行商問(wèn)題可能的行走路線為 \(n!\) 個(gè)

復(fù)雜度是階乘級(jí)別的，這意味著使用窮舉法遍歷所有決策計(jì)算最優(yōu)解的思路是不可行的。

求解思路

引入隨機(jī)因素求解滿意解

• 最優(yōu)解與滿意解

  大多數(shù)時(shí)候組合優(yōu)化問(wèn)題求最優(yōu)解是十分困難的（復(fù)雜度很高）。如果退一步，只求相對(duì)較優(yōu)的“滿意解”，大多數(shù)時(shí)候可以滿足“滿意解符合實(shí)際問(wèn)題的需求”且“復(fù)雜度大大降低”。

• 引入隨機(jī)因素

  滿意解往往是局部最優(yōu)解，在設(shè)計(jì)算法的時(shí)候可以引入隨機(jī)因素，考慮數(shù)學(xué)期望，并在理論上認(rèn)為其可以收斂于較優(yōu)的局部最優(yōu)解。