樣本空間是隨機(jī)試驗(yàn)的所有可能結(jié)果，是樣本點(diǎn)的全體。 一個(gè)事件對(duì)應(yīng)于樣本空間中具有相應(yīng)特征的樣本點(diǎn)構(gòu)成的集合，是樣本空間的一個(gè)子集。 只有事件能討論概率，樣本點(diǎn)不討論概率。

第一章 隨機(jī)事件與概率

1.1 隨機(jī)事件

基本概念

隨機(jī)現(xiàn)象

• 確定性現(xiàn)象：在一定條件下必然出現(xiàn)的現(xiàn)象。
• 隨機(jī)現(xiàn)象：無(wú)法事先準(zhǔn)確預(yù)知其結(jié)果的現(xiàn)象。
• 統(tǒng)計(jì)規(guī)律性：隨機(jī)現(xiàn)象在大量重復(fù)觀察時(shí)所表現(xiàn)出來(lái)的量的規(guī)律性。
• 隨機(jī)試驗(yàn)：對(duì)隨機(jī)現(xiàn)象的觀察。簡(jiǎn)稱：試驗(yàn)。

隨機(jī)試驗(yàn)的特點(diǎn)：

1. 一定條件下可重復(fù)
2. 試驗(yàn)結(jié)果不止一個(gè)
3. 試驗(yàn)結(jié)果不可預(yù)測(cè)

樣本空間

• 樣本點(diǎn)：隨機(jī)試驗(yàn)的每一個(gè)可能結(jié)果。通常用\(\omega\)表示。
• 樣本空間：一個(gè)隨機(jī)事件所有樣本點(diǎn)的集合。通常用\(\Omega\)表示。

一個(gè)隨機(jī)試驗(yàn)將要出現(xiàn)的結(jié)果是不確定的，但其所有可能結(jié)果是明確的。

隨機(jī)事件

• 事件：一個(gè)指定的特征。

比如擲骰子時(shí)，“點(diǎn)數(shù)為偶數(shù)”這一指定特征就是一個(gè)事件。

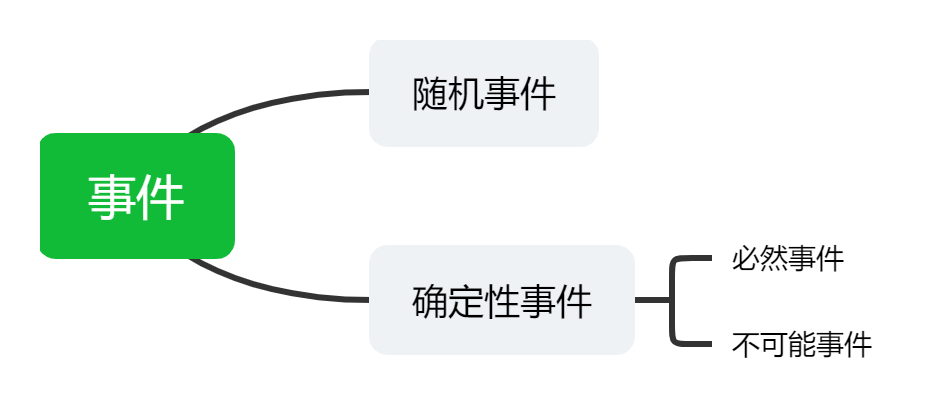
• 隨機(jī)事件：在隨機(jī)試驗(yàn)中可能發(fā)生也可能不發(fā)生的事件。
• 確定性事件：在試驗(yàn)之前就能夠準(zhǔn)確預(yù)知其是否發(fā)生的事件。
  • 必然事件：在試驗(yàn)中必然會(huì)發(fā)生的事件。
  • 不可能事件：在試驗(yàn)中一定不發(fā)生的事件。

通常將必然事件和不可能事件視為隨機(jī)事件的極端情形，并將隨機(jī)事件簡(jiǎn)稱為事件。

• 基本事件：最簡(jiǎn)單的，相對(duì)于試驗(yàn)?zāi)康牟荒茉俜?不必再分)的事件。

集合表示

• 樣本空間\(\Omega\)是隨機(jī)試驗(yàn)的所有可能結(jié)果，是樣本點(diǎn)\(\omega\)的全體。

• 一個(gè)事件對(duì)應(yīng)于\(\Omega\)中具有相應(yīng)特征的樣本點(diǎn)構(gòu)成的集合，是\(\Omega\)的一個(gè)子集。

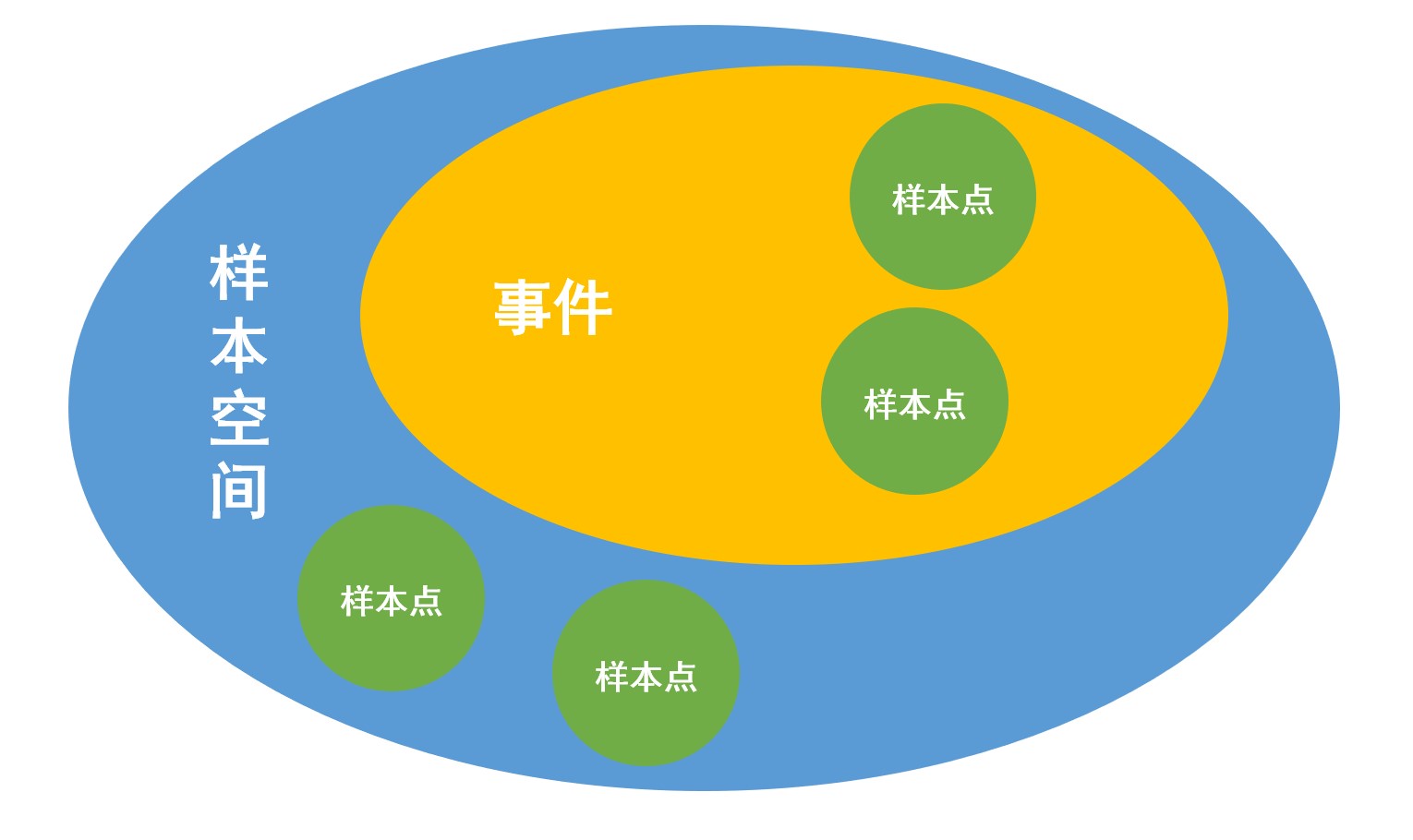
• \(\Omega\)表示必然事件，\(\varnothing\)作為空集表示不可能事件。
• 只有事件能討論概率，樣本點(diǎn)不討論概率。

例：

\(\omega\) 是樣本點(diǎn)

\(\{\omega \}\)是事件

事件的關(guān)系與運(yùn)算

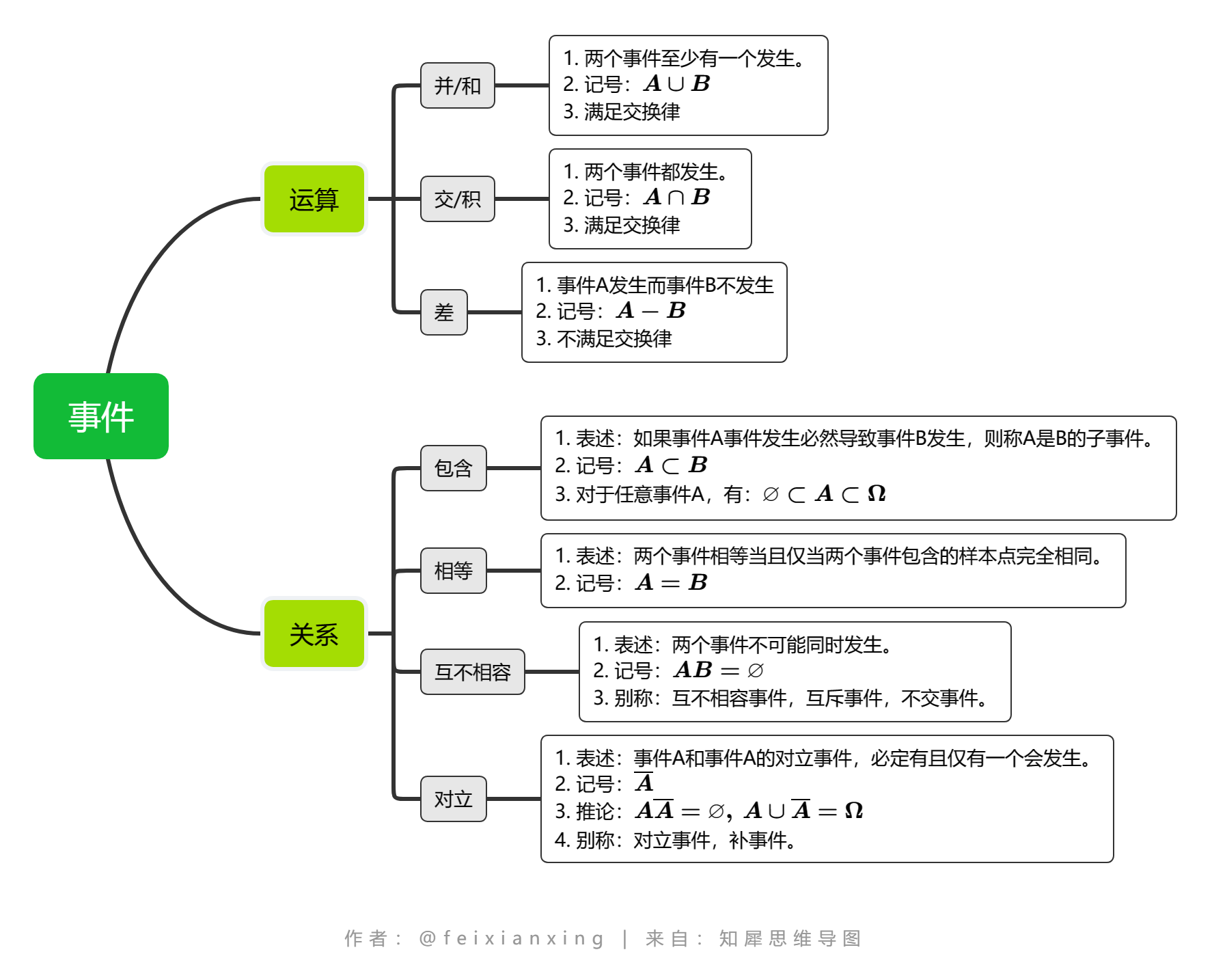
兩個(gè)事件之間的關(guān)系與運(yùn)算

有限個(gè)或可數(shù)個(gè)事件的并與交

有限個(gè)事件

• \(\bigcup\limits_{i=1}^nA_i\)表示若干個(gè)事件至少有一個(gè)會(huì)發(fā)生。
• \(\bigcap\limits_{i=1}^nA_i\)表示若干個(gè)事件都會(huì)發(fā)生。

可數(shù)個(gè)事件

可數(shù)(可列)用于描述無(wú)窮序列。

無(wú)限可列個(gè)：要求無(wú)窮大集合可以按某種規(guī)律排成一個(gè)序列。

可列的常見(jiàn)集合有：

1. 自然數(shù)：\(0,1,2,3,4,\cdots\)
2. 整數(shù)：\(0,\pm1,\pm2,\cdots\)
3. 有理數(shù)；

不可列的常見(jiàn)集合有：

1. 無(wú)理數(shù)；
2. 實(shí)數(shù)：無(wú)理數(shù)集不可列，因此實(shí)數(shù)集也不可列；
3. 直線點(diǎn)集

• \(\bigcup\limits_{i=1}^\infty A_i\)表示所有事件至少有一個(gè)會(huì)發(fā)生。
• \(\bigcap\limits_{i=1}^\infty A_i\)表示所有事件都會(huì)發(fā)生。

完備事件組

判定

若有限個(gè)或可數(shù)個(gè)事件，滿足兩兩互斥，且所有事件的并為\(\Omega\)，則稱這些事件是一個(gè)完備事件組.

性質(zhì)

若有限個(gè)或可數(shù)個(gè)事件是一個(gè)完備事件組，那么這些事件滿足兩兩互斥，且所有事件的并為\(\Omega\).

可以將完備事件組類比為拼圖，每一個(gè)事件是一塊碎片，拼湊起來(lái)剛剛好組成一整幅畫（即樣本空間\(\Omega\)）。

隨機(jī)事件的運(yùn)算律

隨機(jī)事件的運(yùn)算律是集合論知識(shí)的一種運(yùn)用。

交換律

• \(A\cup B = B\cup A\)
• \(A\cap B=B\cap A\)

結(jié)合律

• \((A\cup B)\cup C=A\cup (B\cup C) =A\cup B\cup C\)
• \((A\cap B)\cap C=A\cap (B\cap C) =A\cap B\cap C\)

分配律

• 第一分配律：\(A\cap (B\cup C)=(A\cap B)\cup(A\cap C)\)
• 第二分配律：\(A\cup (B\cap C)=(A\cup B)\cap(A\cup C)\)

自反律

• \(\overline{(\overline{A})}=A\)

德摩根律

• \(\overline{A\cup B}=\overline{A}\cap\overline{B}\)
• \(\overline{A\cap B}=\overline{A}\cup\overline{B}\)

常見(jiàn)記法

\(A,B,C\)是試驗(yàn)\(E\)的隨機(jī)事件

1. \(A\)發(fā)生：\(A\)

2. 只有\(A\)發(fā)生：\(A\overline{B} \overline{C}\)

3. \(A,B,C\)恰有一個(gè)發(fā)生：\(A\overline{B}\overline{C}+\overline{A}B\overline{C}+\overline{A}\overline{B}C\)

4. \(A,B,C\)同時(shí)發(fā)生：\(ABC\)

5. \(A,B,C\)至少一個(gè)發(fā)生：\(A+B+C\)

6. \(A,B,C\)至多一個(gè)發(fā)生：\(\overline{A}\overline{B}\overline{C}+A\overline{B}\overline{C}+\overline{A}B\overline{C}+\overline{A}\overline{B}C\)

7. 恰有兩個(gè)：\(AB\overline{C}+A\overline{B}C+\overline{A}BC\)

8. 至少兩個(gè)：\(AB+BC+AC\)

使用教材：
《概率論與數(shù)理統(tǒng)計(jì)》第四版 中國(guó)人民大學(xué) 龍永紅 主編 高等教育出版社