第三章 隨機向量

3.1 隨機向量的分布

隨機向量及其分布函數

概念

• \(X_1,X_2,\cdots,X_n\)是\(n\)個隨機向量，則\((X_1,X_2,\cdots,X_n)\)是一個\(n\)維隨機向量。
• \(n\)元函數\(F(x_1,x_2,\cdots,x_n)=P\{X_1\le x_1,X_2\le x_2,\cdots,X_n\le x_n\}\)為隨機向量\((X_1,X_2,\cdots,X_n)\)的分布函數。其中\(\{X_1\le x_1,X_2\le x_2,\cdots,X_n\le x_n\}\)表示\(\{X_1\le x_1\},\{X_2\le x_2\},\cdots,\{X_n\le x_n\}\)的交事件。

一般不會討論高維的向量，教材上大多是二維向量。

概率表示

性質

• \(0\le F(x,y)\le1\).

• \(F(x,y)\)關于\(x,y\)均單調、非降、右連續.

• 極限值：

  • \(F(-\infty,y)=\lim\limits_{x\to-\infty}F(x,y)=0\)
  • \(F(x,-\infty)=\lim\limits_{y\to-\infty}F(x,y)=0\)
  • \(F(-\infty,-\infty)=\lim\limits_{(x,y)\to(-\infty,-\infty)}F(x,y)=0\)
  • \(F(+\infty,+\infty)=\lim\limits_{(x,y)\to(+\infty,+\infty)}F(x,y)=1\)

• (一維)邊緣分布函數

  • \(F_X(x)=P\{X\le x\}=P\{X\le x,Y<+\infty\}=F(x,+\infty)\)

  • \(F_Y(y)=P\{Y\le y\}=F(+\infty,y)\)

  • 一般地，對于\(n\)維隨機向量的分布函數的邊緣分布函數為：

    \[F_i(x_i)=F(+\infty,\cdots,+\infty,x_i,+\infty,\cdots,+\infty),\quad i=1,2,\cdots,n \]

離散型隨機向量的概率分布

定義

如果二維隨機向量\((X,Y)\)只取有限個或可列個值，則稱\((X,Y)\)為二維離散型隨機向量。

其概率分布為：

也叫做\(X\)和\(Y\)的聯合概率分布。

性質

• \(p_{ij}\ge0,\quad i,j=1,2,\cdots;\)
• \(\sum\limits_i\sum\limits_jp_{ij}=1\).

概念

聯合概率分布表：以二維表格形式表示二維離散型隨機向量的概率分布。

邊緣概率分布：聯合概率分布的某一行或某一列的和。

連續型隨機向量的概率密度函數

定義

二維隨機向量\((X,Y)\)的分布函數為\(F(x,y)\)，如果存在一個非負可積的二元函數\(f(x,y)\)，使得對任意實向量\((x,y)\)，有

則稱\((X,Y)\)為二維連續型隨機向量，并稱\(f(x,y)\)為\((X,Y)\)的概率密度函數，或\(X\)和\(Y\)的聯合密度函數。

性質

• \(f(x,y)\ge0\)

• \(\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)\mathrmw0obha2h00x\mathrmw0obha2h00y=1\)

• 若\(D\)是平面上的一個區域，則\(P\{(X,Y)\in D\}=\iint\limits_Df(x,y)\mathrmw0obha2h00x\mathrmw0obha2h00y\)

• 邊緣分布函數

  \[\begin{align*} F_X(x) &= P\{X\le x\}=P\{X\le x,Y\le+\infty\}\\ &= \int_{-\infty}^x\int_{-\infty}^{+\infty}f(s,t)\mathrmw0obha2h00s\mathrmw0obha2h00t \\ &= \int_{-\infty}^x \left[ \int_{-\infty}^{+\infty}f(s,t)\mathrmw0obha2h00t \right] \mathrmw0obha2h00s. \end{align*} \]

• 邊緣密度函數

  \[f_X(x)=\int_{-\infty}^{+\infty}f(x,y)\mathrmw0obha2h00y \\ f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)\mathrmw0obha2h00x \\ \]

均勻分布

如果一個二維隨機向量\((X,Y)\)以

為密度函數，則稱\((X,Y)\)服從區域\(G\)上的均勻分布。

圖像

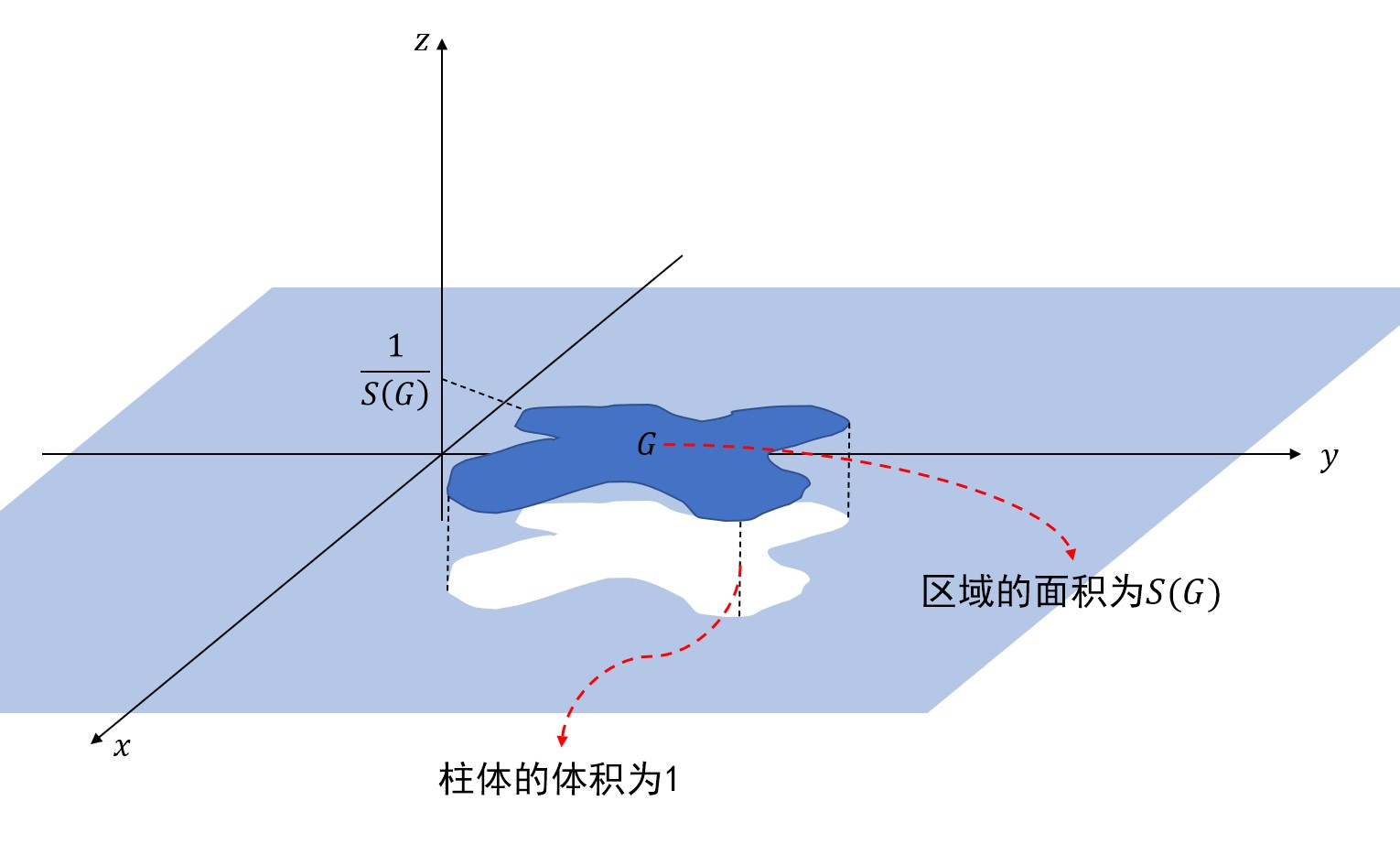
平面區域上的均勻分布實質就是平面區域上的幾何概型。

二元正態分布

定義

設隨機向量\((X,Y)\)的密度函數為

其中\(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho\)均為參數，且\(\sigma_1>0,\sigma_2>0,|\rho|<1\)，則稱\((X,Y)\)服從參數為\((\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho)\)的二元正態分布，記作\((X,Y)\sim N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho)\).

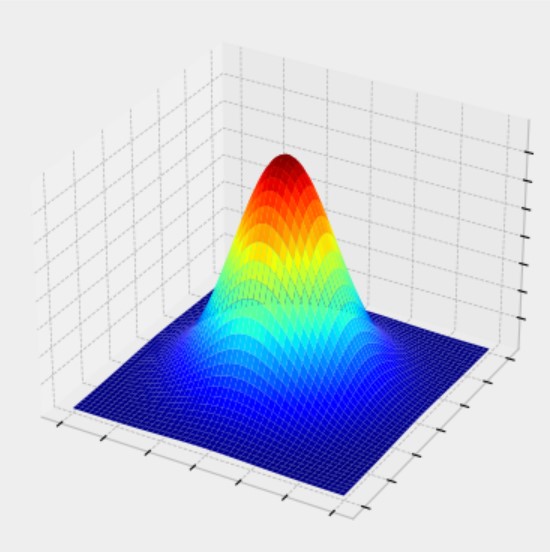
性質

• 二元正態分布以\((\mu_1,\mu_2)\)為中心，中心附近具有較高密度，離中心越遠，密度越小。

• 邊緣密度函數

  • \(\varphi_X(x)=\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}}\)
  • \(\varphi_Y(y)=\frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{(x-\mu_2)^2}{2\sigma_2^2}}\)
  • \(X\sim N(\mu_1,\sigma_1^2),\ Y\sim N(\mu_2,\sigma_2^2)\)

• 參數\(\rho\)是隨機變量\(X,Y\)的相關系數，\(\rho=0\)表示\(X,Y\)相互獨立，此時對于任何\((x,y)\)，有

  \[\varphi(x,y)=\varphi_X(x)\varphi_Y(y) \]

注：

1. 二元正態分布的邊緣分布只有前4個參數確定，因此對于只有參數\(\rho\)不同的二元正態分布，它們的邊緣分布是一致的。
2. 只有\(X\)和\(Y\)的邊緣分布不能唯一確定二元正態分布，還需要明確的參數\(\rho\).
3. 兩個邊緣分布為正態分布的二位隨機向量不一定服從二元正態分布。

使用教材：
《概率論與數理統計》第四版 中國人民大學 龍永紅 主編 高等教育出版社