3.3 隨機向量的函數的分布與數學期望

離散型隨機向量的函數的分布

定義

• 離散型隨機向量\((X,Y)\)的分布為

  \[P\{X=x_i,Y=y_j\}=p_{ij},\quad i,j=1,2,\cdots, \]

• 隨機向量的函數為\(Z=g(X,Y)\)，記其所有可能取值為\(z_k(k=1,2,\cdots)\)

• \(Z\)的概率分布為

  \[P\{Z=z_k\}=P\{g(X,Y)=z_k\}=\sum\limits_{g(x_i,y_j)=z_k}P\{X=x_i,Y=y_j\} \]

解題步驟

1. 繪制隨機向量\((X,Y)\)的概率分布表。
2. 計算出\(Z\)的所有可能取值。
3. 將概率分布表中\(z_k=g(x_i,y_j)\)的值相同的項合并相加，即得\(Z\)的概率分布。

泊松分布的再生性

如果\(X,Y\)相互獨立且\(X\sim P(\lambda_1),Y\sim P(\lambda_2)\)，則對于\(Z=X+Y\)，有\(Z\sim P(\lambda_1+\lambda_2)\).

連續型隨機向量的函數的分布

定義

設\((X,Y)\)是二維連續型隨機向量，其概率密度函數為\(f(x,y)\)，函數\(Z=g(X,Y)\)，則分布函數

其中\(D_z=\{(x,y)|g(x,y)\le z\}\).

而密度函數\(f_Z(z)=F'_Z(z)\).

計算分布函數和密度函數的關鍵在于：

1. 找出區域\(D_z\).
2. 計算二重積分\(\iint\limits_{D_z}f(x,y)\mathrmw0obha2h00x\mathrmw0obha2h00y\)

卷積公式

公式

如果\(X,Y\)相互獨立且\(Z=X+Y\)，則\(Z\)的密度函數為

這里的積分運算稱為函數\(f_X(x)\)與\(f_Y(y)\)的卷積，記作\(f_X*f_Y(z)\).

上述公式可以記為：

說明

卷積是一種應用很廣泛的運算，這里的卷積公式是兩個函數卷積生成一個新函數的一種運算。

關于卷積的相關視頻：【官方雙語】那么……什么是卷積？

公式推導過程

引例題目

設\((X,Y)\)的聯合密度函數為\(f(x,y)\)，\(X,Y\)相互獨立，求\(Z=X+Y\)的密度函數。

推導過程

首先

二重積分相關知識點：

• 計算二重積分可以化為兩次積分運算。
• 在直角坐標系中，有X型和Y型兩種，區別是對于區域的掃描方式。

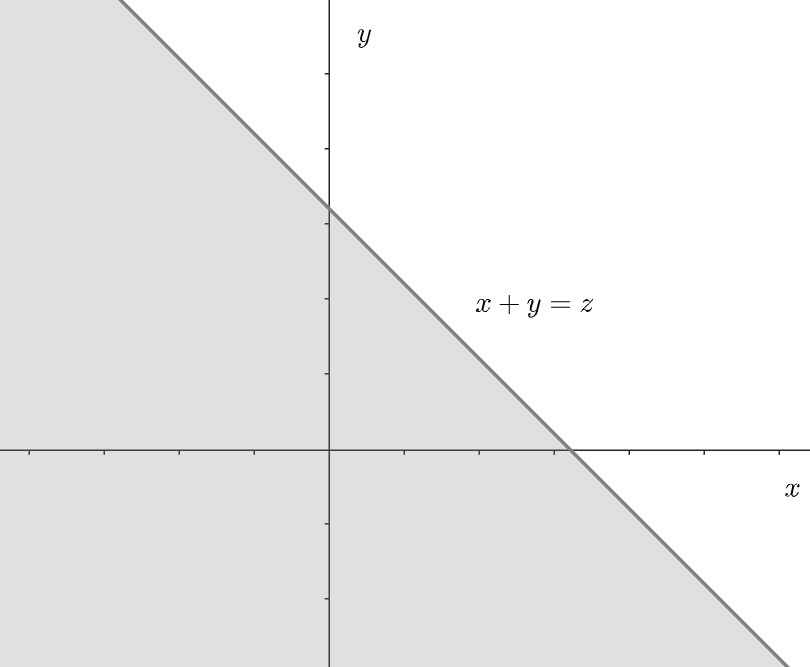
分界線\(x+y=z\)化為\(y=z-x\).

對于上述二重積分采用X型，區域的\(x\)從\(-\infty\)到\(+\infty\)，\(y\)從\(-\infty\)到直線\(y=z-x\)，所以

為了使區域更加規范，這里采用換元法，令\(t=x+y\)，將\(y\)替換為\(t\)，上述積分的\(x\)部分不變，\(y\)部分內：\(y\)為變量，\(x\)為常量，\(t=x+y\)為變量。

積分換元時，需要注意3個部分：

1. 積分上下限的改變
2. 被積函數的改變
3. 積分變量的改變

• 當\(y\to-\infty\)時，\(t\to-\infty\)；當\(y= z-x\)時，\(t=x+y=x+(z-x)=z\).

• 因為\(y=t-x\)，所以\(f(x,y)=f(x,t-x)\).

• \(\mathrmw0obha2h00y=\mathrmw0obha2h00(t-x)=\mathrmw0obha2h00t\).（這里的 \(x\) 是常數，可以直接去掉）

因此

注意：此時是二重積分的\(X\)型表示。

換元后的區域為\(t\le z\).

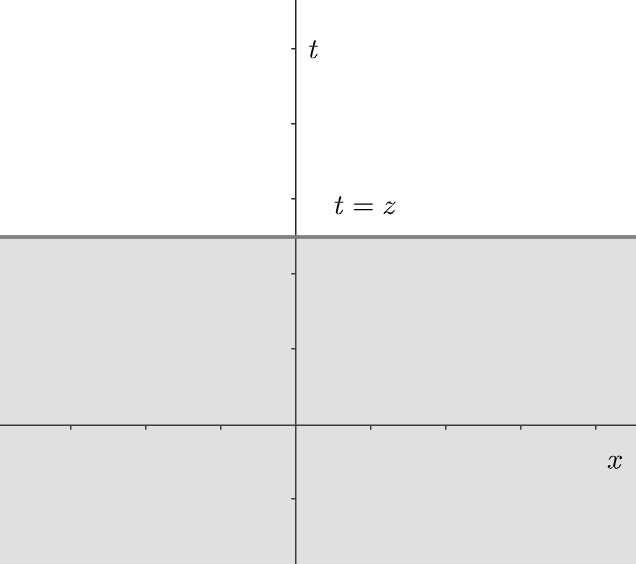
此時，將上述二重積分的\(X\)型表示轉換為\(Y\)型表示。

一般來說，二重積分\(X\)型\(Y\)型的互相轉換是會導致積分上下限發生改變的，這里因為之前進行了換元，將積分區域轉換為了簡單的“矩形”，因此積分上下限與原來一樣，只是積分次序發生改變。事實上，只要積分區域是“矩形”，就可以隨便改變積分次序而不用修改積分上下限。

推導到這里，有：

又因為\(f_Z(z)=F_Z'(z)\)，根據變上限積分求導公式，有：

這里的\(f\)是\(X,Y\)的密度函數，根據上述前提條件：\(X,Y\)相互獨立，有：

根據對稱性，同樣的思路可以推導出\(f_Z(z)=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)\mathrmw0obha2h00y\).

推導完畢.

正態分布的再生性

若\(X,Y\)相互獨立且分別服從正態分布\(N(\mu_1,\sigma_1^2)\)和\(N(\mu_2,\sigma_2^2)\)，則其任意非零線性組合仍服從正態分布，且

其中\(a,b\)不全為0。

這一結論可以推廣到\(n\)個隨機變量的情形。

最大值與最小值

\(X,Y\)相互獨立，令\(M=\max\{X,Y\}\)，\(N=\min\{X,Y\}\)，則

• \(M\)的分布函數為：\(F_M(z)=F_X(z)F_Y(z)\).
• \(M\)的密度函數為：\(f_M(z)=f_X(z)F_Y(z)+F_X(z)f_Y(z)\).
• \(N\)的分布函數為：\(F_N(z)=1-\left[1-F_X(z)\right]\left[1-F_Y(z)\right]\).
• \(N\)的密度函數為：\(f_N(z)=f_X(z)\left[1-F_Y(z)\right]+f_Y(z)\left[1-F_X(z)\right]\)

隨機向量的函數的數學期望

設\(Z=g(X,Y)\)，

• 對于離散型，有\(EZ=\sum\limits_i\sum\limits_jg(x_i,y_j)p_{ij}\)

• 對于連續型，有\(EZ=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)\mathrmw0obha2h00x\mathrmw0obha2h00y\)

數學期望的進一步性質

1. 如果隨機變量\(X,Y\)的數學期望都存在，則\(E(X+Y)\)存在，且\(E(X+Y)=EX+EY\).
2. 如果\(X,Y\)相互獨立且數學期望均存在，則\(E(XY)\)存在，且\(E(XY)=EX\cdot EY\).

使用教材：
《概率論與數理統計》第四版 中國人民大學 龍永紅 主編 高等教育出版社