1.4 條件概率

條件概率

• 樣本空間\(\Omega\)
• 事件\(A,B\)
• \(P(B)>0\)

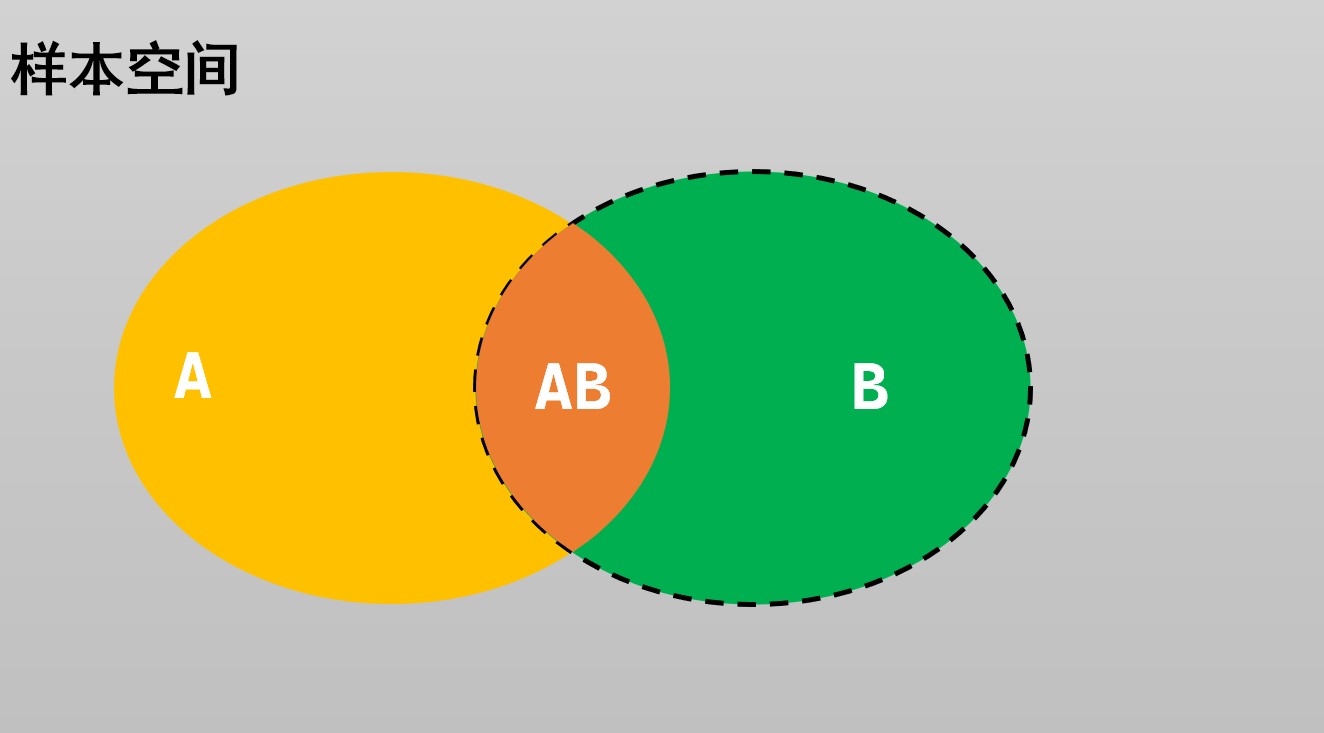
在事件\(B\)已經(jīng)發(fā)生的前提條件下，事件\(A\)發(fā)生的概率稱為A對(duì)B的條件概率：\(P(A|B)\).

通常，\(P(A)\)為無(wú)條件概率，對(duì)應(yīng)的樣本空間為\(\Omega\)。

而條件概率\(P(A|B)\)對(duì)應(yīng)的樣本空間為\(B\)，或者記為\(\Omega_B\).

所以：

乘法公式

根據(jù)\(P(A|B)=\frac{P(AB)}{P(B)}\)可以推導(dǎo)出：

1. \(P(AB)=P(A)P(B|A)\)
2. \(P(AB)=P(B)P(A|B)\)

其中要求\(P(A)>0,\ P(B)>0\).

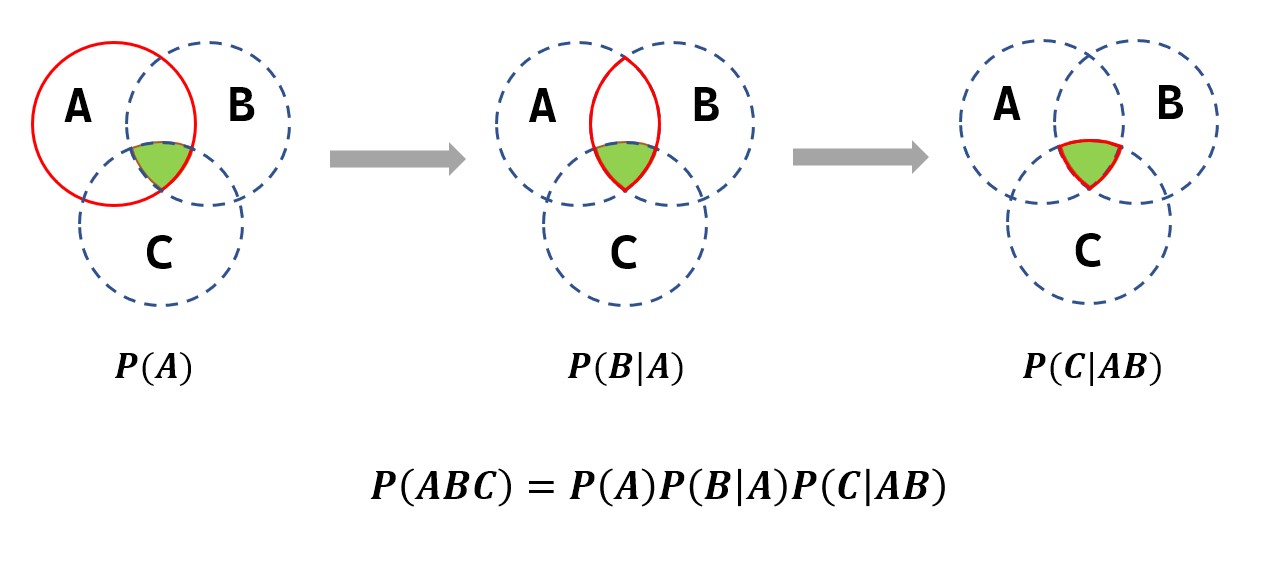
乘法公式可以推廣到任意有限個(gè)事件：

可以理解為逐步畫圈，縮小范圍直到精準(zhǔn)命中指定交集：（這里用\(n=3\)為例）

全概率公式

• \(\{A_i\}\)是\(E\)的完備事件組。
• \(P(A_i)>0\)。

則對(duì)于任意事件\(B\)，有：

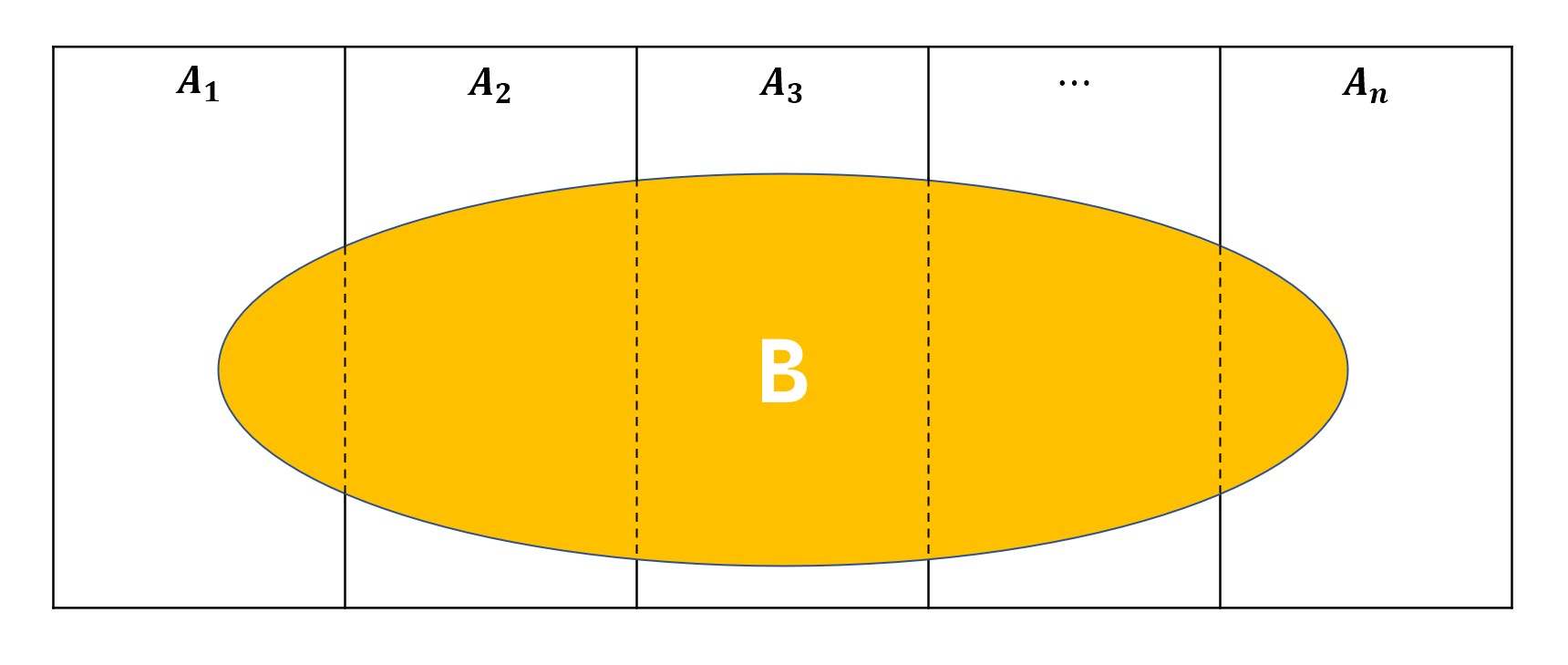
事實(shí)上，\(\{A_i\}\)不需要是\(E\)的完備事件集，只需要滿足\(\{A_i\}\)的并集能包住\(B\)即可。

貝葉斯公式

定義

• \(\{A_i\}\) 是完備事件組。
• \(P(A_i)>0\).

則對(duì)于任意事件\(B\)，\(P(B)>0\)，有：

• 分子部分：乘法公式
• 分母部分：全概率公式

相關(guān)概念

• \(P(A_i)\)稱為先驗(yàn)概率（在新信息到來(lái)之前）
• \(P(A_i|B)\)稱為后驗(yàn)概率（在新信息到來(lái)之后）

貝葉斯公式的特點(diǎn)是由果推因，\(A_i\)是原因，\(B\)是結(jié)果。在已知\(B\)已經(jīng)發(fā)生的情況下，推測(cè)“是\(A_i\)導(dǎo)致的”的可能性。

舉例：

事件\(B\)是“頭疼”，

事件\(\{A_i\}=\){

? "勞累過(guò)度",

? "普通感冒",

? "感染新冠",

? ......

}

解析：不管事件\(B\)是否發(fā)生，事件\(A_i\)都有各自發(fā)生的可能性，也就是先驗(yàn)概率\(P(A_i)\)。在事件\(B\)發(fā)生之后，后驗(yàn)概率\(P(A_i|B)\)表示“已經(jīng)頭疼了，是由事件\(A_i\)導(dǎo)致的概率是多少”。

注：在這個(gè)例子中：

• \(P(A_i|B)\)表示已經(jīng)頭疼了，是由事件\(A_i\)導(dǎo)致的可能性是多少。
• \(P(B|A_i)\)表示事件\(A_i\)已經(jīng)發(fā)生了（比如已經(jīng)感冒了），那么接下來(lái)會(huì)“頭疼”的可能性是多少。

二者不能搞混。

使用教材：
《概率論與數(shù)理統(tǒng)計(jì)》第四版 中國(guó)人民大學(xué) 龍永紅 主編 高等教育出版社