常用的統(tǒng)計分布，主要記錄了上側(cè)分位數(shù)、卡方分布、t分布和F分布的定義和性質(zhì)。

4.3 常用的統(tǒng)計分布

上側(cè)分位數(shù)

分位數(shù)是一個分界點。

上側(cè)分位數(shù)與分布函數(shù)\(F\)以及水平\(\alpha\)有關(guān)，常記為\(F_\alpha\).

含義：

在\(y=F(x)\)的圖像中，使得直線\(x=F_\alpha\)右側(cè)區(qū)域積分面積等于\(\alpha\)的\(F_\alpha\)就是上側(cè)分位數(shù)。

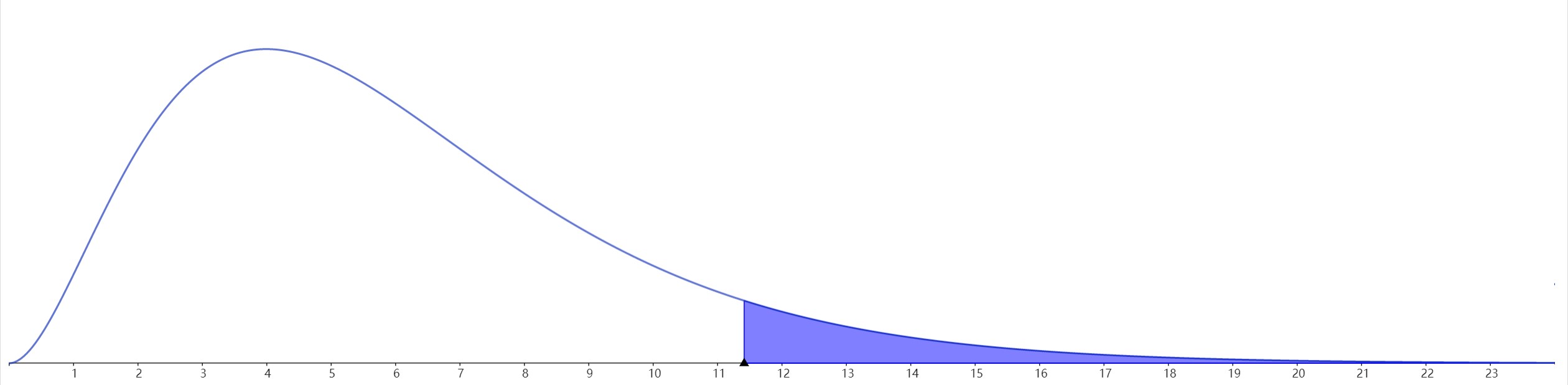
常見表述：\(P\{X>F_\alpha\}=\alpha\)

也就是找出使得右側(cè)面積等于\(\alpha\)的分界點\(F_\alpha\)，計算非常復(fù)雜，一般都是通過查表得到\(F_\alpha\).

---

\(\chi ^2\)分布

如果\(X_1,\cdots,X_n\)獨立，且\(X_i\sim N(0,1)\)，那么\(\sum\limits_{i=1}^nX_i^2\)服從\(\chi^2\)分布，記作\(\sum\limits_{i=1}^nX_i^2\sim \chi^2(n)\). 其中\(n\)稱為自由度。

• \(EX=n\)
• \(DX=2n\)

如果\(X\sim \chi^2(n)\)，當(dāng)\(n\)充分大時，\(\frac{X-n}{\sqrt{2n}}\)近似服從\(N(0,1)\)，即標(biāo)準(zhǔn)正態(tài)分布。

可加性

如果\(X\sim \chi^2(m),Y\sim\chi^2(n)\)，\(X,Y\)獨立，則\(X+Y\sim\chi^2(m+n)\).

推論

如果\(X_i\sim\chi^2(m_i)\)且獨立，其中\(1\le i\le n\)，則\(\sum\limits_{i=1}^nX_i\sim\chi^2(\sum\limits_{i=1}^nm_i)\).

---

t分布

\(X\sim t(n)\)

• 當(dāng)\(n\)很小，\(t\)分布與正態(tài)分布區(qū)別很大。
• 當(dāng)\(n\ge30\)時，\(t\)分布與正態(tài)分布的區(qū)別不大。

定義

如果\(X\sim N(0,1),Y\sim \chi^2(n)\)且\(X,Y\)獨立，則\(\frac{X}{\sqrt{Y/n}}\sim t(n)\).

\(t\)分布關(guān)于\(y\)軸對稱，因此其上側(cè)分位數(shù)有性質(zhì)：

---

F分布

\(X\sim F(n_1,n_2)\)

定義

如果\(X\sim \chi^2(n_1),Y\sim \chi^2(n_2)\)且\(X,Y\)獨立，則\(\frac{X/n_1}{Y/n_2}\sim F(n_1,n_2)\).

推論

如果\(X\sim F(n_1,n_2)\)，那么\(\frac{1}{X}\sim F(n_2,n_1)\).

上側(cè)分位數(shù)有性質(zhì)：

使用教材：
《概率論與數(shù)理統(tǒng)計》第四版 中國人民大學(xué) 龍永紅 主編 高等教育出版社