[概率論與數理統計]筆記：2.3 常用的離散型分布

這篇筆記介紹了常用的離散型分布，其中包含分布的定義、數學期望和方差的公式和參考圖像，最后包含了泊松定理的證明。

2.3 常用的離散型分布

退化分布

若隨機變量$X$滿足

\[P\{X=a\}=1 \]

則稱$X$服從$a$處的退化分布，這種情況下，隨機變量退化成了一個確定的常數。

兩點分布

定義

若隨機變量$X$只有兩個可能取值，設其分布為

\[P\{X=x_1\}=p,\quad P\{X=x_2\}=1-p,\quad 0<p<1, \]

則稱$X$服從$x_1,x_2$處參數為$p$的兩點分布。

如果$x_1=1,x_2=0$，則稱為0-1分布或伯努利分布，也稱$X$為伯努利隨機變量。

性質

當$x_1=1,x_2=0$時，有$EX=p,\quad DX=p(1-p)=pq$，其中$q=1-p$.

兩點分布也可以表示為：$P\{X=k\}=p^k(1-p)^{1-k},\quad k=0,1$

兩點分布是二項分布的特例

聯系

伯努利試驗

圖像

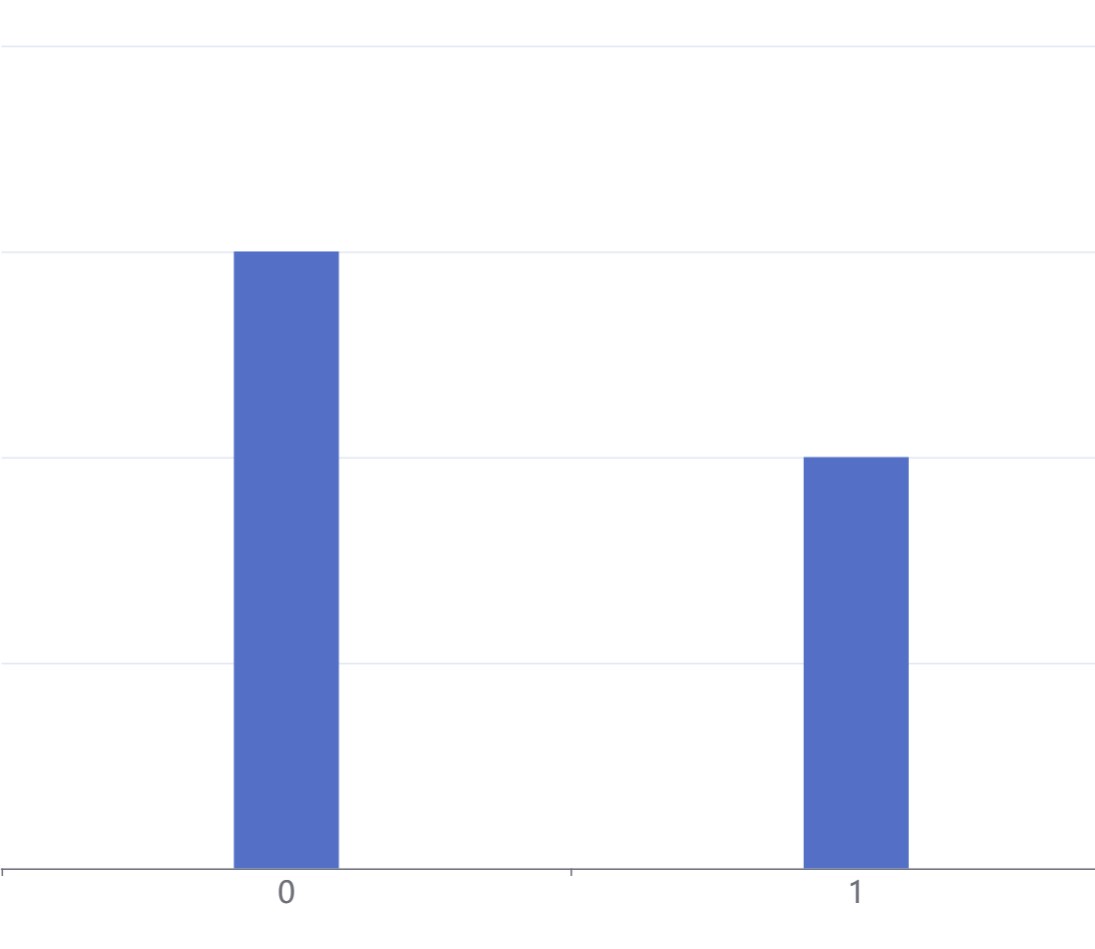
n個點上的均勻分布

定義

如果隨機變量$X$的分布滿足

\[P\{X=x_i\}=\frac{1}{n},\quad i=1,2,\cdots,n, \]

則稱$X$服從$n$個點$\{x_1,x_2,\cdots,x_n\}$上的均勻分布。

性質

$EX=\frac{1}{n}\sum\limits_{i=1}^nx_i=\overline{x}$

$DX=\frac{1}{n}\sum\limits_{n-1}^n(x_i-\overline{x})^2$

數學期望的本質是加權平均數，權重就是對應的概率，在均勻分布中，每個權重都是相等的，所以數學期望就等于算術平均數。

聯系

古典概型

圖像

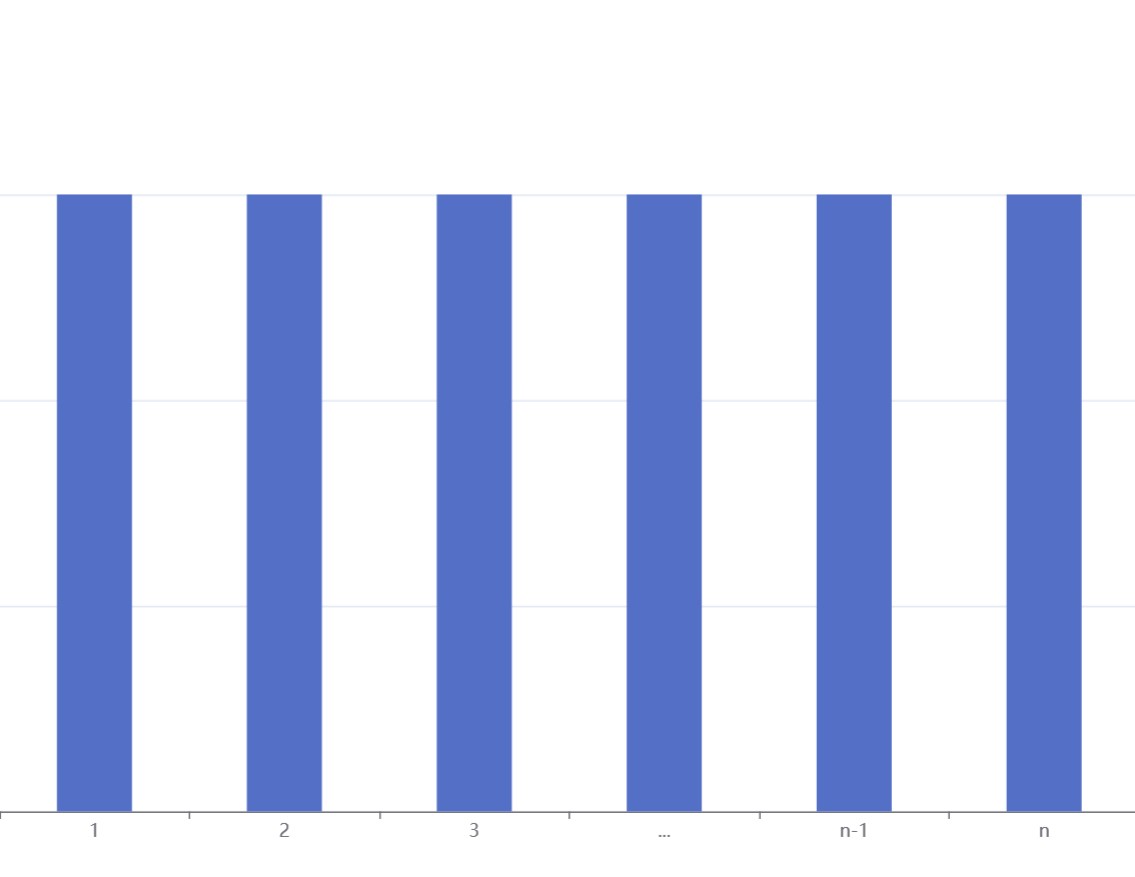
二項分布

定義

事件$A$發生的概率為$p$，$n$次試驗，發生了$k$次。

如果$X$的分布滿足

\[P\{X=k\}=C_n^kp^k(1-p)^{n-k},\quad k=0,1,2,\cdots,n, \]

則稱$X$服從參數為$n,p$的二項分布，并記作$X\sim B(n,p)$.

記$B(k;n,p)=C_n^kp^k(1-p)^{n-k}$.

當$n=1$時，二項分布$B(1,p)$就是參數為$p$的0-1分布。

性質

最可能值
- 若$(n+1)p$不為整數，則$[(n+1)p]$達最大值，其中$f(x)=[x]$是取整函數。
- 若$(n+1)p$為正數，則$(n+1)p,\ \ (n+1)p-1 $是最大值。
數學期望：$EX=np$
方差：$DX=npq$

聯系

$n$重伯努利試驗

圖像

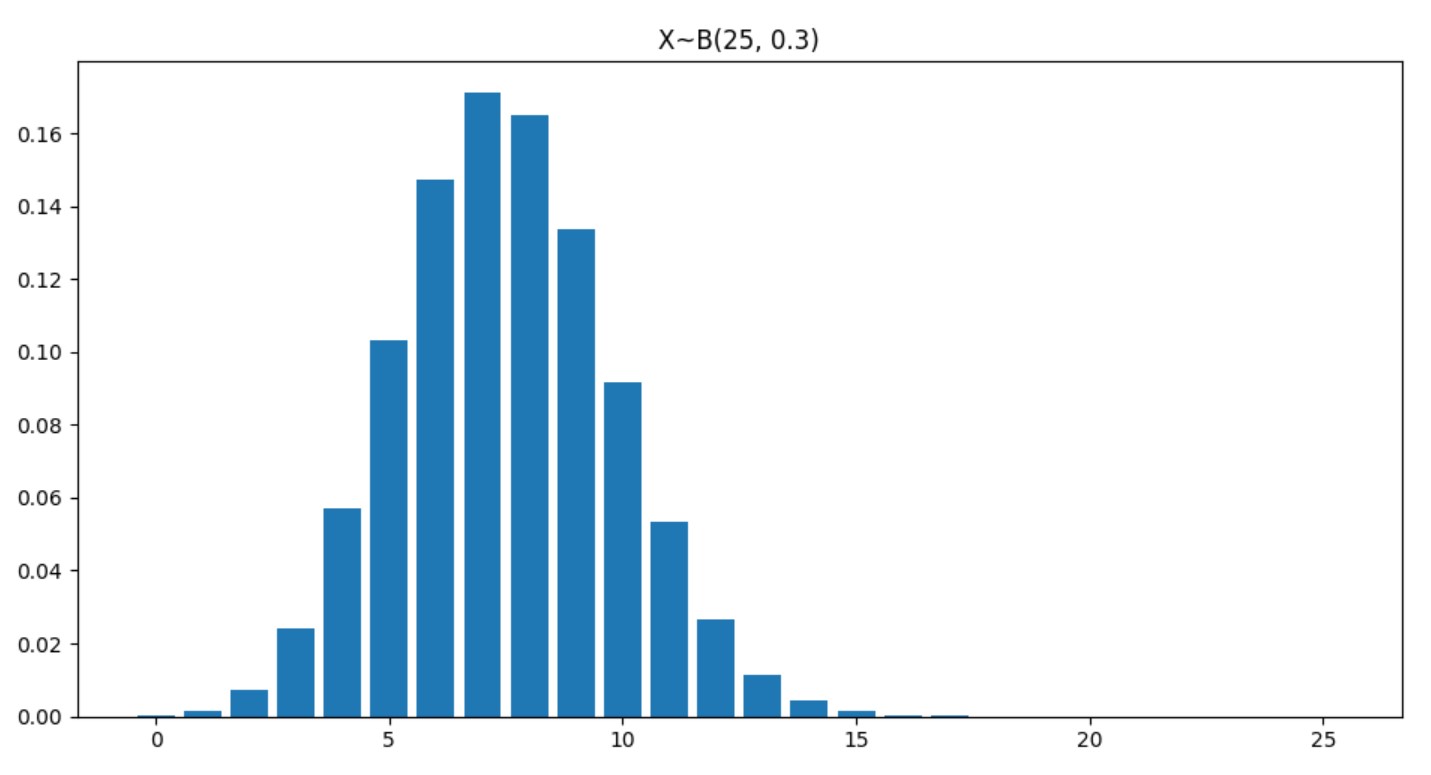
幾何分布

定義

$P(A)=p$，第$k$次首次發生，前$k-1$次不發生的概率為

\[P\{X=k\}=(1-p)^{k-1}p=q^{k-1}p,\quad k\ge1 \]

這樣的分布就叫幾何分布，記為$X\sim G(p)$.

之所以稱為“幾何”是因為$q^{k-1}p$是一個幾何數列（也叫等比數列）。

性質

數學期望：$EX=\frac{1}{p}$
方差：$DX=\frac{q}{p^2}$
無記憶性：$P\{X>m+n|X>m\}=P\{X>n\}$

對于無記憶性的理解：就算之前做過了$m$次試驗，對于接下來的$n$次試驗是沒有影響的。

計算

$P\{X=k\}=q^{k-1}p$
$P\{X>m\}=\sum\limits_{k=m+1}^\infty q^{k-1}p$

圖像

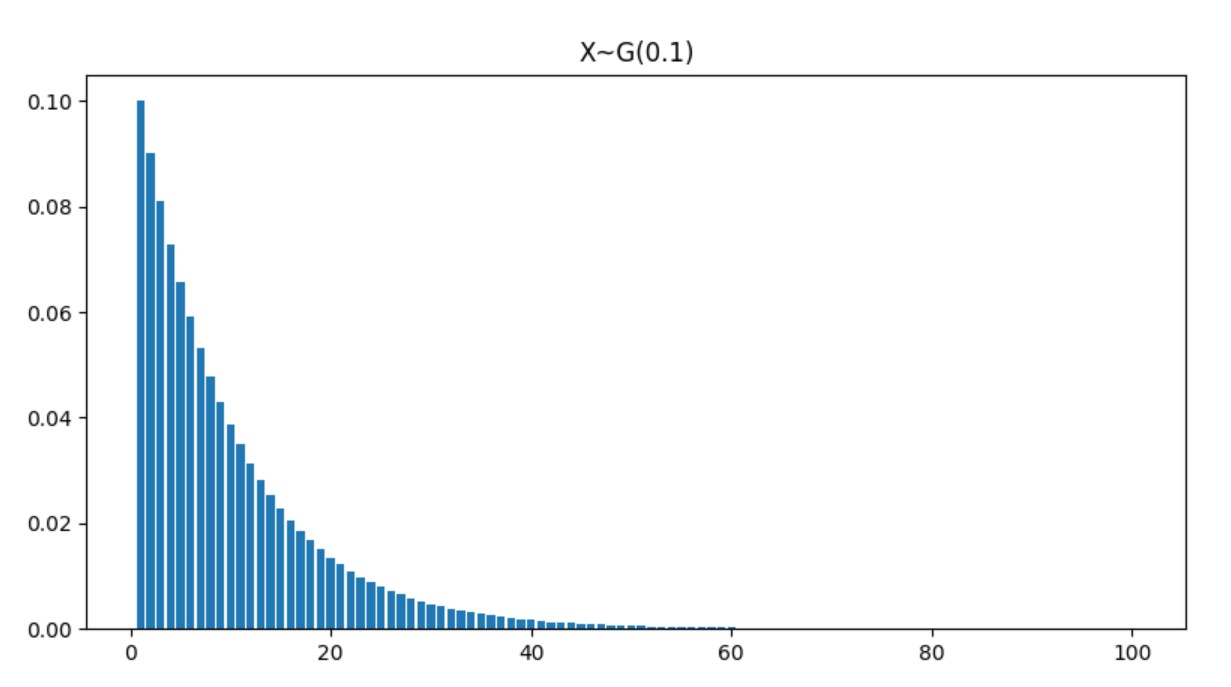
超幾何分布

定義

$N$個元素分為兩類，個數分別為$N_1,N_2$，即$N=N_1+N_2$。從$N$個元素中取出$n$個元素，設隨機變量$X$為$n$個元素中屬于第一類元素的個數，則

\[P\{X=k\}=\frac{C_{N_1}^kC_{N_2}^{n-k}}{C_N^n},\quad k=0,1,2,\cdots.min\{n,N_1\} \]

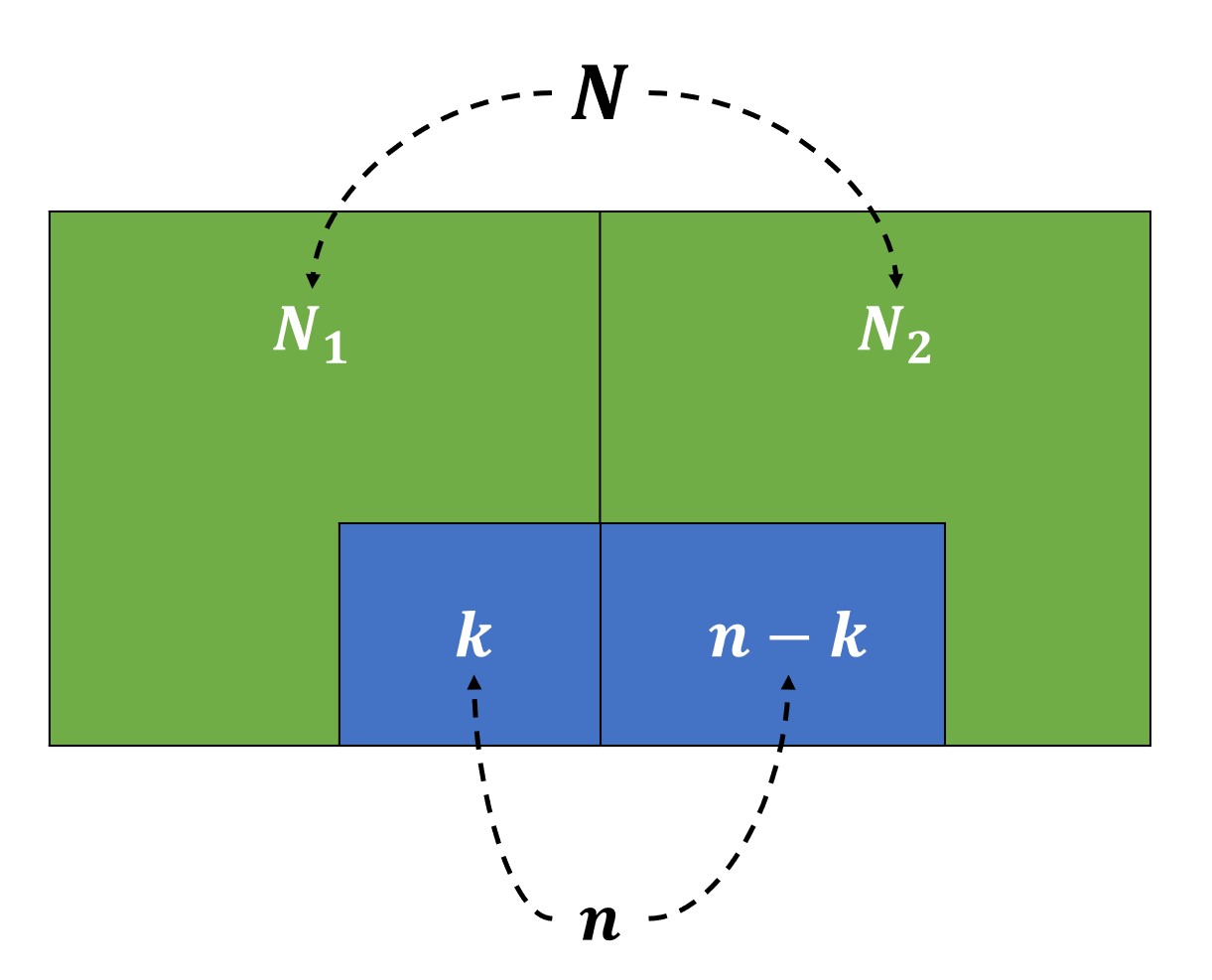
該分布稱為超幾何分布，記作$X\sim H(N,n,N_1)$，（也有$X\sim H(N,N_1,n)$的記法）。

有時候會把$N_1,N_2$記作$M,N-M$.

$X\sim H(N,n,M)$或$X\sim H(N,M,n)$

聯系

超幾何分布是不放回的抽取，二項分布是放回的抽取。
當$N,N_1,N_2$很大時，可以用二項分布作為超幾何分布的近似：

當$N\to\infty,N_1\to\infty,N_2\to\infty$，且$\frac{N_1}{N}\to p,\ \frac{N_2}{N}\to q$，對于任意給定的$n$和$k$，有

\[\lim\limits_{N\to\infty}\frac{C_{N_1}^kC_{N_2}^{n-k}}{C_N^n}=C_n^kp^kq^{n-k} \]

理解：當$N_1$和$N_2$都很大時，從中拿走一個不放回，數量幾乎不變，相當于放回。

性質

數學期望：$EX=n\cdot\frac{N_1}{N}$
方差：$DX=n\cdot\frac{N_1}{N}\cdot\frac{N_2}{N}\cdot\frac{N-n}{N_1}$

圖像

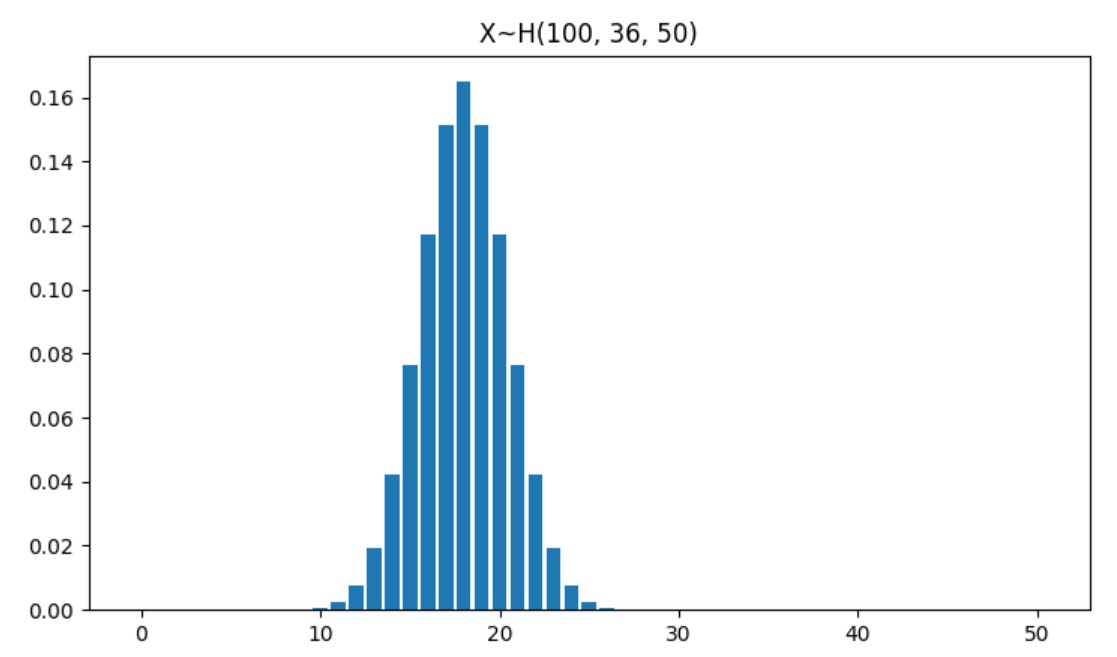
這里的參數分別是$N=100,\ M=36,\ n=50.$

泊松分布

定義

如果一個隨機變量$X$的概率分布為

\[P\{x=K\}=\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0,1,2,\cdots \]

其中$\lambda>0$為參數，則稱$X$服從參數為$\lambda$的泊松分布，記作$X\sim P(\lambda)$.

這里的記號$P$是指Poisson。

聯系

泊松分布可以用于近似表示二項分布，這是因為當二項分布的$n\to\infty,\ p\to0,\ np=\lambda$時，二項分布就成為了泊松分布。

泊松定理：在$n$重伯努利試驗中，事件$A$在每次試驗中發生的概率為$p_n$(這里的概率與試驗總數$n$有關)，如果$n\to\infty$時，$np\to\lambda$（$\lambda>0$為常數），則對任意給定的$k$，有

\[\lim\limits_{n\to\infty}B(k;n,p)=\lim\limits_{n\to\infty}C_n^kp^k(1-p)^{n-k}=\frac{\lambda^k}{k!}e^{-\lambda} \]

證明過程如下：

前提條件有：$n\to\infty,\ p\to0,\ np=\lambda$，所以有$p=\frac{\lambda}{n}$.

需要用到的公式：$C_n^k=\frac{n!}{k!(n-k)!}$，$\lim\limits_{x\to\infty}(1+\frac{1}{x})^x=e$.

首先，將$p=\frac{\lambda}{n}$和組合數公式代入，則

\[\lim\limits_{n\to\infty}C_n^kp^k(1-p)^{n-k}=\lim\limits_{n\to\infty}\frac{n!}{k!(n-k)!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k} \]

將$n!$和$(n-k)!$進行化簡：

\[\frac{n!}{k!(n-k)!}=\frac{n(n-1)\cdots(n-k+1)}{k!} \]

因此，

\[原式=\lim\limits_{n\to\infty}\frac{n(n-1)\cdots(n-k+1)}{k!}\frac{\lambda^k}{n^k}(1-\frac{\lambda}{n})^{n-k} \]

此時關注分子的$n(n-1)\cdots(n-k+1)$，以及分母的$n^k$（兩者都是有$k$項相乘）：

\[\begin{align*} \lim\limits_{n\to\infty}\frac{n(n-1)\cdots(n-k+1)}{n^k} &=\lim\limits_{n\to\infty}\frac{n}{n}\cdot\frac{n-1}{n}\cdots\frac{n-k+1}{n} \\ &=\lim\limits_{n\to\infty}1\times(1-\frac{1}{n})\times\cdots\times(1-\frac{k-1}{n}) \\ &=\lim\limits_{n\to\infty}1\times1\times\cdots\times1 \\ &=1 \end{align*} \]

因此，

\[原式=\lim\limits_{n\to\infty}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k} \]

此時，再關注$\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k}$，

\[\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k} = \lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n(1-\frac{\lambda}{n})^{-k} \]

其中，因為$n\to\infty$，且$\lambda,\ k$都是有限值，所以$(1-\frac{\lambda}{n})\to1$，所以$\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{-k}=1$

所以$\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k}=\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n$

又因為

\[\begin{align*} \lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n &= \lim\limits_{n\to\infty}(1+\frac{1}{-\frac{n}{\lambda}})^n\quad\quad //\ \lambda從分子移到分母 \\ &= \lim\limits_{n\to\infty}[(1+\frac{1}{-\frac{n}{\lambda}})^{-\frac{n}{\lambda}}]^{-\lambda}\quad\quad //\ 指數拼湊出與自然對數重要極限一致的形式\\ &= e^{-\lambda} \end{align*} \]

因此

\[\begin{align*} 原式 &= \lim\limits_{n\to\infty}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k}\\ &= \frac{\lambda^k}{k!}\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k}\quad\quad//\ 常數提取 \\ &= \frac{\lambda^k}{k!}\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n\quad\quad//\ 根據上面的推導 \\ &= \frac{\lambda^k}{k!}e^{-\lambda} \end{align*} \]

證明完畢，

\[\lim\limits_{n\to\infty}C_n^kp^k(1-p)^{n-k}=\frac{\lambda^k}{k!}e^{-\lambda} \]

證明思路和下面的案例分析來源于B站視頻??泊松分布是怎么來的？應該怎么用？

性質

數學期望：$EX=\lambda$
方差：$DX=\lambda$

案例分析

假設有一停車場，1min進入了3輛車，目標是預測1min進入5輛車的概率。

將1min進行$n$等分，且$n\to\infty$，表示1min做了$n$次伯努利試驗。

將$\frac{1}{n}$時間內進入一輛車的概率記為$p$，則$p\to0$。

此時，$\lambda=np=3$.

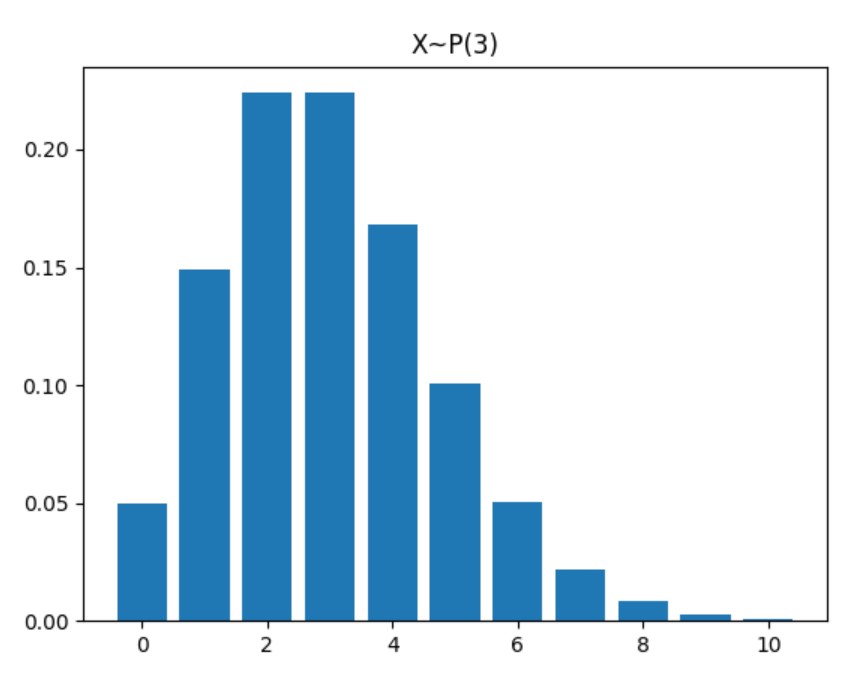
對應的泊松分布為：$P\{X=k\}=\frac{3^k}{k!}e^{-3}$

所以1min進入5輛車的概率為：$P\{X=5\}=\frac{3^5}{5!}e^{-3}\approx0.10081881$

圖像

使用教材：
《概率論與數理統計》第四版中國人民大學龍永紅主編高等教育出版社

posted @ 2023-01-06 19:06 feixianxing 閱讀(848) 評論(0) 收藏舉報

刷新頁面返回頂部

feixianxing