2.4 常用的連續型分布

均勻分布

定義

如果隨機變量\(X\)的密度函數為

則稱\(X\)服從\([a,b]\)上的均勻分布，記作\(X\sim U[a,b]\).

性質

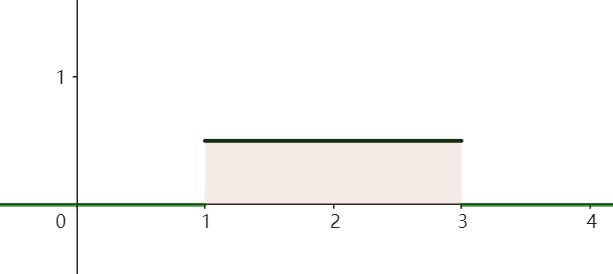
• \(\int_{-\infty}^{+\infty}f(x)dx=\int_a^bf(x)dx=1\)

矩形面積為1，因此區間\([a,b]\)上的常數必定為\(\frac{1}{b-a}\).

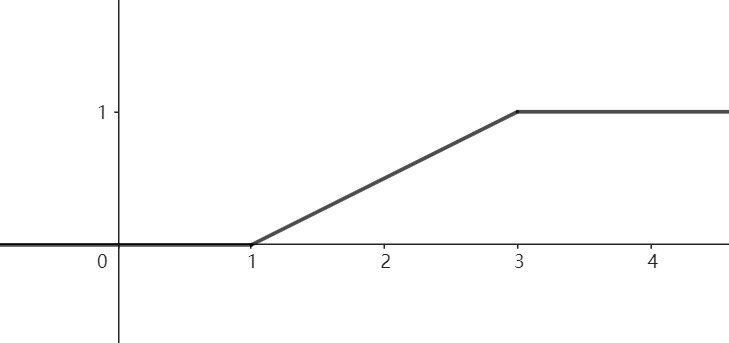
• 分布函數：

當\(a\le x\le b\)時，

• 若\([c,d]\)是\([a,b]\)子區間，則\(P\{c\le X\le d\}=\int_c^d\frac{1}{b-a}dt=\frac{d-c}{b-a}\)。即概率與區間長度成正比。

• 數學期望：\(EX=\frac{a+b}{2}\)

證明：

• 方差：\(DX=\frac{(b-a)^2}{12}\)

簡略地證明：

相關知識點：

1. \(DX=EX^2-(EX)^2\)
2. 隨機變量函數的數學期望(連續型)：\(\int_{-\infty}^{+\infty}g(x)f(x)dx\)
3. \(b^3-a^3=(b-a)(b^2+ab+a^2)\)

聯系

幾何概型

指數分布

定義

如果隨機變量\(X\)的密度函數為

其中\(\lambda>0\)為參數，則稱\(X\)服從參數為\(\lambda\)的指數分布，記作\(X\sim e(\lambda)\).

分布函數

數學期望

方差

性質

• 無記憶性：\(P\{X>r+s|X>s\}=P\{X>r\}\)

聯系

• 指數分布與泊松分布之間的聯系：

  如果用參數為\(\lambda\)的泊松分布描述單位時間事件發生的次數，那么一次事件發生的等待時間便服從參數為\(\lambda\)的指數分布。

• 指數分布與幾何分布之間的聯系：

  • 指數分布描述事件發生等待的時間（連續量）
  • 幾何分布描述事件發生等待的次數（離散量）

正態分布

定義

如果隨機變量\(X\)的密度函數為

其中\(\mu,\sigma\)為常數，且\(\sigma>0\)，則稱\(X\)服從參數為\(\mu\)和\(\sigma^2\)的正態分布，記作\(X\sim N(\mu,\sigma^2)\).

分布函數

由于密度函數的原函數沒有解析表達式，因而其分布函數（記作\(\varPhi(x)\)）不能表示為解析式。

性質

• \(\int_{-\infty}^{+\infty}\varphi(x)dx=1\).

證明：

前置知識點：根據歐拉-泊松積分，有\(\int_{-\infty}^{+\infty}e^{-x^2}dx=\sqrt{\pi}\) ??泊松積分的兩種計算方法

正態分布的密度函數的系數之所以這么復雜就是為了使其積分等于1.

• \(EX=\mu\)

• \(DX=\sigma^2\)

• \(\varphi(x)\)關于\(x=\mu\)對稱，并在\(x=\mu\)處取得最大值\(\frac{1}{\sqrt{2\pi}\sigma}\)

理解：密度函數的\(x\)位于右上角指數部分的\((x-\mu)^2\)，結合偶函數的性質，不難得出該函數圖像關于\(x-\mu\)對稱。

• \(y=\varphi(x)\)以\(x\)軸為漸近線。
• \(x=\mu\pm\sigma\)為拐點。
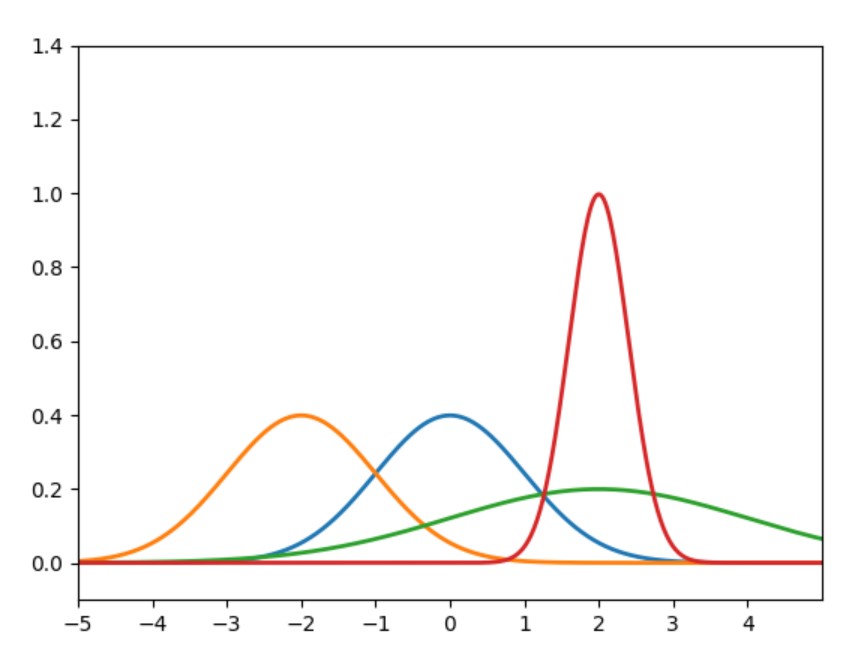
• \(\sigma\)不變，\(\mu\)改變，圖像左右平移。
• \(\mu\)不變，\(\sigma\)改變，圖像對稱軸固定：
  • \(\sigma\)變大，最高點下降，圖像矮胖，變緩。
  • \(\sigma\)變小，最高點上升，圖像高瘦，變陡。

標準正態分布

定義

當\(\mu=0,\sigma^2=1\)時，即\(X\sim N(0,1)\)，稱\(X\)服從標準正態分布，其密度函數記作\(\varphi_0(x)\)，即

分布函數：

通常計算概率的方法是：

1. 將一般正態分布變換為標準正態分布。
2. 查詢標準正態分布表的概率值。

性質

• 密度函數圖像關于\(y\)軸對稱，是偶函數：\(\varphi_0(x)=\varphi_0(-x)\)。對于分布函數，有\(\varPhi_0(-x)=1-\varPhi_0(x)\).

一般正態分布與標準正態分布

• 設\(X\sim N(\mu,\sigma^2),Y=aX+b\)，\(a,b\)為常數，且\(a\ne 0\)，則\(Y\sim N(a\mu+b, a^2\sigma^2)\).

• 如果\(X\sim N(\mu,\sigma^2)\)，則\(Z=\frac{X-\mu}{\sigma}\sim N(0,1)\).

這里的\(Z\)稱為\(X\)的標準化。

• \(X\sim N(\mu,\sigma^2)\)的充要條件是存在一個隨機變量\(Z\sim N(0,1)\)，使得\(X=\sigma Z+\mu\).

• 設\(X\sim N(\mu,\sigma^2),\varPhi(x),\varphi(x)\)分別為其分布函數與密度函數，\(\varPhi_0(x),\varphi_0(x)\)是標準正態分布的分布函數和密度函數，則有

這里給出第二個式子的證明過程：

已知

則

證明完畢。

使用教材：
《概率論與數理統計》第四版 中國人民大學 龍永紅 主編 高等教育出版社