如何用隨機方法求解組合優化問題（五）
模擬退火算法
這是一篇筆記，是對于B站up主馬少平的視頻（第四篇 如何用隨機方法求解組合優化問題（五））的學習與記錄。
前置知識回顧
【回顧】：局部最優問題
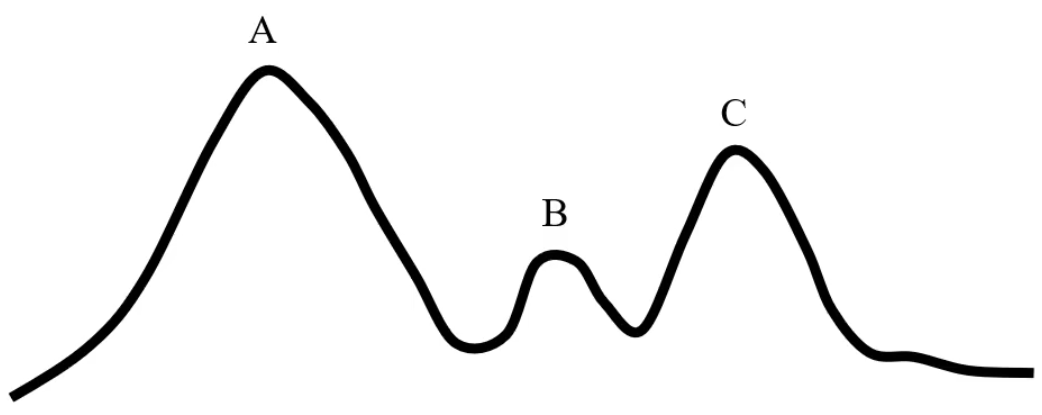
在局部搜索問題中，可能會陷入局部最優解（如上圖中的B、C），解決思路是：以概率接受差解。
【回顧】：退火過程中
從狀態 \(i\) 轉換為狀態 \(j\) 的轉換準則：
-
如果 \(E(j)\le E(i)\)，則狀態轉換被接受；
-
如果 \(E(j)>E(i)\)，則狀態轉移被接受的概率為：
\[e^{\frac{E(i)-E(j)}{KT}} \]
根據上述特點，可以發現局部搜索和退火過程存在一定關聯，可以嘗試將局部搜索與退火過程結合用于求解組合優化問題。
組合優化問題與退火過程的類比
算法設計
基本思想
在局部搜索算法中，從領域中隨機選擇一個解 \(j\) ，如果該解的指標函數好于當前解 \(i\) 的指標函數，則以概率1接受該解，否則按照以下概率接受該解：
\[e^{\frac{f(i)-f(j)}{t}}
\]
這里假定求解最小解，其中 \(f(i)\) 為解 \(i\) 的指標函數，\(t\) 為控制參數，也稱作溫度。
偽代碼
- 隨機選擇一個解 \(i\)，\(k=0\)，\(t_0=T_{\max}\)（初始溫度），計算指標函數 \(f(i)\).
- \(t=t_k\)，如果滿足結束條件，則轉（15）.
- Begin
- ??如果在該溫度內達到了平衡條件，則轉（13）.
- ??Begin
- ????從 \(i\) 的領域 \(N(i)\) 中隨機選擇一個解 \(j\) .
- ????計算指標函數 \(f(j)\).
- ????如果 \(f(j)\le f(i)\)，則接受 \(j\)，\(i=j\)，\(f(i)=f(j)\)，轉（4）.
- ????否則計算 \(P_{i\Rightarrow j}(t)=e^{-\frac{f(j)-f(i)}{t}}\)
- ??????如果 \(Random(0, 1)<P_{i\Rightarrow j}(t)\)，則接受 \(j\)，\(i=j\)，\(f(i)=f(j)\).
- ????轉（4）.
- ??End
- ??對 \(t\) 降溫，\(t_{k+1}=Drop(t_k)\)，\(k=k+1\)，轉（2）.
- End
- 輸出結果.
- 結束.
分析：
- 首先隨機選擇一個解，比如旅行商問題中，先隨機生成一條路線。
- 初始溫度需要設置一個較大的數，這是因為“接受較差的解”的概率與溫度有關，初始溫度設置較大在某種程度上可以幫助跳出局部最優解，而提高了找到全局最優解的可能性。
- 指標函數用于衡量解的優良性，比如在旅行商問題中是“路線長度”。
- 算法包含內外兩層循環：
- 內循環為“保持溫度不變，在鄰域內按照退火的特點，嘗試找到可以接受的解”。如果是好解則直接接受，如果是差解則按概率接受。
- 外循環負責“降溫”，每次降溫后，如果還沒達到平衡條件，則繼續尋找解。
以上只是算法的簡單框架，還有一些問題需要解決。
算法需要解決的問題：
- 初始溫度 \(t_0\)
- 溫度 \(t\) 的衰減函數
- 算法的終止標準
- 每個溫度 \(t\) 下的馬爾可夫鏈長度 \(L_k\)
只有這些參數確定之后，算法才算完整，才能用于解決實際問題。
算法性質
與退火過程一樣，當滿足條件時：
- 初始溫度足夠高
- 在每個溫度下狀態的交換足夠充分
- 溫度 \(t\) 的下降足夠緩慢
模擬退火算法以概率1收斂到最優解。
浙公網安備 33010602011771號