如何用隨機方法求解組合優化問題（四）

退火是固體物理學中的一個概念，它描述了固體材料在高溫下逐漸冷卻的過程，以使其從高能態逐漸轉變為低能態。這個概念在模擬退火算法中得到了應用，用于尋找問題的最優解。這篇筆記還沒有介紹到模擬退火算法，而是記錄退火這一物理過程以及相關的公式。最主要的內容是如何將退火過程的特點遷移到后續的算法設計中。

模擬退火算法中的退火過程是什么

這是一篇筆記，是對于B站up主馬少平的視頻（第四篇如何用隨機方法求解組合優化問題（四））的學習與記錄。

這篇筆記還沒有介紹到模擬退火算法，而是記錄退火這一物理過程以及相關的公式。

最主要的內容是如何將退火過程的特點遷移到后續的算法設計中。

退火是什么

退火是固體物理學中的一個概念，它描述了固體材料在高溫下逐漸冷卻的過程，以使其從高能態逐漸轉變為低能態。這個概念在模擬退火算法中得到了應用，用于尋找問題的最優解。

退火有以下過程：

加熱階段（高溫階段）：在退火過程開始時，固體物體會被加熱到非常高的溫度。高溫會使原子或分子的熱運動劇烈，突破原本的位置限制。這種高溫狀態下，固體處于高能態，原子或分子的位置非常不穩定。
冷卻階段（退火階段）：隨著時間的推移，溫度逐漸降低。在溫度逐漸降低的過程中，原子或分子的熱運動減緩，逐漸趨向于更穩定的位置。隨著溫度的降低，固體會逐漸從高能態轉變為低能態，原子或分子逐漸排列成更有序的結構。
冷卻到基底溫度（低溫階段）：當溫度足夠低時，固體達到了最低能態，原子或分子的運動幾乎停止，形成了穩定的結晶態。此時，固體的內部結構和排列達到了最優狀態，對應著系統的全局最優解。

在模擬退火算法中，這個物理過程被用來模擬在解空間中尋找最優解的過程。算法從一個初始解（高溫狀態）開始，隨機生成新的解（狀態），并根據一定的準則決定是否接受新解。隨著算法的迭代，模擬退火算法會逐漸減小“溫度”，也就是接受劣解的概率，從而使算法在解空間中逐漸趨向于全局最優解，就像實際的退火過程一樣。

退火過程

在退火過程中，狀態轉換的標準為：

如果 \(\Delta E \le 0\) ，則新狀態被接受；
如果 \(\Delta E > 0\) ，則新狀態被接受的概率為：

\[P = e^{-\frac{\Delta E}{KT}} \]

其中 \(\Delta E\) 是新狀態的內能和初始狀態的內能的差值，\(T\) 是絕對溫度，\(K>0\) 是玻爾茲曼常數。

在給定的溫度 \(T\) 下，當進行足夠多次的狀態轉換后，系統將達到一種熱平穩狀態。

此時系統處于某個狀態 \(i\) 的概率 \(P_i(T)\) 由 Boltzmann 分布給出：

\[P_i(T)=\frac{e^{-\frac{E(i)}{KT}}}{Z_T} \]

其中 \(Z_T=\sum\limits_{j\in S}e^{-\frac{E(j)}{KT}}\) 為歸一化因子。

退火過程分析

同一溫度下兩個內能不同的狀態

假設兩個狀態的內能 \(E(i)<E(j)\)：

\[\begin{align*} P_i(T)-P_j(T) &= \frac{e^{-\frac{E(i)}{KT}}}{Z_T} - \frac{e^{-\frac{E(j)}{KT}}}{Z_T} \\ &= \frac{1}{Z_T}e^{-\frac{E(i)}{KT}} \left( 1-\frac{e^{-\frac{E(j)}{KT}}}{e^{-\frac{E(i)}{KT}}} \right ) \\ &= \frac{1}{Z_T}e^{-\frac{E(i)}{KT}} \left ( 1-e^{-\frac{E(j)-E(i)}{KT}} \right ) \end{align*} \]
因為 \(E(i)<E(j)\)，可以推出\(0<e^{-\frac{E(j)-E(i)}{KT}}<1\)，于是有 \(P_i(T)-P_j(T) >0\)，即 \(P_i(T)>P_j(T)\)

結論：在任何溫度 \(T\) 下，系統處于低內能的狀態的概率大于處于高內能的狀態的概率。

高溫下的情況

\[\begin{align*} \lim_{T\to \infty}P_i(T) &= \lim_{T\to \infty} \left[ \frac{e^{-\frac{E(i)}{KT}}}{\sum\limits_{j\in S}e^{-\frac{E(j)}{KT}}} \right ] \\ &= \frac{1}{|S|} \end{align*} \]

? 其中 \(|S|\) 表示系統所有可能的狀態數。

? 結論：當溫度趨近于無窮大時，系統處于各個狀態的概率相等，處于均勻分布，與所處狀態的內能無關。

低溫下的情況

\[\begin{align*} \lim_{T\to 0}P_i(T) &= \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)}{KT}}}{\sum\limits_{j\in S}e^{-\frac{E(j)}{KT}}} \right] = \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)-E_m}{KT}}}{\sum\limits_{j\in S}e^{-\frac{E(j)-E_m}{KT}}} \right] \\ &= \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)-E_m}{KT}}}{\sum\limits_{j\in S_m}e^{-\frac{E(j)-E_m}{KT}}+\sum\limits_{j\notin S_m}e^{-\frac{E(j)-E_m}{KT}}} \right] = \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)-E_m}{KT}}}{\sum\limits_{j\in S_m}e^{-\frac{E(j)-E_m}{KT}}} \right] \\ &= \begin{cases} \frac{1}{|S_m|}, & if \quad i\in S_m \\ 0, & if \quad i \notin S_m \end{cases} \end{align*} \]

? 其中 \(S_m\) 表示系統最小內能狀態的集合，\(E_m\) 表示系統的最小內能。

? 結論：當溫度趨近于絕對0度時，系統以等概率趨近于幾個內能最小的狀態之一，而系統處于其它狀態的概率為0。即系統達到內能最小狀態的概率為1。

溫度緩慢下降時的情況

\[\begin{align*} \frac{\partial P_i(T)}{\partial T} &= \frac{\partial}{\partial T} \left[ \frac{e^{-\frac{E(i)}{KT}}}{Z_T} \right] \\ &= \frac{P_i(T)}{KT^2}[E(i)-\overline{E_T}] \begin{cases} >0 \quad if \ E(i)>\overline{E_T}, \quad 高能狀態 \\ <0 \quad if \ E(i)<\overline{E_T}, \quad 低能狀態 \end{cases} \end{align*} \]

? 其中 \(\overline{E_T}=\sum\limits_{j\in S}E(j)P_j(T)\) 為狀態內能的平均值。

? 結論：系統處于低能狀態的概率隨著溫度的下降單調上升，而系統處于高能狀態的概率隨著溫度的下降單調下降。

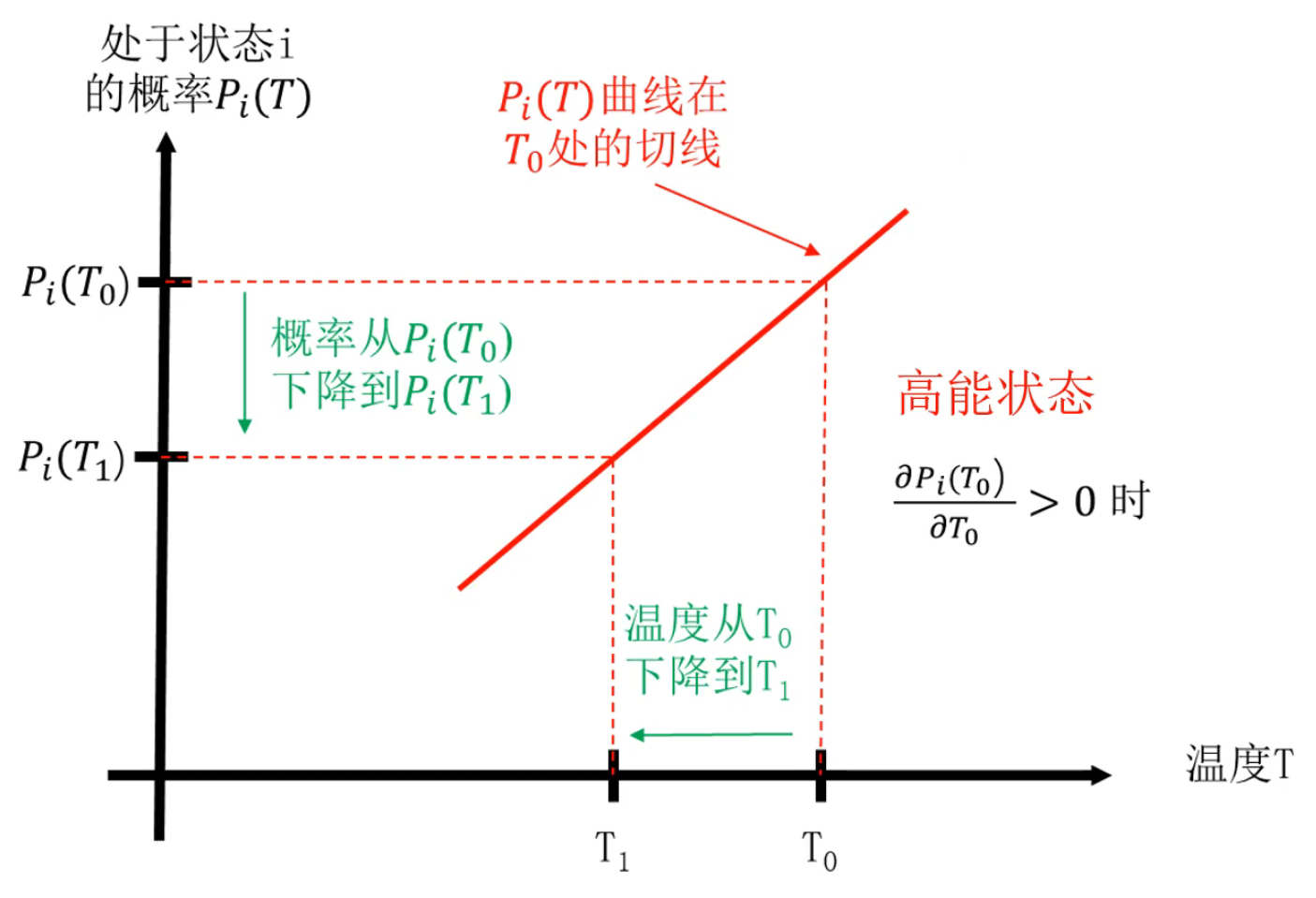
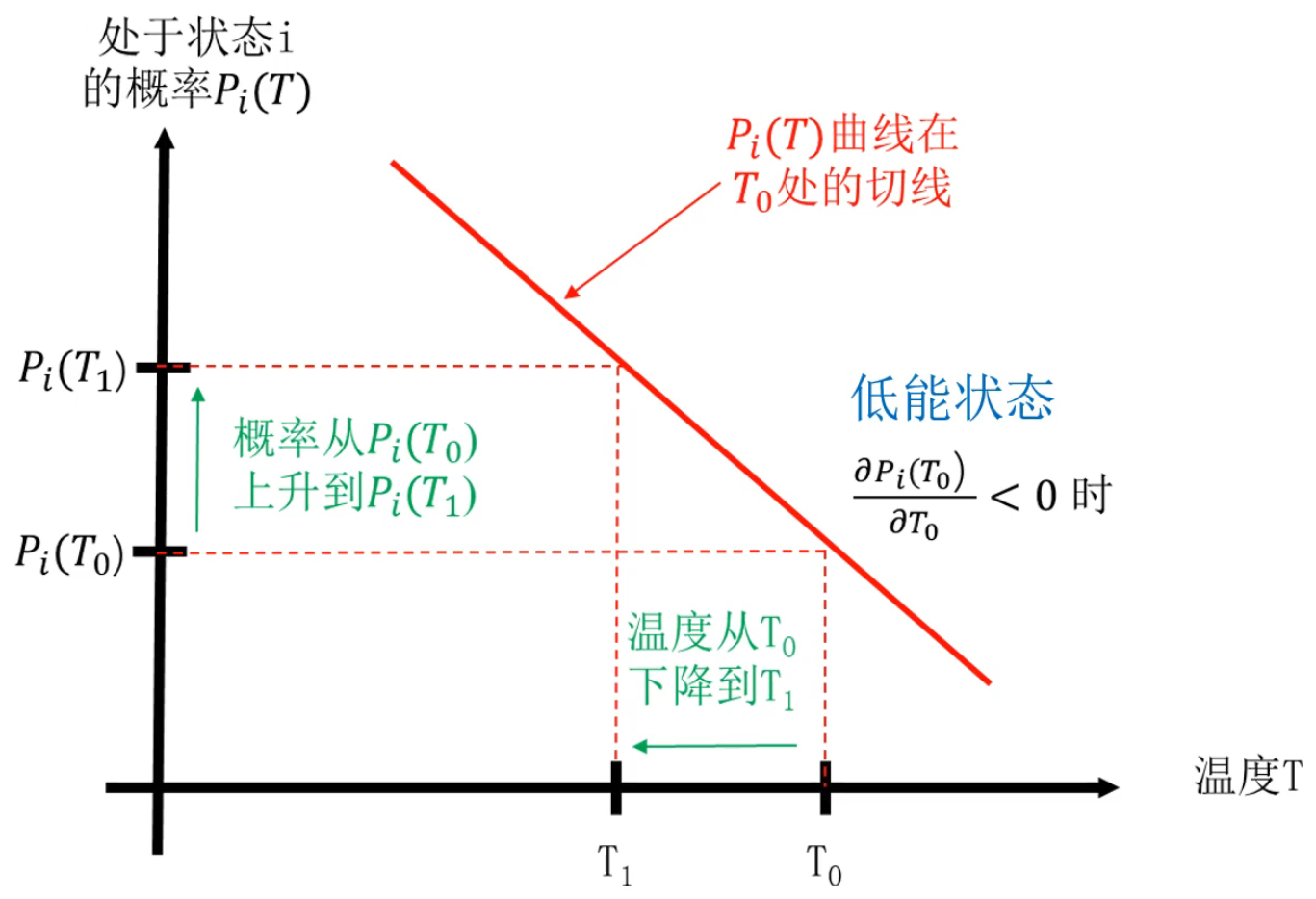
分析：

隨著溫度的緩慢下降，由于處于低能狀態的概率越來越大，處于高能狀態的概率越來越小，導致狀態的內能平均值 \(\overline{E_T}\) 隨溫度下降而下降，從而使得更多的狀態屬于高能狀態，越來越少的狀態屬于低能狀態。最終，當溫度降低到趨近于絕對0度時，只有具有最小內能的狀態才屬于低能狀態。
這也從另一個角度說明了當溫度趨近于絕對0度時，為什么系統處于最小內能狀態的概率為1，這與我們前面的分析是一致的。

退火過程總結

在溫度不變時，處于低內能狀態的概率大于處于高內能狀態的概率；
當溫度趨于無窮大時，系統等概率處于各個狀態；
當溫度趨于絕對0度時，系統達到內能最小狀態的概率為1；
當溫度緩慢下降時，系統處于低能狀態的概率隨著溫度的下降單調上升，而系統處于高能狀態的概率隨著溫度的下降單調下降。
退火過程的三個條件：
- 初始溫度必須足夠高；
- 在每個溫度下狀態的交換必須足夠充分；
- 溫度 \(T\) 的下降必須足夠緩慢。

退火過程的兩點啟示

Metropolis準則
- 如果 \(E(j)\le E(i)\)，則狀態轉換被接受；
- 如果 \(E(j)>E(i)\)，則狀態轉移被接受的概率為：\(e^{\frac{E(i)-E(j)}{KT}}\)

其中 \(i\) 是舊狀態，\(j\) 是新狀態。

當溫度緩慢趨于絕對0度時，系統以概率1達到內能最小狀態。

posted @ 2023-08-17 18:39 feixianxing 閱讀(69) 評論(0) 收藏舉報

刷新頁面返回頂部

feixianxing