組合問題由于其可能的解的數量十分龐大，無法用窮舉法求解最優解。局部搜索算法旨在減少復雜度的情況下尋找最優解，盡管其不一定能夠找到全局最優解，但是往往可以找到滿意的局部最優解。

局部搜索算法

組合問題由于其可能的解的數量十分龐大，無法用窮舉法求解最優解。

局部搜索算法旨在減少復雜度的情況下尋找最優解，盡管其不一定能夠找到全局最優解，但是往往可以找到滿意的局部最優解。

爬山法

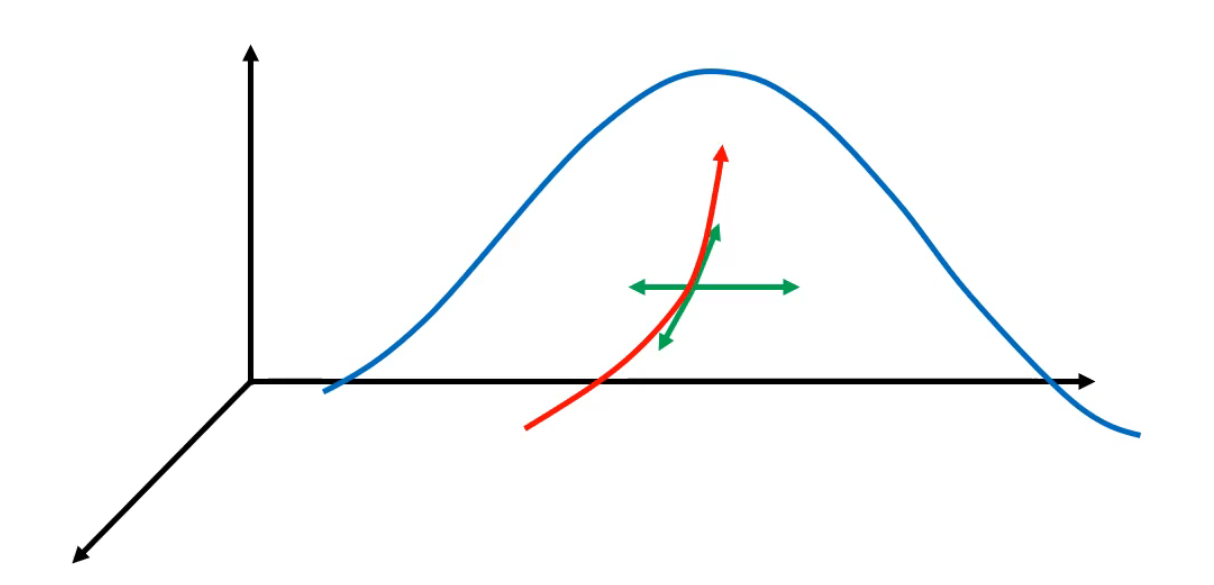
類似于盲人爬山，無法看到全局的景象，但是有拐杖可以探測臨近的區域。

每一次使用拐杖在周圍掃一圈，把這一圈上每一個點的高度與自己腳底的高度比較，找到距離腳底最高的那個點所在的方向前進。

重復以上過程。直到掃描周圍的一圈，發現都低于自己腳底的高度。

此時位于局部最高點。

核心思想

鄰域內找一個最優的結果，接受它，再以此為新的起點，重復這個過程。

領域的概念

上文中對于領域的現實類比案例是容易理解的， 但是在組合優化問題中，領域是指什么呢？

對解 \(S\) 經過一些簡單變換后，得到的另一個解稱作解 \(S\) 的鄰居，解 \(S\) 所有鄰居的集合稱作解 \(S\) 的鄰域。

鄰域舉例

• 皇后問題：每行每列有且只有一個皇后，每對角線至多一個皇后。

  \(S=\{S_i\}\) 表示一個可能解，其中 \(S_i\) 表示在第 \(i\) 行，第 \(S_i\) 列有一個皇后。

  如四皇后問題的一個解： \(S=(2, 4, 1, 3)\)

  

  任意交換兩個皇后的位置獲得一個解的鄰居，則\((2,4,1,3)\)的所有鄰居，也就是鄰域為：

  \(\{(4,2,1,3),(1,4,2,3),(3,4,1,2),(2,1,4,3),(2,3,1,4),(2,4,3,1)\}\)

• 旅行商問題

  • 常規交換法

    

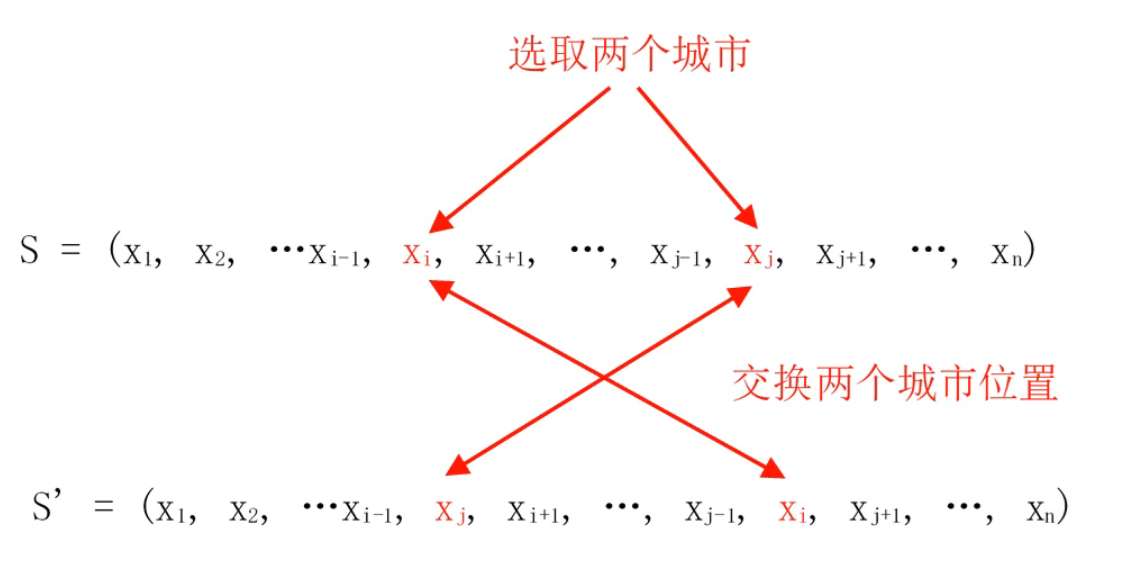
    序列 \(S\) 是對于 \(n\) 個城市的訪問順序，將其中兩個城市的訪問順序進行調換，則得到一個鄰居 \(S'\).

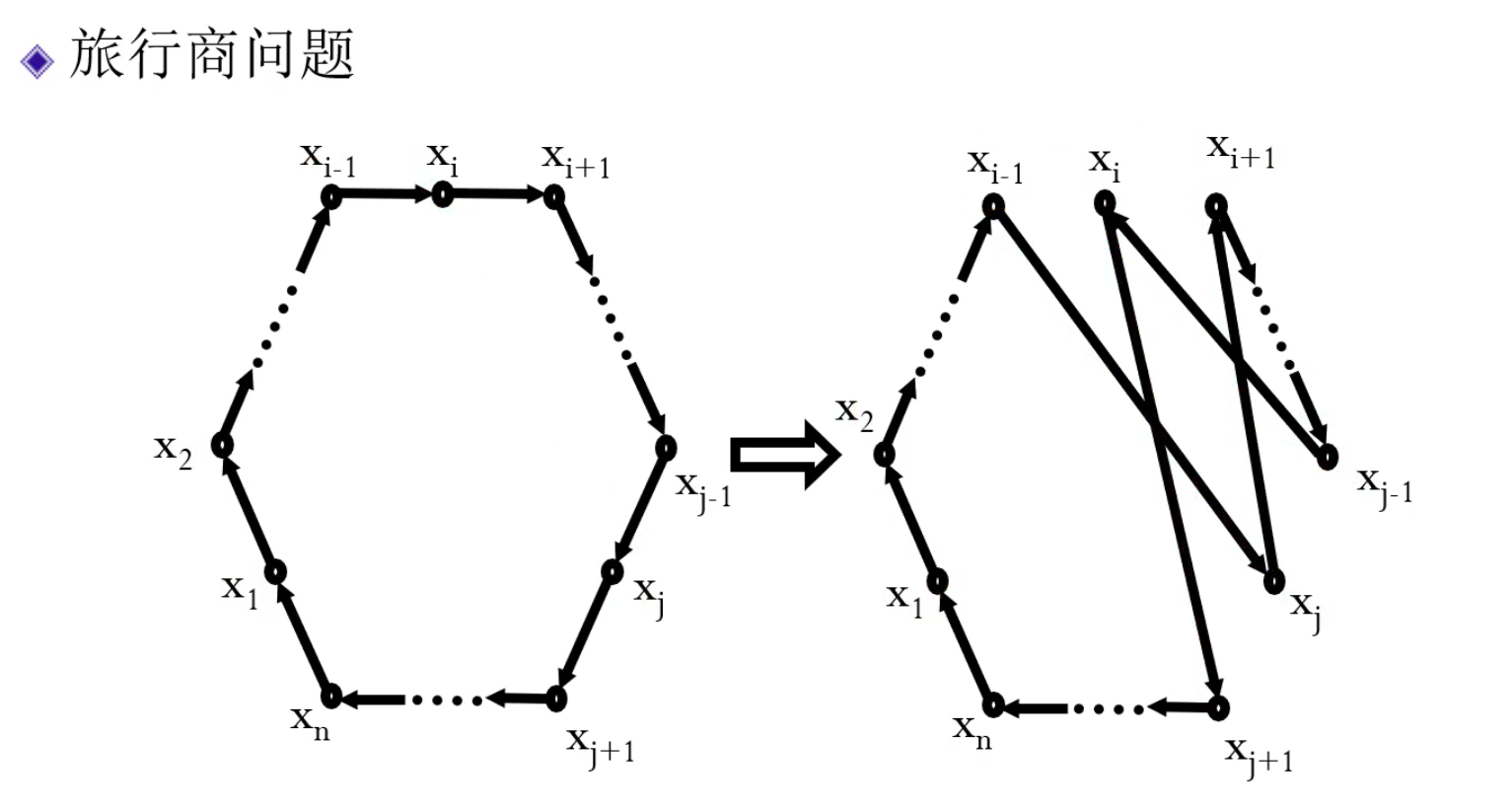
    常規交換法的路線改變示例圖：

    

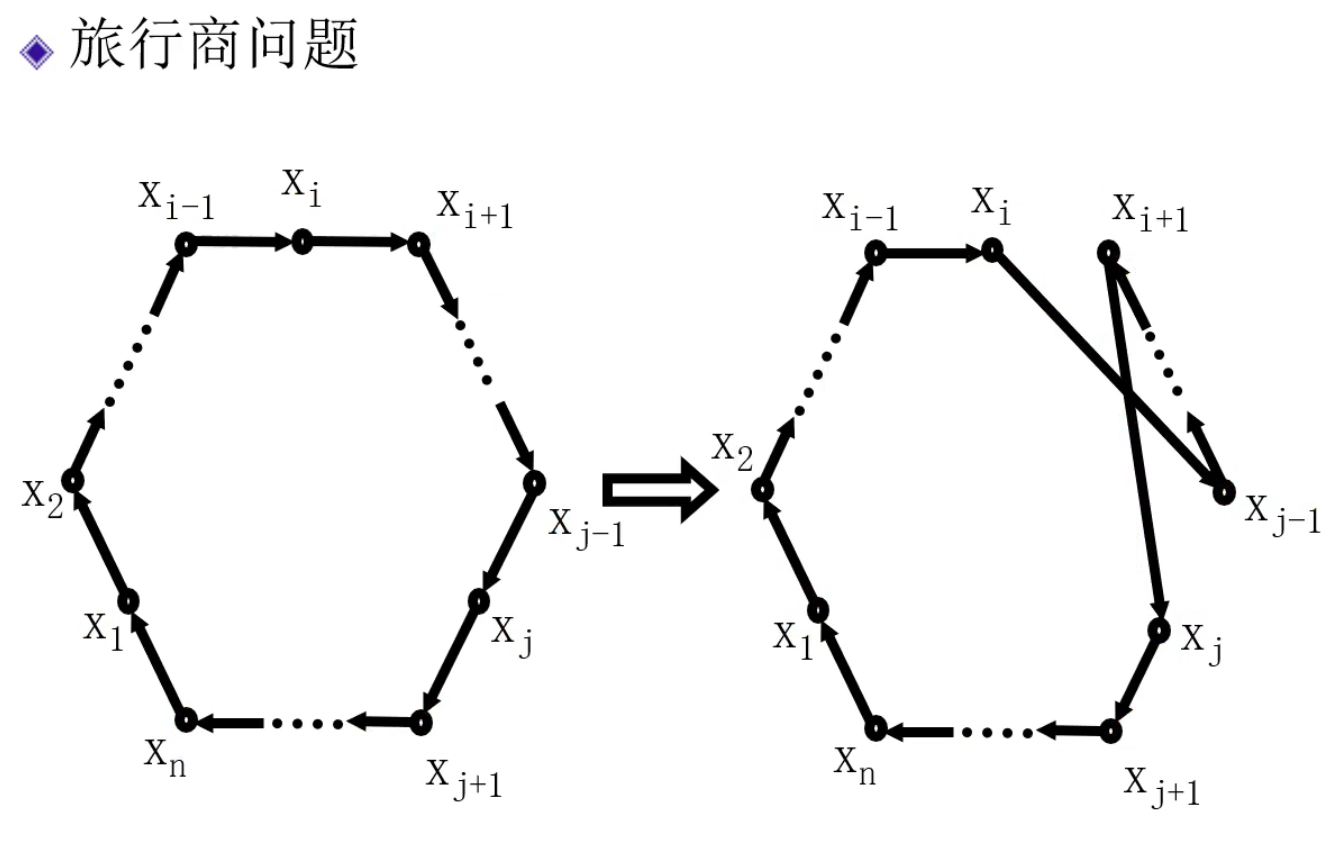
  • 逆序交換法

    

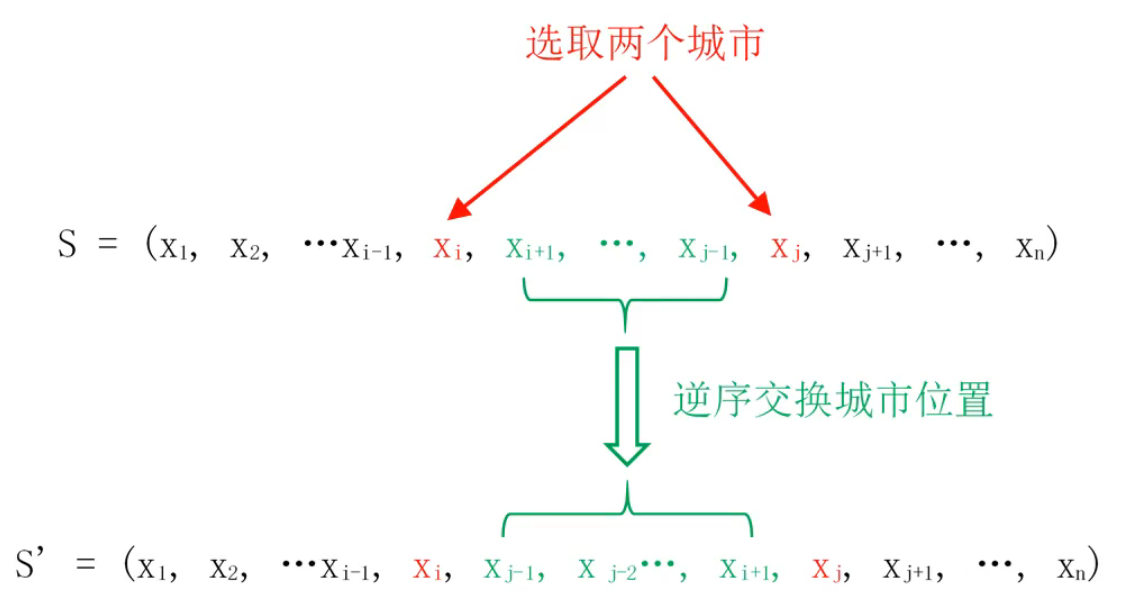
    選取兩個城市 \(x_i\) 和 \(x_j\) ，將這兩個城市之間的序列進行逆序操作。( \(x_i\) 和 \(x_j\) 是不變的 )

    逆序交換法的路線改變示例圖：

    

局部搜索算法描述

1. 隨機的選擇一個初始的可能解 \(x_0\in D\) ，\(x_b=x_0\) ，\(P=N(x_b)\) ；
2. 如果 \(P\) 不為空，則
3. Begin
4. ? 選擇 \(P\) 的一個子集 \(P'\) ，\(x_n\) 為 \(P'\) 中的最優解
5. ? 如果 \(f(x_n)<f(x_b)\)，則 \(x_b = x_n\)，\(P=N(x_b)\)，轉2；
6. ? 否則 \(P=P-P'\)，轉2.
7. End
8. 輸出計算結果
9. 結束

其中：

• \(N(x)\)函數用于獲取組合 \(x\) 的鄰域。

• 這里的算法比上文的爬山法更具一般性，沒有直接在領域中尋找局部最優解，而是在鄰域的子集中尋找最優解。

• \(f(x)\)用于計算并比較組合 \(x\) 的優良性，從而最終可以選出局部最優解。在旅行商問題中可以是路徑的長度，在0-1背包中可以是背包中物品的價格。