第六章習題
下面的機器數都以16進制表示
| w | func1(w) | func2(w) |
|---|---|---|
| 機器數 ; 值 | 機器數 ; 值 | 機器數 ; 值 |
| 0000007F;127 | 0000007F;127 | 0000007F;127 |
| 00000080;128 | 00000080;128 | FFFFFF80;-128 |
| 000000FF;255 | 000000FF;255 | FFFFFFFF;-1 |
| 00000100;256 | 00000000;0 | 00000000;0 |
兩個函數的功能:都是先將參數左移24位之后再右移24位;區別是func1是先移動完了再強制轉換,所以全程都是無符號數,采用邏輯右移;而func2左移完了之后先轉換再右移,所以采用算數右移
4.
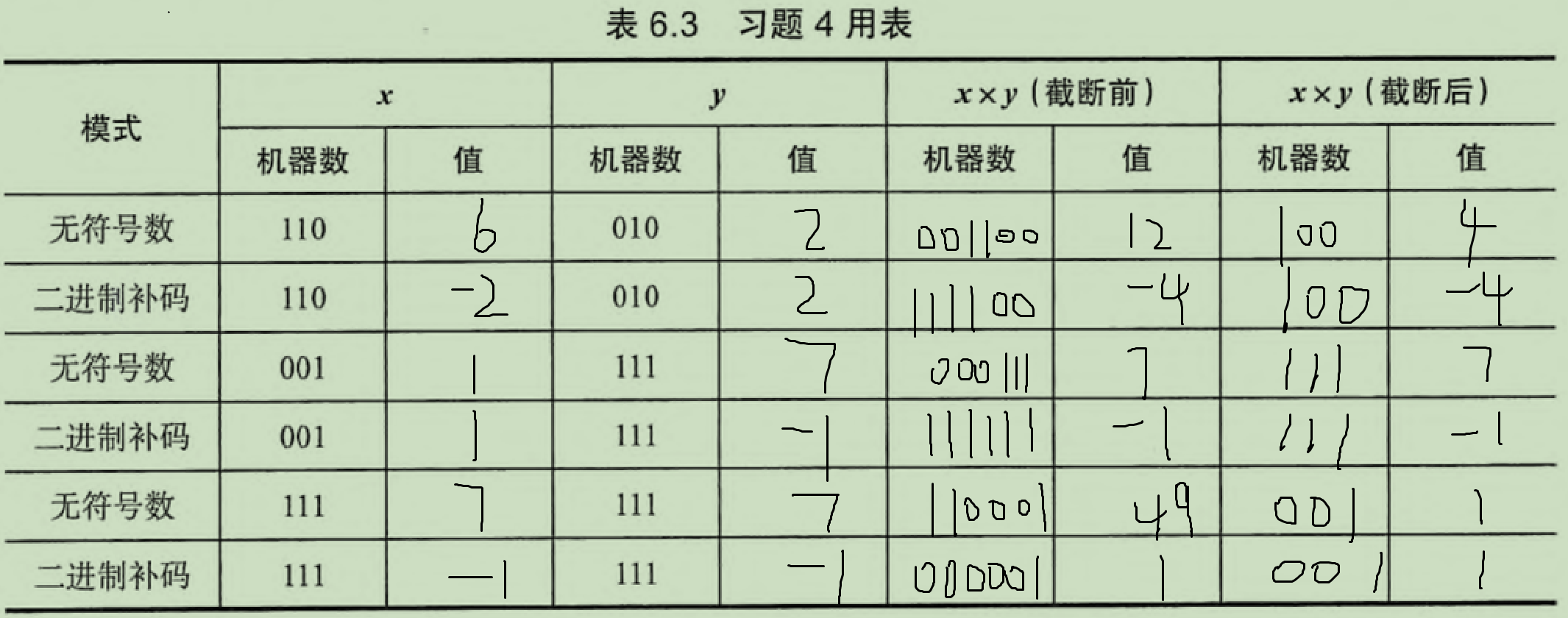
5.
通過分析反編譯的代碼可以發現x擴大了15倍,所以M為15;而y+=3的原因是為了向0取整,根據y>>=2可以得出N=4
6.
串行進位:
\[C_1 = A_1 C_0 + B_1 C_0 + A_1 B_1
\]
\[C_2 = A_2 C_1 + B_2 C_1 + A_2 B_2
\]
\[C_3 = A_3 C_2 + B_3 C_2 + A_3 B_3
\]
\[C_4 = A_4 C_3 + B_4 C_3 + A_4 B_4
\]
并行進位:
\[C_1 = A_1 B_1 + (A_1 + B_1) C_0
\]
\[C_2 = A_2 B_2 + (A_2 + B_2) A_1 B_1 + (A_2 + B_2)(A_1 + B_1) C_0
\]
\[\begin{aligned}
C_3 = & A_3 B_3 + (A_3 + B_3) A_2 B_2 + (A_3 + B_3)(A_2 + B_2) A_1 B_1 \\
& + (A_3 + B_3)(A_2 + B_2)(A_1 + B_1) C_0
\end{aligned}
\]
\[\begin{aligned}
C_4 = & A_4 B_4 + (A_4 + B_4) A_3 B_3 + (A_4 + B_4)(A_3 + B_3) A_2 B_2 \\
& + (A_4 + B_4)(A_3 + B_3)(A_2 + B_2) A_1 B_1 \\
& + (A_4 + B_4)(A_3 + B_3)(A_2 + B_2)(A_1 + B_1) C_0
\end{aligned}
\]
(1). 由題\([x+y]_{\text{補}}=0010,[x-y]_{\text{補}}=1000\),所以\(x+y=2,x-y=-8\)(溢出)
(2).
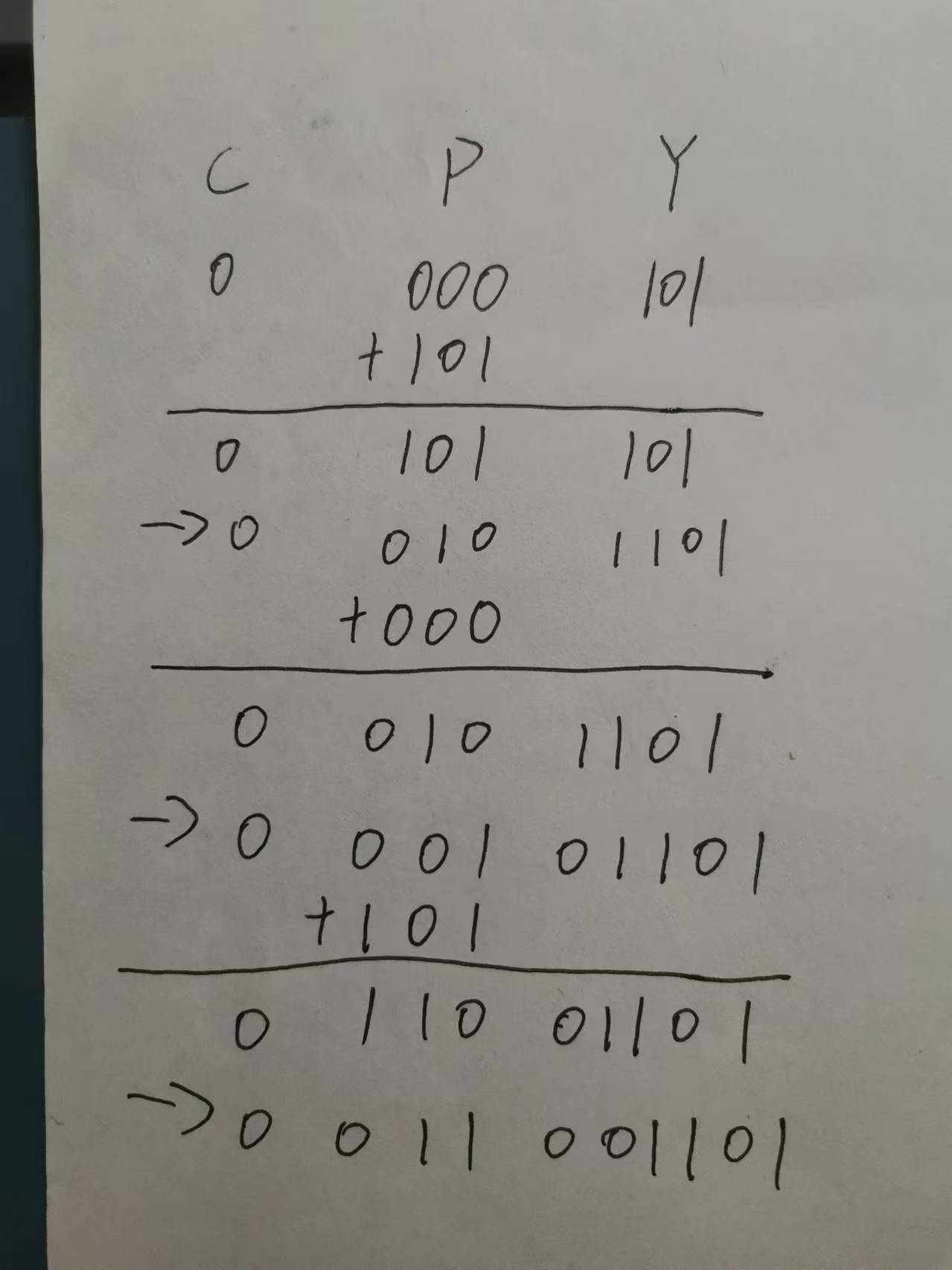
符號位單獨處理,可以知道為1,所以最后的原碼結果為\(10011001\),真值為\(-25\);由于\(P\)是一個非0數,所以溢出
(3).
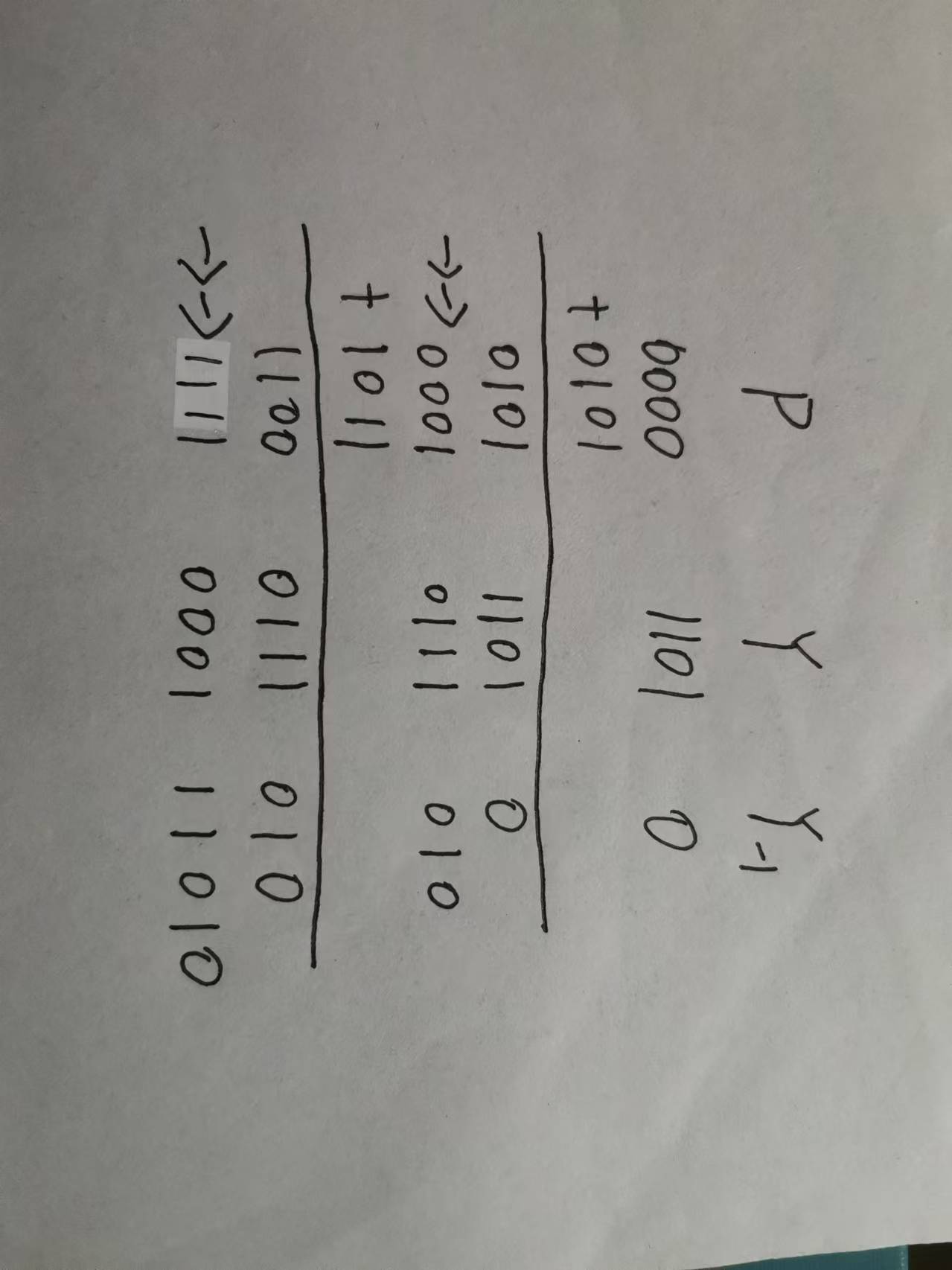
可以得到最后的補碼結果為\(11110001\),真值為\(-15\)
(4).
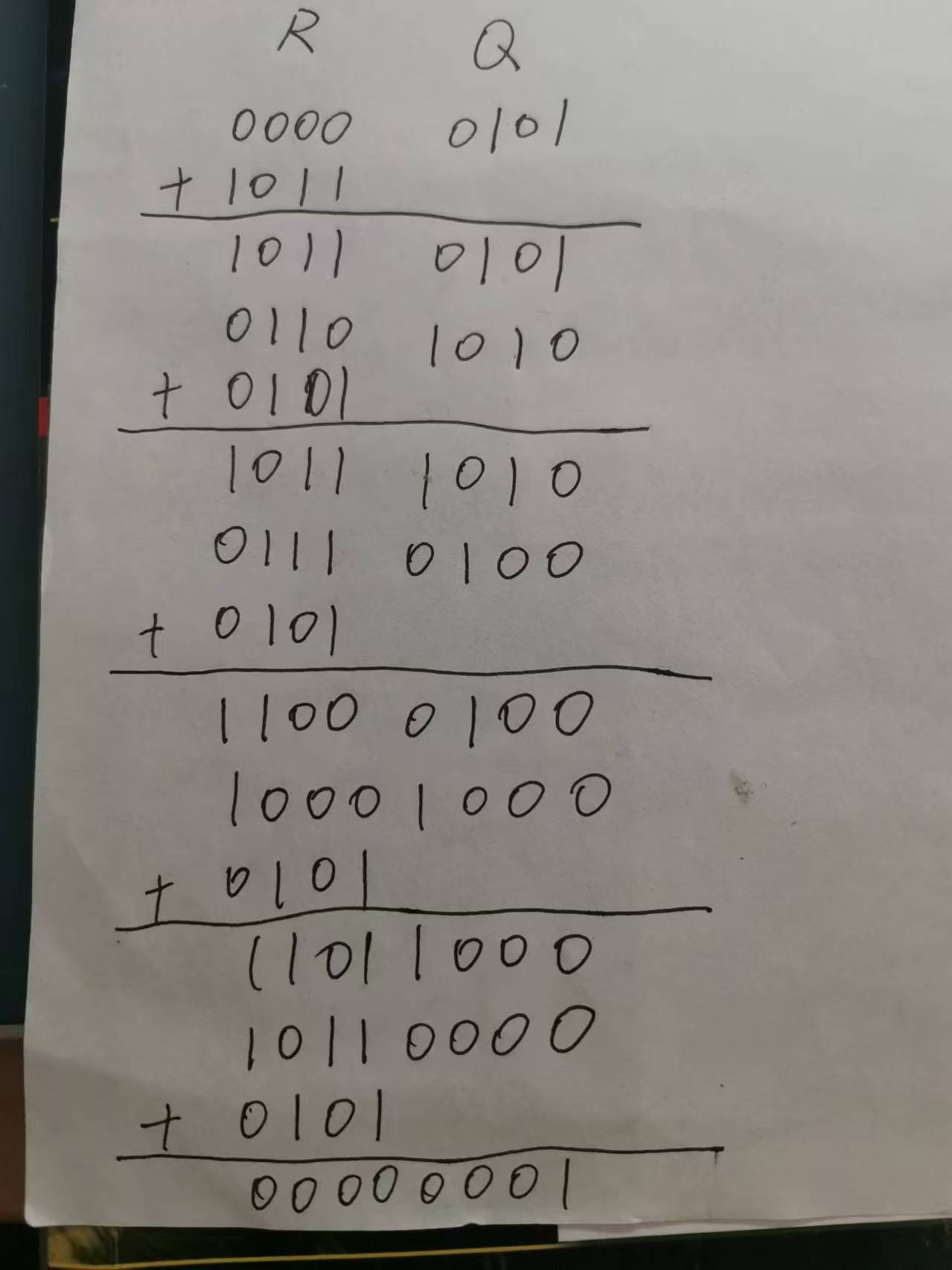
符號單獨處理,可以得到結果為商為-1余為0
(5).

最后修正商,可得商為1111,真值為-1;不用修正余數,為0010,真值為2
11
(4).
x = (15/16) × 2?,y = (2/16) × 2?。運算為 x - y
- 將 x 和 y 表示為規定的浮點數格式
- x
- 尾數: 15/16 = (0.1111)?。其 6 位補碼表示為
00.1111 - 階碼: 5。其 4 位移碼表示為 5 + 8 = 13 = (1101)?
- 所以,x =
1101,001111
- 尾數: 15/16 = (0.1111)?。其 6 位補碼表示為
- y
- 尾數: 2/16 = 1/8 = (0.001)?。其 6 位補碼表示為
00.0010 - 階碼: 7。其 4 位移碼表示為 7 + 8 = 15 = (1111)?
- 所以,y =
1111,000010
- 尾數: 2/16 = 1/8 = (0.001)?。其 6 位補碼表示為
- x
接下來,需要對階,使兩個數的階碼相等。選擇較大的階碼 7 作為公共階碼。x 的階碼需要從 5 調整到 7,因此 x 的尾數需要右移 2 位
- 情況一:不采用任何附加位
-
對階:
- x 的尾數
00.1111右移 2 位 - 移位后,x 的尾數變為
00.0011(最后兩位11丟失) - x 的階碼變為 7
- x 的尾數
-
尾數相加:
00.0011(x 的尾數) +11.1110(-y 的尾數) =00.0001
-
規格化:
- 結果
00.0001的符號位與最高數值位不同,需要規格化 - 尾數左移 3 位變為
00.1000 - 階碼相應地減 3,即 7 - 3 = 4
- 結果
-
得出結果:
- 規格化后的尾數為
00.1000,階碼為 4 - 其值為: (0.1000)? × 2? = (1/2) × 16 = 8
- 規格化后的尾數為
-
計算結果為 8
-
情況二:采用 2 位附加位 (保護位 G,舍入位 R)
-
對階:
- x 的尾數
00.1111附加兩位00,變為00.1111 00 - 右移 2 位后,尾數部分變為
00.0011,保護位 G = 1,舍入位 R = 1
- x 的尾數
-
尾數相加:
- 將 x 的對階后尾數與 -y 的尾數相加 (運算時包含附加位):
00.0011 11 + 11.1110 00 ----------------- 00.0001 11 - 結果的尾數部分為
00.0001,G = 1,R = 1。階碼為 7
- 將 x 的對階后尾數與 -y 的尾數相加 (運算時包含附加位):
-
規格化:
- 結果
00.0001 11需要規格化 - 尾數左移 3 位,變為
00.1110 00 - 階碼相應地減 3,即 7 - 3 = 4
- 規格化后,尾數為
00.1110,G = 0,R = 0
- 結果
-
舍入:
- 根據“就近舍入到偶數”規則,檢查 G、R 和 S (粘位,此處為0) 的值
- 由于 G=0,表示移出的值小于最低有效位的一半,因此執行向下舍入 (即截斷)
- 舍入后的尾數仍為
00.1110
-
得出結果:
- 最終尾數為
00.1110,階碼為 4 - 其值為: (0.1110)? × 2? = (1/2 + 1/4 + 1/8) × 16 = (7/8) × 16 = 14
- 最終尾數為
-
計算結果為 14



 浙公網安備 33010602011771號
浙公網安備 33010602011771號