整形算術單元容易預測實現硬件行為，而浮點單元由于 （1）不遵守結合律（2）rounding 模式和特殊情況處理（subnormal、nan、-0、+inf、-inf） 往往更難預測硬件計算結果。神經網絡中運算 MAC 運算累加超長數組同時涉及 (1) 和 (2) 問題，不滿足交換律使得遍歷保證 100% 和算法（GPU 結果）一致近乎不可能，且常見深度學習庫中為了減少累加誤差往往在更高精度進行累加，涉及層層 GPU 軟件棧選項使得對齊更加困難^[1]；而 element-wise 運算只涉及數值計算，理論只最多需要遍歷 2**32 種組合存在對齊可能性。

根據 CUDA 文檔^[2]浮點運算特性可通過編譯器選項控制，默認編譯選項遵循 IEEE-754 round to nearest。GPU 算術支持配置選項如下：

• FTZ, Flush to Zero, 將 subnormal 舍入到 0，編譯器選項控制
• Fast Div，快速近似除法，編譯器選項控制
• Fast Sqrt，快速近似開方，編譯器選項控制
• rounding mode ，代碼層面控制

根據選項猜測 GPU 算術單元輸入端口包含一個表示舍入模式，一個控制除法/開方迭代次數上限，而 FTZ 可能是在算術模塊之外通過識別為 0 更改 sparsity 進而調度算術模塊的輸入數據。

雖說 IEEE-754 是一個參數化的定義，但畢竟 bf16 并不屬于 IEEE-754 預定義的浮點格式，上周對 GPU element-wise bf16 浮點運算做了點小實驗觀察 GPU 算術行為，實驗環境是 RTX Mobile 4060 + pytorch 2.2/CUDA 12.1。中科院開源fudian模塊可以參數化生成浮點算術模塊，但僅在 float32/double64 上進行測試滿足 IEEE-754 標準^[3]。其中除法模塊中間迭代位寬在 bf16 設置下會報錯無法編譯，乘法、加法模塊可以正常編譯通過。在 BF16/RNE 配置下遍歷測試乘法計算 RTL 和 GPU 結果，得到結果十分有趣：

• 負 0 處理：Fudian 在 bf16 模式配置無法處理 -0 計算，-0 * 0 會輸出 nan，-0 * inf 會輸出 0 （因為浮點中的 0 可能是舍入后的 0 而非真 0，所以 IEEE-754 規定 0 乘 inf 應當是 inf），而 GPU 表現符合 IEEE-754 標準；
• NaN：即使同時 NaN 的輸出，由于 NaN 有多種 bit 表示，二者數值也不相同。這部分在后文分析時假設 NaN 分析假設相同了，且 NaN 在測試集中肯定屬于少數；
• 舍入：Fudian 部分計算和 GPU 能保持每一個bit 相同即 bit-accuracy，有意思的是保持一致的部分呈現高度的規律性，假設固定兩個 bf16 輸入的其中一個輸入 A，遍歷另一個輸入 B，那么保持 bit-accuracy 的數值范圍大致在 B 一個對稱的區間，這個 B 的起點和大小隨著 A 的值變化，大致范圍在 40~60% 左右。也就是說只有大致一半的結果 Fudian 能和 GPU BF16 乘法保持一致。

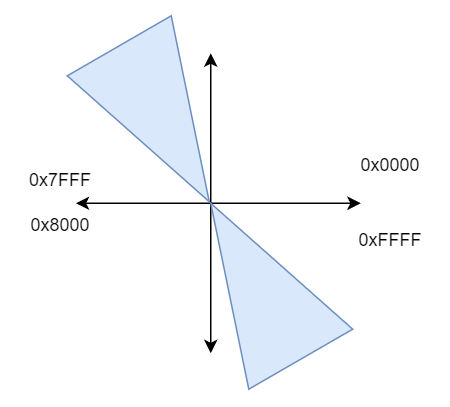
具體挑了一個對不上的例子，結果如下：

可見二者僅在 mantissa 相差 1 的舍入誤差，遵循 IEEE-754 BF16 究竟是 0x2181 還是 0x2180 呢？A、B十進制數值分別是 -9.1835e-41 和 -9.51852e+20，GPU 計算結果是 8.74138e-20，Fudian 計算結果是 8.6736174e-20，而理論值應是 8.7413328420e-20。GPU 的計算結果與理論值誤差更小，似乎此時 GPU 遵循了 IEEE-754 而 Fudian 和 IEEE-754 存在出入。