狀壓 dp
狀壓dp
簡介
狀壓 \(dp\) 就是把每個元素是否存在于一個集合中的情況用一個 二進制數表示,來作為 \(dp\) 的一個階段,通常我們會利用計算機超快的位運算對這個集合進行操作。
狀壓 \(dp\) 主要分為以下兩類:
1.集合類
2.棋盤類(輪廓線 \(dp\))
其中,集合類中有一類叫做子集枚舉,會在后文講到
集合類
luogu P10447 最短 Hamilton 路徑
此題為經典的 \(NP\) 問題——旅行商問題,\(NP\) 問題沒有多項式的復雜度解法
思路:
不難想到純暴力解法:
求出 \(n\) 個點的全排列,每個全排列就是一條路徑,一共 \(n!\) 條路徑,每條路徑計算距離總和需要加 \(n\) 次,復雜度為 \(O(n \times n!)\)。
題目中 \(n \le 20\),最多 \(20*20!=48,658,040,163,532,800,000 \approx 4.9 \times 10^{19}\),不難發現直接升天了,所以我們需要更好的解法。
定義 \(f_{i,s}\) 表示最后一個走到的點是 \(i\)(下標從 \(0\) 開始),已經走過的點所構成的集合二進制為 \(s\) 時,所走的最小距離。
轉移(刷表法):后文的公式都是用以數學的表示法寫的,具體的代碼表示請看代碼
初始化:\(f_{0,1}=0\)
答案:\(f_{n-1,2^n-1}\)
復雜度:一共會遍歷 \(2^n\) 個集合狀態,每個狀態要枚舉 存在以及不存在 \(s\) 中的點,為 \(n^2\),總復雜度:\(O(n^2 \times 2^n)\),當 \(n=20\) 時,\(20^2 \times 2^{20}=419,430,400 \approx 4 \times 10^8\),能夠接受,然后就過了。
代碼:
#include<bits/stdc++.h>
using namespace std;
const int N=20;
int n,ans=0x3f3f3f3f,dis[N][N],f[N][1<<N];
int main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>dis[i][j];
}
}
memset(f,0x3f,sizeof(f));
f[0][1]=0;
for(int s=1;s<1<<n;s++){
for(int i=0;i<n;i++){
if(s&(1<<i)) continue;//找一個不在 s 中的點 i
for(int j=0;j<n;j++){
if(!(s&(1<<j))) continue;//找一個在 s 中的點 j
f[i][s|(1<<i)]=min(f[i][s|(1<<i)],f[j][s]+dis[j][i]);
}
}
}
cout<<f[n-1][(1<<n)-1];
return 0;
}
luogu P1433 吃奶酪
幾乎一樣,只是初始化和答案略微不同
代碼:
#include<bits/stdc++.h>
using namespace std;
const int N=15;
int n;
double ans,x[N],y[N],d[N][N],f[N][1<<N];
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>x[i]>>y[i];
for(int i=0;i<n;i++){
for(int j=0;j<(1<<n);j++){
f[i][j]=10000000.0;
}
}
ans=10000000.0;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
d[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//預處理任意兩點間的距離
}
}
for(int i=0;i<n;i++){
f[i][1<<i]=sqrt(x[i]*x[i]+y[i]*y[i]);//初始化:從(0,0)走到(x_i,y_i)
}
for(int s=0;s<1<<n;s++){
for(int i=0;i<n;i++){
if((s&(1<<i))==0) continue;
for(int j=0;j<n;j++){
if(s&(1<<j)) continue;
f[j][s|(1<<j)]=min(f[j][s|(1<<j)],f[i][s]+d[i][j]);
}
}
}
for(int i=0;i<n;i++) ans=min(ans,f[i][(1<<n)-1]);//以任意點為結尾都可以
printf("%.2lf",ans);
return 0;
}
接下來是兩道 \(CF\) 的題(給出洛谷的鏈接,提交需至\(CF\))
AT_dp_o Matching
本題只需將任意一個性別作為集合即可,這里以所有女性為集合:
為了方便,記 \(cnt_s\) 表示 \(s\) 在二進制表示下的 \(1\) 的個數,題目中的好感度用 \(a_{i,j}\) 表示第 \(i\) 個男性與第 \(j\) 個女性的好感度:
定義 \(f_{i,s}\) 表示到第 \(i\) 個男性,且女性集合為 \(s\) 時的完美配對的總方案數
首先要明確一點,男性的順序是沒關系的,所以,我們可以假設到第 \(i\) 個男性就已經配對了 \(i\) 對男女,所以要求 \(cnt_s=i\) 時,才可以轉移
轉移:
事實上,我們可以用滾動數組滾掉 \(i\) 這一維,所以,轉移變為:
這里用 \(a_{cnt_s,j}=1\) 是因為當 \(s\) 確定時,\(cnt_s\) 就唯一確定了,不用再去遍歷 \(i\) 了
初始化:一個女性都沒有的方案數為 \(1\):\(f_0=1\)
答案:所有 \(n\) 對男女都已配對:\(f_{2^n-1}\)
這里再多說一句:C++ 的 STL 中有 __builtin_popcount(s) (注意,最前面是兩個 "_")表示 \(s\) 在二進制表示下的 \(1\) 的個數,即上文的 \(cnt_s\),復雜度為常數很大的 \(O(1)\),但其實沒太大必要,手寫一個求 \(cnt_s\) 的函數也沒多難,復雜度為 \(O(logn)\)
記得取模!!!
代碼:
#include<bits/stdc++.h>
using namespace std;
const int N=21,mod=1e9+7;
int n,a[N][N],f[1<<N];
int main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>a[i][j];
}
}
f[0]=1;
for(int s=0;s<(1<<n);s++){
int cnt=0,z=s;
while(z) cnt+=z&1,z>>=1;
for(int i=0;i<n;i++){
if(!(s&(1<<i))&&a[cnt][i]){
f[s|(1<<i)]=(f[s|(1<<i)]+f[s])%mod;
}
}
}
cout<<f[(1<<n)-1];
return 0;
}
AT_dp_u Grouping
這是一道 子集枚舉 的板題,題目十分簡單,但是需要介紹一下子集枚舉,先說本題思路,再介紹子集枚舉。
思路:
定義 \(f_S\) 表示選的兔子分成若干個組,這些兔子構成的二進制集合為 \(S\) 的最大得分
轉移:
初始化:
答案:\(f_{2^n-1}\)
以上為本題思路,接著介紹子集枚舉:
子集枚舉
代碼思路
從剛才的轉移方程來看,我們要枚舉 \(S\) 的所有子集 \(T\),才能進行狀態轉移,代碼怎么實現?
有一個很巧妙的方法:for(int T = S ; T >= 0 ; T = (T-1) & S)
分析一下,首先,代表 \(T\) 的二進制數肯定比代表 \(S\) 的二進制數小,由子集的性質顯然可知,所以初始 T=S,接著 \(T\) 肯定要不小于零,所以 T>=0。
最后是最重要的一步,我們已經知道了 \(T\) 肯定比 \(S\) 小,所以可以先讓 \(T--\),但不難發現,要是 \(S=(110)_2\),令T=S, T--,\(T\) 就會變成 \((101)_2\),顯然不是 \(S\) 的子集,怎么辦呢?
只要 \(T\&=S\) 就好了,因為 \(\&\) 的性質,所以 \(T\) 就會變成只含 \(S\) 中的樣子,剛才的例子就會變成:\(T=(100)_2\),所以就有了 \(T=(T-1)\&S\)
復雜度:\(O(3^n)\)
證明很有趣:
\(n\) 個數,先枚舉其所有的集合,可以分為元素個數分別為 \(0,1,2,3...n\) 的集合,對于每種大小為 \(k\) 的集合,我們記為 第 \(k\) 類集合(作者自己編的名字),相當于從 \(n\) 個數中選了 \(k\) 個數,所以有 \(C_{n}^{k}\) 種選擇,即第 \(k\) 類集合有這么多個
接著,對于每個第 \(k\) 類集合,它的子集個數一共有 \(2^k\) 個,所以,第 \(k\) 類集合一共要枚舉 \(C_{n}^{k} \times 2^k\) 個子集,那么對于 \(k \in [0,n]\),一共要枚舉的子集數就為:
不難發現,我們給原式湊了一個 \(\times 1^{n-k}\) 以后,原式的值不變,但是最后面的式子變成了我們所熟悉的 二項式定理,所以:
故復雜度為 \(O(3^n)\)
最后給出本題代碼:
代碼:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=16;
int n;
ll a[N][N],f[1<<N];
int main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>a[i][j];
}
}
for(int s=0;s<(1<<n);s++){
for(int i=0;i<n;i++){
for(int j=0;j<i;j++){
if((s&(1<<i))&&(s&(1<<j))) f[s]+=a[i][j];//初始化
}
}
}
for(int s=1;s<(1<<n);s++){
for(int t=s;t;t=(t-1)&s){//子集枚舉
f[s]=max(f[s],f[t]+f[s^t]);
}
}
cout<<f[(1<<n)-1];
return 0;
}
棋盤類(輪廓線dp)
首先,要知道,什么是輪廓線?
這里直接給出板題,方便解釋:
luogu P1896 [SCOI2005] 互不侵犯
眾所周知,經典的八皇后問題用到了 \(dfs\) 求解(luogu P1219 [USACO1.5] 八皇后 Checker Challenge),本題的限制要求和八皇后很像,但還是有很大區別,八皇后問題是求皇后的擺放方案,而本題是求合法方案數并且由于皇后和國王的走法不同,導致前者需用 \(dfs\) 求解,而后者可用狀壓 \(dp\) 求解。
給出下圖:
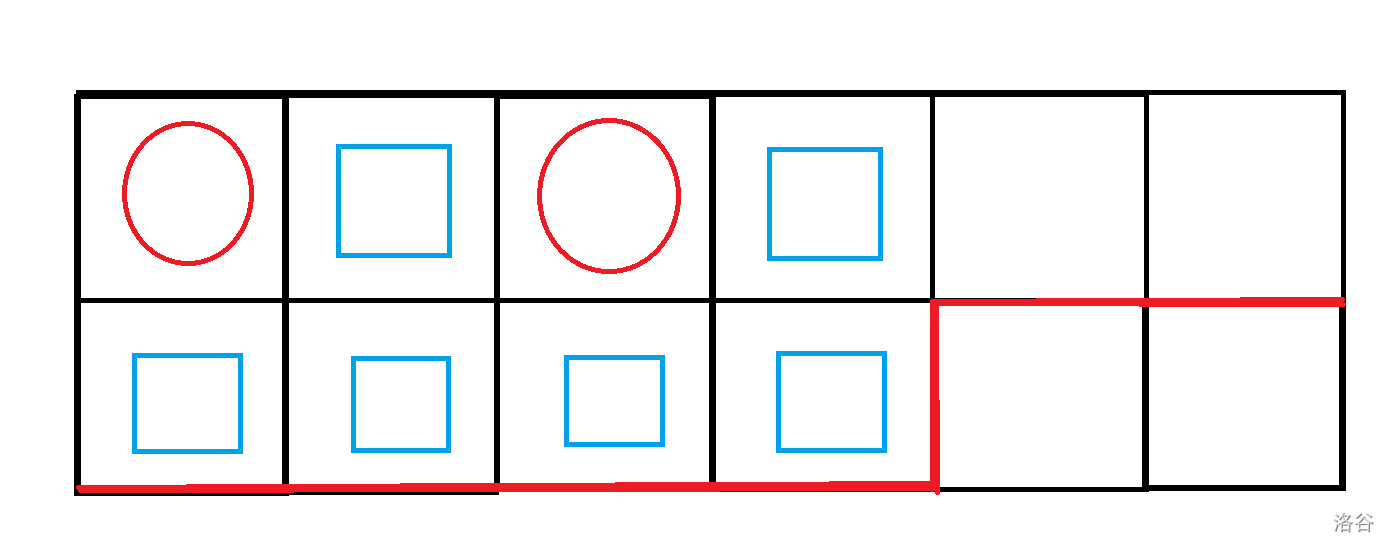
上圖中,紅色圓圈表示放了國王的位置,藍色方塊表示國王的攻擊范圍(即不能放國王的位置),紅色的折現就是下一個國王能放的位置的邊界(要在紅線的下面或右邊),因此,紅線就是輪廓線。輪廓線 \(dp\) 的階段是行的編號,\(狀態就是輪廓線\)。
不難發現,我們可以用一個 二進制數表示第 \(i\) 的輪廓線(第 \(j\) 表示的就是從右往左數第 \(j\) 個格子是否能放新的國王,這里的 \(j\) 是從 \(0\) 開始的)
所以,我們有了動規的的狀態:
定義 \(f_{i,s,j}\) 表示第 \(i\) 行,這一行的輪廓線為 \(s\) ,且已經放了 \(j\) 個國王的方案數
轉移:
上面的方程中,\(t\) 表示上一行的輪廓線,而 t&s==0 表示第 \(i\) 行的輪廓線 \(s\) 與上一行的輪廓線 \(t\) 沒有沖突,即國王沒有互相沖突,\(c\) 表示到了上一行已經放了 \(c\) 個國王,這里有點類似背包
初始化:一個國王都沒放:\(f_{0,0,0}=1\)
答案:
因為我們不知道最后一行會擺成什么樣子,所以要遍歷最后一行的所有輪廓線,然后求和。
但是其實,上述的說法有問題。嚴格來說,我們枚舉的 \(s\) 和 \(t\) 并不是輪廓線,而是每一行的國王擺放的情況,只不過,t&s==0 的這個條件,讓相當于求出了輪廓線,這里需要注意,但是上文就這樣吧,下文會改變說法的
然后本題就做完了,但別著急,對于這種輪廓線,我們有優化:
不難發現,對于同一行的狀態 \(s\) ,有些肯定不合法,例如 \((1101101)_2\),(\(1\) 表示放了國王)很明顯,按照題意,是不允許同一行的國王相鄰的(事實上是八連通范圍內都不能相鄰),所以,我們可以在開始時,先處理出來所有可能的狀態 \(s\),即把所以有相鄰 \(1\) 的 \(s\) 全部去掉,接著每行的狀態只需枚舉預處理出的合法的 \(s\) 即可。
這樣,我們就優化了時間,此時,\(f_{i,s,j}\) 中的 \(s\) 表示為第 \(s\) 個可行的狀態 \(s\),事實上,空間的話,可以輸出一下當 \(n=9\) 時,可行的 \(s\) 數,然后 \(f\) 數組的第二維開那么大就好了,這里直接給出,\(n=9\) 時,合法的狀態數為 \(89\),和 \(2^9=512\) 差了一個數量級,當然,本題就算開了 \(2^9\) 也不會 \(MLE\),所以代碼中直接開了 \(2^9\) 大小的數組。
下面給出的是刷表法,跟上面的填表法幾乎一樣(狀壓還是刷表更好)
還有一點要說,預處理時怎么判斷 \(s\) 是否合法?即 \(s\) 的二進制表示是否有相鄰的 \(1\)?只需判斷 \(s \&(s>>1)\) 和 \(s \& (s<<1)\) 是否都為 \(0\) 即可!
代碼:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=9;
int n,k,cnt,ok[1<<N],cnts[1<<N];//用ok數組記錄可行的s,cnts數組記錄該可行狀態s二進制下1的個數,即這種狀態放了cnts個國王
ll f[N+1][1<<N][N*N+1],ans;
void init(){
for(int s=0;s<1<<n;s++){
if((s&(s<<1))||(s&(s>>1))) continue;//不合法
ok[cnt]=s;
int z=s;
while(z) cnts[cnt]+=1&z,z>>=1;
cnt++;
}
}
bool is(int a,int b){//判斷兩行的狀態是否沖突
return (a&b)||((a<<1)&b)||((a>>1)&b);
}
int main(){
cin>>n>>k;
init();//預處理所有的合法狀態
f[0][0][0]=1;
for(int i=0;i<n;i++){
for(int j=0;j<cnt;j++){
for(int r=0;r<cnt;r++){
if(is(ok[j],ok[r])) continue;
for(int c=0;c<=k;c++){
if(cnts[r]+c>k) continue;
f[i+1][r][cnts[r]+c]+=f[i][j][c];
}
}
}
}
for(int i=0;i<cnt;i++) ans+=f[n][i][k];
cout<<ans;
return 0;
}
luogu P1879 [USACO06NOV] Corn Fields G
來一道練習題,但有點不一樣,本題給出一張地圖,有些點不能放奶牛,怎么辦?有個巧妙的方法,對于第 \(i\) 行給出的輸入,記 \(t_i\) 在二進制下表示該行的空地和草地的情況,空地就讓二進制的那一位為 \(1\),草地就為 \(0\)。枚舉第 \(i\) 行的奶牛的擺放狀態時若 (t[i]&ok[j])!=0,則說明,有奶牛在空地上,不合法,就跳過
代碼:
#include<bits/stdc++.h>
using namespace std;
const int N=12,mod=1e8;
int n,m,cnt,ans,t[N+1],f[N+1][1<<N],ok[1<<N];//本題不用 cnts 數組,放幾頭奶牛都可以
void init(){
for(int s=0;s<1<<m;s++){
if((s&(s<<1))||((s>>1)&s)) continue;
ok[++cnt]=s;
}
}
int main(){
cin>>n>>m;
init();//依舊預處理所有可行的狀態s
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
int k;
cin>>k;
t[i]=t[i]<<1|(1-k);
}
}
for(int i=1;i<=cnt;i++) if(!(ok[i]&t[1])) f[1][i]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=cnt;j++){
if(ok[j]&t[i-1]) continue;
for(int k=1;k<=cnt;k++){
if((ok[j]&ok[k])||(ok[k]&t[i])) continue;
f[i][k]=(f[i][k]+f[i-1][j])%mod;
}
}
}
for(int j=1;j<=cnt;j++) ans=(ans+f[n][j])%mod;
cout<<ans;
return 0;
}
luogu P2704 [NOI2001] 炮兵陣地
本題是前幾題的綜合,很有價值,既要預處理所有合法的狀態 \(s\),還要預處理每個 \(s\) 的二進制下 \(1\) 的個數,以及空間和時間優化。
本題要看前兩行的狀態,所以定義 \(f_{i,s1,s2}\) 表示到了第 \(i\) 行,這一行狀態為 \(s1\),上一行狀態為 \(s2\) 的最多能放的炮兵數。
用 \(is1(i,s)\) 表示狀態 \(s\) 是否能滿足第 \(i\) 行的地形,不滿足返回\(true\),\(is2(s1,s2,s3)\) 表示 \(s1\),\(s2\) , \(s3\) 是否有至少有兩個是沖突的,沖突則返回 \(true\)。\(cnt_{s}\) 表示 \(s\) 在二進制表示下 \(1\) 的個數
轉移:
答案:
初始化,需要初始化第一行和第二行,具體實現的看代碼吧,這里就不寫出來了
注意,本題有 \(hack\) 數據:\(n=1\) ,需要特判。還有,直接開\(f[100][1<<10][1<<10]\) 就算是 \(int\) 也會 \(MLE\),所以這就要用到上文提到的只開合法的狀態的數量大小,需要自己在本地輸出一下最大的數量,然后開那么大,開 \(65\) 是夠用的
代碼:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=10;
int n,m,cnt,ok[1<<N],t[105],cnts[1<<N],ans,f[105][65][65];
void init(){
for(int s=0;s<1<<m;s++){
if((s&(s>>2)||(s&(s>>1)))) continue;
ok[++cnt]=s;
int z=s;
while(z) cnts[cnt]+=1&z,z>>=1;
}
}
int main(){
cin>>n>>m;
init();//依舊可以預處理所有合法狀態
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
char c;
cin>>c;
t[i]=t[i]<<1|(c=='P'?0:1);
}
}
for(int i=1;i<=cnt;i++){
if(ok[i]&t[1]) continue;
f[1][i][0]=cnts[i];//預處理第一行
ans=max(f[1][i][0],ans);//處理n=1時的情況
if(ok[i]&t[1]) continue;
for(int j=1;j<=cnt;j++){
if(ok[j]&t[2]) continue;
if(ok[i]&ok[j]) continue;
f[2][j][i]=cnts[i]+cnts[j];
}
}
for(int i=1;i<=n;i++){
for(int s1=1;s1<=cnt;s1++){
if(ok[s1]&t[i]) continue;
for(int s2=1;s2<=cnt;s2++){
if(ok[s2]&t[i+1]) continue;
if(ok[s1]&ok[s2]) continue;
for(int s3=1;s3<=cnt;s3++){
if(ok[s3]&t[i+2]) continue;
if(ok[s1]&ok[s3]) continue;
if(ok[s2]&ok[s3]) continue;
f[i+2][s3][s2]=max(f[i+2][s3][s2],f[i+1][s2][s1]+cnts[s3]);
}
}
}
}
for(int i=1;i<=cnt;i++){
for(int j=1;j<=cnt;j++){
if(ok[i]&t[n]) continue;
if(ok[j]&t[n-1]) continue;
if(ok[i]&ok[j]) continue;
ans=max(ans,f[n][i][j]);
}
}
cout<<ans;
return 0;
}
最后,給出幾道練習題:
luogu P3112 [USACO14DEC] Guard Mark G
luogu P2915 [USACO08NOV] Mixed Up Cows G
今天先更到這里,之后會繼續做狀壓 \(dp\),遇到好題會繼續寫的,qwq。


 浙公網安備 33010602011771號
浙公網安備 33010602011771號