KMP

今日2025.10.17

成功又開通了博客園，以后就在這里寫了

簡介

\(KMP\) 由 \(D.E.Knuth\)，\(J.H.Morris\) 和 \(V.R.Pratt\) 提出的，用于解決單模式串與主串匹配問題，是十分優秀且巧妙的算法（事實上，字符串的算法都很巧妙）

問題

給定一個長度為 \(n\) 的主串 \(s\)，和一個長度為 \(m\) 的模式串 \(p\)，\(n,m≤1e6\)，詢問 \(p\) 是否為 \(s\) 的子串。

暴力算法：

定義兩個指針 \(i,j\)，分別指向 \(s,p\)（從下標 \(0\) 開始），每次判斷 s[i]==p[j]，為真則 i++,j++，否則，i-=j-1,j=0，繼續匹配，如果 j==m，則匹配成功。但如果一直到 i==n，即退出循環時還未匹配成功，則 \(p\) 不是 \(s\) 的子串

不難證明，暴力法的復雜度為 \(O(nm)\)

KMP模版代碼

考慮優化：我們發現，當 s[i]!=p[j]，即失配時，讓 i-=j-1,j=0的效率過低，而 \(KMP\) 算法則是通過 \(next\) 數組來提高效率，減少無效的匹配

簡略介紹一下，\(next[i]\) 表示以 \(i\) 為結尾的最長公共前后綴，直接給出以下例子：

\(c\) \(z\) \(h\) \(c\) \(z\) \(h\) \(c\) \(z\) \(z\)

\(0\) \(0\) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\) \(0\)

不過多介紹，直接看以下代碼：

luogu P3375 【模板】KMP

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N=1e6+5;
int n,m,nxt[N],f[N];
char s[N],p[N];
void kmp(){
	n=strlen(s+1),m=strlen(p+1);
	int j=0;
	for(int i=2;i<=m;i++){
		while(j&&p[i]!=p[j+1]) j=nxt[j];
		if(p[i]==p[j+1]) j++;
		nxt[i]=j;
	}
	j=0;
	for(int i=1;i<=n;i++){
		while(j==m||j&&s[i]!=p[j+1]) j=nxt[j];
		if(s[i]==p[j+1]) j++;
		f[i]=j;
	}
}
int main(){
	cin>>(s+1)>>(p+1);
	kmp();
	for(int i=1;i<=n;i++) if(f[i]==m) cout<<i-m+1<<endl;
	for(int i=1;i<=m;i++) cout<<nxt[i]<<" ";
	return 0;
}

\(KMP\) 真正重要的是求 \(next\) 數組的思想，以及求出來的 \(next\) 的性質，每道和 \(KMP\) 有關的題，都是和 \(next\) 數組有密切關系的，且性質極其巧妙，需多加練習，這個過程中就會不斷對 \(next\) 數組有更深的了解

CF1029A Many Equal Substrings

一道構造題，先輸出一遍給出的字符串，然后讓指針跳轉回 \(next[n]+1\) ，繼續往后輸出即可，跳轉 \(k-1\) 次

代碼：

#include<bits/stdc++.h>
using namespace std;
const int N=55;
int n,k,nxt[N];
char s[N];
int main(){
	cin>>n>>k>>(s+1);
	int j=0;
	for(int i=2;i<=n;i++){
		while(j&&s[i]!=s[j+1]) j=nxt[j];
		if(s[i]==s[j+1]) j++;
		nxt[i]=j;
	}
	j=1;
	for(int i=1;i<=k;i++){
		while(j<=n) cout<<s[j++];
		j=nxt[n]+1;
	}
	return 0;
}

P4391 [BalticOI 2009] Radio Transmission 無線傳輸

依舊是巧妙的用到了 \(next\) 數組的性質的題，做完這道題，將會對 \(next\) 數組有更深刻的理解。我敢保證，如果你不會，去看題解，一定會直呼 \(WC\)

簡介

題目給出了 \(n（n≤1e6）\) 和長度為 \(n\) 的字符串 \(s\)，已知 \(s\) 是由一個串 \(s1\) 不斷循環構成的，求 \(s1\) 的最小長度（輸入保證 \(s1\) 至少循環了 \(2\) 次）

說說思路：

根據題意，\(s\) 一定由 \(s1\) 至少循環兩次得到，我們給出下圖：

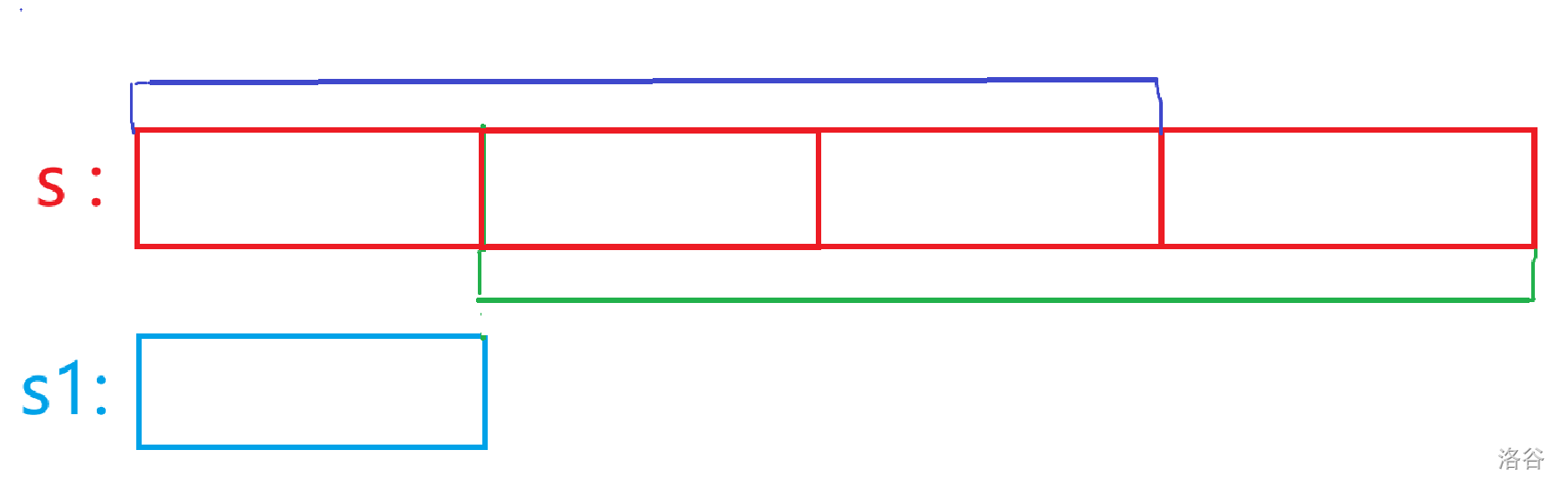
\(s1\) 把 \(s\) 分成了若干段，假設 \(s1\) 就是我們所求的最短串，那么有什么性質？

此時，我們會驚奇的發現：\(next[n]\) 就是代表著了圖中深藍色的前綴和綠色的后綴的長度（最長公共前后綴），藍色部分或者綠色部分加上 \(s1\) 恰好構成完整的 \(s\) ，所以有 \(len(s1)+next[n]=n\)，其中 \(len(s)\) 為要求的 \(s1\) 的長度，\(n\) 為 \(s\) 的長度，那么移項可得：\(len(s1)=n-next[n]\)，所以就完了。

代碼：

#include<bits/stdc++.h>
using namespace std;
const int N=205,L=2e5+5;
int l[N],nxt[N][12],cnt;
string s,p[N];
bool pos[N][L],f[L];
void getnxt(int k){
	int j=0;
	for(int i=2;i<l[k];i++){
		while(j&&p[k][i]!=p[k][j+1]) j=nxt[k][j];
		if(p[k][i]==p[k][j+1]) j++;
		nxt[k][i]=j;
	}
}
void kmp(int k){
	int j=0;
	getnxt(k);
	for(int i=1;i<s.size();i++){
		while((j==l[k])||j&&s[i]!=p[k][j+1]) j=nxt[k][j];
		if(s[i]==p[k][j+1]) j++;
		if(j==l[k]) pos[k][i]=true;
	}
}
int main(){
	string a;
	while(cin>>a){
		if(a==".") break;
		p[++cnt]='.'+a;
		l[cnt]=a.size();
	}
	s=".";
	while(cin>>a) s+=a;
	for(int i=1;i<=cnt;i++) kmp(i);
	f[0]=true;
	for(int i=1;i<s.size();i++){
		for(int j=1;j<=cnt;j++){
			if(pos[j][i]) f[i]|=f[i-l[j]];
		}
	}
	int ans=0;
	for(int i=0;i<s.size();i++) if(f[i]) ans=max(ans,i);
	cout<<ans;
	return 0;
}

P1470 [IOI 1996 / USACO2.3] 最長前綴 Longest Prefix

簡介：

題目給出了一個字符串集合 \(P（元素個數≤200，且最大長度均不超過10）\)，和一個字符串 \(s（len≤2e5）\)，詢問 \(s\) 是否可以只由集合 \(P\) 中的元素構成（不要求 \(P\) 中的所有元素都出現，且可以重復使用 \(P\) 中的元素）

思路：

一道DP題，考慮到 \(P\) 中的元素比較少且長度都很小，我們可以直接讓每個元素都在 \(s\) 上跑一遍 \(KMP\)，把匹配成功的結尾位置標記，然后進行 \(DP\)。

用布爾數組 \(pos[i][j]\) 表示 \(P\) 中第 \(i\) 個元素在 \(s\) 中以 \(s[j]\) 為結尾是否能匹配成功，成功為 \(true\) ，否則為 \(false\)

接著設計 \(DP\)，定義布爾數組 \(f[i]\) 表示以 \(s[i]\) 為結尾的前綴，是否能只由 \(P\) 中的元素構成

轉移方程為：

if(pos[j][i]) f[i]|=f[i-l[j]]; 其中 \(j\) 為枚舉的 \(P\) 中元素的下標

初始化： f[0]=true;

代碼：

#include<bits/stdc++.h>
using namespace std;
const int N=205,L=2e5+5;
int l[N],nxt[N][12],cnt;
string s,p[N];
bool pos[N][L],f[L];
void getnxt(int k){
	int j=0;
	for(int i=2;i<l[k];i++){
		while(j&&p[k][i]!=p[k][j+1]) j=nxt[k][j];
		if(p[k][i]==p[k][j+1]) j++;
		nxt[k][i]=j;
	}
}
void kmp(int k){
	int j=0;
	getnxt(k);
	for(int i=1;i<s.size();i++){
		while((j==l[k])||j&&s[i]!=p[k][j+1]) j=nxt[k][j];
		if(s[i]==p[k][j+1]) j++;
		if(j==l[k]) pos[k][i]=true;
	}
}
int main(){
	string a;
	while(cin>>a){
		if(a==".") break;
		p[++cnt]='.'+a;
		l[cnt]=a.size();
	}
	s=".";
	while(cin>>a) s+=a;
	for(int i=1;i<=cnt;i++) kmp(i);
	f[0]=true;
	for(int i=1;i<s.size();i++){
		for(int j=1;j<=cnt;j++){
			if(pos[j][i]) f[i]|=f[i-l[j]];
		}
	}
	int ans=0;
	for(int i=0;i<s.size();i++) if(f[i]) ans=max(ans,i);
	cout<<ans;
	return 0;
}

目前先寫到這里，之后有空在更新

posted @ 2025-10-18 16:12 czh（抽紙盒）閱讀(8) 評論(0) 收藏舉報

刷新頁面返回頂部

czh-ak-NOI

KMP

KMP

簡介

問題