產(chǎn)生數(shù)

產(chǎn)生數(shù)這道題是一道很好的訓(xùn)練BFS和DFS的題，由于我是一個(gè)萌新，且正在學(xué)習(xí)DFS（深度優(yōu)先搜索），我便把我的DFS代碼展示出來(lái)，以供各位萌新學(xué)習(xí)。如果各位大佬有更好的DFS做法，歡迎向我提出建議。

產(chǎn)生數(shù)

描述

給出一個(gè)整數(shù)n（n≤2000）和k個(gè)變換規(guī)則（k≤15）。規(guī)則：

① 1個(gè)數(shù)字可以變換成另1個(gè)數(shù)字；

② 規(guī)則中，右邊的數(shù)字不能為零。

例如：n=234，k=2規(guī)則為

2 → 5

3 → 6

上面的整數(shù)234經(jīng)過(guò)變換后可能產(chǎn)生出的整數(shù)為（包括原數(shù)）234，534，264，564共4種不同的產(chǎn)生數(shù)。

求經(jīng)過(guò)任意次的變換（0次或多次），能產(chǎn)生出多少個(gè)不同的整數(shù)。僅要求輸出不同整數(shù)個(gè)數(shù)。

輸入

... ...

輸出

輸出滿(mǎn)足條件的整數(shù)個(gè)數(shù)。

輸入樣例 1

輸出樣例1

首先，我們要知道一個(gè)數(shù)學(xué)公式：滿(mǎn)足條件的個(gè)數(shù)之和=（每位數(shù)字的可變化次數(shù)+1）相乘；

如234，1，2->5；則個(gè)位數(shù)字的可變化次數(shù)=0，十位數(shù)字的可變化次數(shù)=0，百位數(shù)字的可變化次數(shù)=1；所以滿(mǎn)足條件的個(gè)數(shù)之和=（0+1）*（0+1）*（1+1）=2；

懂得了這一點(diǎn)，這道題就基本上完成了一半了，然后就是寫(xiě)代碼：

這是我最先的代碼：

這種做法爆了3個(gè)點(diǎn)，經(jīng)過(guò)我思考后，對(duì)代碼進(jìn)行了一些修改，如下：

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 int a[15],b[15],c[4],error[10];
  4 //a,b分別為規(guī)則中x1，y1，c為n的各位數(shù)字，error為統(tǒng)計(jì)重復(fù)出現(xiàn)的數(shù)字
  5 int n,m,tot,tmp,ans=1;
  6 //n為最初的三位數(shù)，m為規(guī)則個(gè)數(shù)，tot統(tǒng)計(jì)每位可變化次數(shù)，tmp用來(lái)統(tǒng)計(jì)無(wú)效位數(shù)，ans用來(lái)記錄答案
  7 //void f(int p)
  8 //{
  9 //    for(int j=0;j<m;j++)//從每個(gè)規(guī)則中尋找符合的
 10 //    {
 11 //        if(p==a[j])
 12 //        {
 13 //            tot++;
 14 //            if(error[p]!=0)//避免無(wú)限調(diào)用f函數(shù)，如果重復(fù)則不調(diào)用
 15 //            {
 16 //                for(int i=0;i<9;i++)
 17 //                {
 18 //                    if(error[i]!=0)
 19 //                    {
 20 //                        tot--;
 21 //                        error[i]=0;//清空數(shù)組
 22 //                    }
 23 //                }
 24 //            }
 25 //            else
 26 //            {
 27 //                error[p]=p;//統(tǒng)計(jì)重復(fù)出現(xiàn)
 28 //                f(b[j]);//遞歸調(diào)用
 29 //            }
 30 //        }
 31 //    }
 32 //}
 33 //void dfs()
 34 //{
 35 //    for(int i=0;i<(4-tmp);i++)
 36 //    {
 37 //        f(c[i]);//調(diào)用f函數(shù)查找某位數(shù)數(shù)字的可變化次數(shù)
 38 //        ans=ans*(tot+1);//滿(mǎn)足條件的個(gè)數(shù)之和
 39 //        tot=0;//清除當(dāng)前位數(shù)的統(tǒng)計(jì)信息，為統(tǒng)計(jì)下一位做鋪墊
 40 //    } 
 41 //}
 42 //int main()
 43 //{
 44 //    cin>>n>>m;//輸入
 45 //    for(int i=0,j=1000;i<4;i++,j/=10)
 46 //    {
 47 //        if(tmp==i&&n/j==0)//統(tǒng)計(jì)無(wú)效位數(shù)
 48 //        {
 49 //            tmp++;
 50 //        }
 51 //        else
 52 //        {
 53 //            c[i-tmp]=n/j%10;//提取各個(gè)位數(shù)上的數(shù)字
 54 //        }
 55 //    }
 56 //    for(int i=0;i<m;i++)
 57 //    {
 58 //        cin>>a[i]>>b[i];//輸入
 59 //    }
 60 //    dfs();//調(diào)用
 61 //    cout<<ans;
 62 //    return 0;
 63 //}
 64 void dfs(int p)
 65 {
 66     error[p] = 1;//打標(biāo)記 
 67     tot++;//相當(dāng)于最后的+1
 68     for(int j = 0; j < m; j++)//從每個(gè)規(guī)則中尋找符合的
 69     {
 70         if(a[j]==p)
 71         {
 72             if(error[b[j]]==0)//避免無(wú)限調(diào)用f函數(shù)，如果重復(fù)則不調(diào)用
 73             {
 74                 f(b[j]);
 75             }
 76         }
 77     }
 78 }
 79 int main()
 80 {
 81     cin>>n>>m;
 82     for(int i=0,j=1000;i<4;i++,j/=10)
 83     {
 84         if(tmp==i&&n/j==0)
 85         {
 86             tmp++;//統(tǒng)計(jì)無(wú)效位數(shù)
 87         }
 88         else
 89         {
 90             c[i-tmp]=n/j%10;//提取各個(gè)位數(shù)上的數(shù)字
 91         }
 92     }
 93     for(int i=0;i<m;i++)
 94     {
 95         cin>>a[i]>>b[i];
 96     }
 97     for(int i=0;i<(4-tmp);i++)
 98     {
 99         dfs(c[i]);
100         ans *= tot;
101         // 當(dāng)前位清理統(tǒng)計(jì)信息，為下一次統(tǒng)計(jì)做準(zhǔn)備 
102         tot=0;
103         for(int j = 0; j <= 9; j++) error[j] = 0;//清空數(shù)組
104     }
105     cout<<ans;
106     return 0;
107 }

這是我老師的做法，思路相同，但寫(xiě)法不一樣：

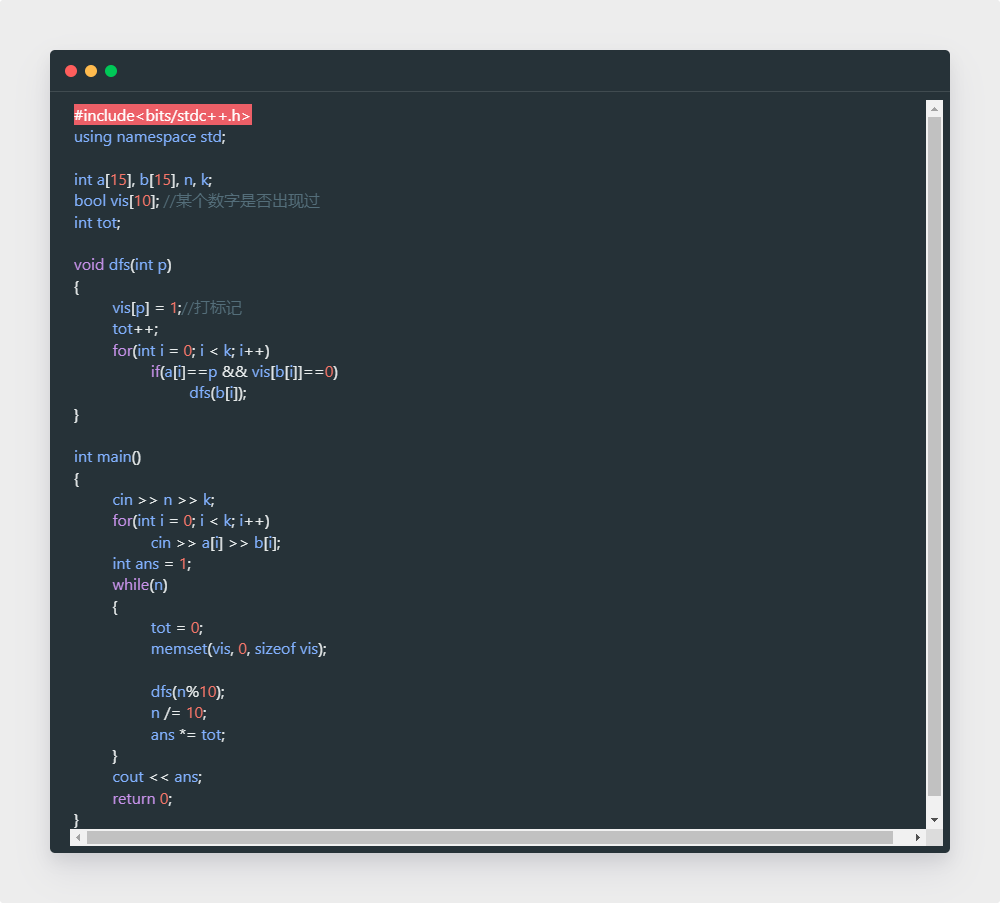
其中作用是把vis數(shù)組清空，作用詳見(jiàn)https://www.csdn.net/gather_27/MtjakgwsNzYtYmxvZwO0O0OO0O0O.html

posted on 2020-02-07 18:31 blcym 閱讀(699) 評(píng)論(0) 收藏舉報(bào)

刷新頁(yè)面返回頂部

公告