成人av午夜在线观看,99久久激情国产精品,成人国产精品中文字幕

斐波那契數列（一）

斐波那契數列（Fibonacci sequence），又稱黃金分割數列，因意大利數學家萊昂納多·斐波那契（Leonardo Fibonacci）以兔子繁殖為例子而引入，故又稱為“兔子數列”。

斐波那契數列指的是這樣一個數列：1，1，2，3，5，8，13，21，34，55，89..，這個數列從第3項開始，每一項都等于前兩項之和。

在數學上，斐波那契數列以如下遞推的方法定義：

F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。

其通項公式為F(n)=

當所求的n值較大時，可以構造一個矩陣，利用矩陣乘法完成斐波那契數列遞推的運算。如下所示。

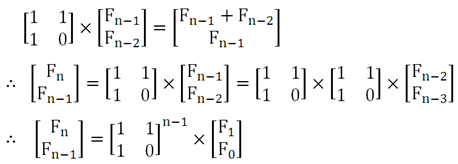
【例1】斐波那契數列

問題描述

斐波那契數列是指這樣的數列：數列的第一個和第二個數都為1，接下來每個數都等于前面2個數之和。

給出一個正整數a，要求菲波那契數列中第a個數是多少。

輸入

每個測試用例由單行中的一個整數n組成，其中0≤n≤50.輸入以-1終止。

輸出

每行輸出對應一個輸入。輸出應是一個正整數，為菲波那契數列中第n個數的大小。

輸入樣例

-1

輸出樣例

（1）編程思路。

由于題目只涉及到斐波那契數列的前50項，因此可以定義一個數組long long f[51]，直接采用遞推的辦法將數列前50項的值求出來并保存。

（2）源程序。

#include <stdio.h>
int main()
{
    long long f[51]={0,1};
    for (int i=2;i<=50;i++)
        f[i]=f[i-1]+f[i-2];
    int n;
    while (scanf("%d",&n) && n!=-1)
    {
        printf("%lld\n",f[n]);
    }
    return 0;
}

將上面的源程序提價給HDU 題庫 HDU 2070 Fibbonacci Number （http://acm.hdu.edu.cn/showproblem.php?pid=2070），可以Accepted。

【例2】還是斐波那契數列

問題描述

大家都知道，斐波那契數列是滿足如下性質的一個數列：

F(n)=1 (n≤2)

F(n)=F(n?1)+F(n?2) (n≥3)

?請你求出 F(n) mod 10⁹ +7 的值。

輸入

一行一個正整數n(1≤n<2⁶³)

輸出

輸出一行一個整數表示答案。

輸入樣例

輸出樣例

（1）編程思路。

由于n值最大可到2⁶³，因此直接用遞推的方式效率太低。構造一個矩陣，采用矩陣快速冪運算進行求解。

（2）源程序。

#include <stdio.h>
#define MODNUM 1000000007
struct Matrix {
      long long s11 , s12 , s21 , s22 ;
};
typedef struct Matrix matrix;
matrix f(matrix a,matrix b)
{
      matrix p ;
      p.s11 = (a.s11*b.s11 + a.s12*b.s21)%MODNUM;
      p.s12 = (a.s11*b.s12 + a.s12*b.s22)%MODNUM;
      p.s21 = (a.s21*b.s11 + a.s22*b.s21)%MODNUM;
      p.s22 = (a.s21*b.s12 + a.s22*b.s22)%MODNUM;
      return p ;
}
matrix quickpow(matrix p,long long n)    // 采用遞歸的方法實現矩陣快速冪運算
{
      matrix q ;
      q.s11 = q.s22 = 1 ;                // 初始化為單位矩陣
      q.s12 = q.s21 = 0 ;
      if (n == 0)
           return q ;
      q = quickpow(p,n/2);
      q = f(q,q);
      if (n%2)
           q = f(q,p);
      return q ;
}
int main()
{
      long long n ;
      matrix p ;
      scanf("%lld", &n);
      p.s11 = p.s12 = p.s21 = 1 ;
      p.s22 = 0 ;
      p = quickpow(p,n);
      printf("%lld\n", p.s12);
      return 0;
}

將上面的源程序提價給洛谷題庫 P1962 斐波那契數列（https://www.luogu.com.cn/problem/P1962），可以Accepted。

【例3】Fibonacci的數字

問題描述

經過一年的努力，數學神童zouyu終于把0到100000000的Fibonacci數列

(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部給背了下來。

接下來，CodeStar決定要考考他，于是每問他一個數字，zouyu就要把答案說出來，不過有的數字太長了。所以規定超過8位的只要說出前4位和后4位就可以了。

輸入

輸入若干數字n(0 <= n <= 100000000)，每個數字一行。讀到文件尾。

輸出

輸出f[n]的前4個數字和后4個數字（若不超過8個數字，就全部輸出）。

輸入樣例

輸出樣例

9227465

63245986

1023...4155

1716...7565

（1）編程思路。

通過輸入輸出樣例可知，當n的值超過39時，斐波那契數列的位數不超過8位。因此先定義一個數組int f[41]，通過遞推的方法直接將n<40時f[n]的值求出并保存，若輸入的n值小于40，直接輸出求得的f[n]值。

當n值較大時，f[n]的位數超過了8位。求后4位比較容易，采用求10000的模即可，使用矩陣快速冪運算來完成，參見上面的例2。

前4位不同于后4位，要考慮進位問題，不能直接取模。將每個f[n]求出來，無論時間復雜度還是空間復雜度都要求太高。

我們知道，斐波那契數列第n項F[n]的通項公式是

將公式兩端取對數可得

其中第三部分非常小，當n很大時趨近于0，可以忽略掉。

再由求得的log₁₀(F[n])求出其高4位。具體方法以f[40]為例說明。

f[40]=102334155

log₁₀(102334155)=log₁₀(1.02334155*10⁸)=log₁₀(1.02334155)+8，

取其小數部分 log₁₀(1.02334155)=0.0100206078，

10^0.0100206078=1.02334155，結果乘以1000取整，即為高4位1023。

（2）源程序。

#include <stdio.h>
#include <math.h>
typedef struct
{
    int s11 , s12 , s21 , s22 ;
}Matrix;
Matrix f(Matrix a,Matrix b)
{
      Matrix p ;
      p.s11 = (a.s11*b.s11 + a.s12*b.s21)%10000;
      p.s12 = (a.s11*b.s12 + a.s12*b.s22)%10000;
      p.s21 = (a.s21*b.s11 + a.s22*b.s21)%10000;
      p.s22 = (a.s21*b.s12 + a.s22*b.s22)%10000;
      return p ;
}
Matrix quickpow(Matrix p,int n)    // 采用遞歸的方法實現矩陣快速冪運算
{
      Matrix q ;
      q.s11 = q.s22 = 1 ;     // 初始化為單位矩陣
      q.s12 = q.s21 = 0 ;
      if (n == 0)
           return q ;
      q = quickpow(p,n/2);
      q = f(q,q);
      if (n%2)
           q = f(q,p);
      return q ;
}
int main()
{
    int f[51]={0,1,1},i;
    for (i=3;i<=40;i++)
    {
        f[i]=f[i-1]+f[i-2];
    }
    int n;
    while (scanf("%d",&n)!=EOF)
    {
        if (n<=39)
            printf("%d\n", f[n]);
        else
        {
            Matrix p ;
            p.s11 = p.s12 = p.s21 = 1 ;
            p.s22 = 0 ;
            p = quickpow(p,n);
            double s = log10(1.0 / sqrt(5.0)) + n * log10((1 + sqrt(5.0)) / 2);
            s -= (int)(s);
            s = pow(10, s);
            while (s < 1000) s *= 10;
            printf("%d...%04d\n", (int)(s),p.s12);
        }
    }
    return 0;
}

將上面的源程序提價給HDU題庫HDU 3117 Fibonacci Numbers （http://acm.hdu.edu.cn/showproblem.php?pid=3117），可以Accepted。

HDU題庫中的 HDU 1568 Fibonacci （http://acm.hdu.edu.cn/showproblem.php?pid=1568）只要求求出f[n]的高4位，將上面的程序進行簡化如下，提交后同樣可以Accepted。

#include <stdio.h>
#include <math.h>
int main()
{
    int f[41]={0,1,1},i,len;
    for (i=3;i<=40;i++)
    {
        f[i]=f[i-1]+f[i-2];
    }
    int n;
    while (scanf("%d",&n)!=EOF)
    {
        if (n<=20)
            printf("%d\n", f[n]);
        else
        {
            double s = log10(1.0 / sqrt(5.0)) + n * log10((1 + sqrt(5.0)) / 2);
            s -= (int)(s);
            s = pow(10, s);
            while (s < 1000) s *= 10;
            printf("%d\n", (int)(s));
        }
    }
    return 0;
}

【例4】有多少個斐波那契數

問題描述

輸入兩個整數a和b，求這兩個數中間有多少個斐波那契數。

輸入

輸入包含幾個測試用例。每個測試用例由兩個非負整數a和b組成。輸入以a=b=0終止。a<=b<=10¹⁰⁰。數字a和b沒有多余的前導零。

輸出

對于每個測試用例，用單獨一行輸出Fibonacci數fi（a<=fi<=b）的數量。

輸入樣例

10 100

1234567890 9876543210

0 0

輸出樣例

（1）編程思路1。

先預先計算一下，斐波那契數列第480項的數字位數將達到100位，因此可以用字符串數組將斐波那契數列中前480項的數計算出來并保存下來。計算時采用高精度加法運算即可。顯然這個字符串數組是按數字升序排列的。對于輸入的字符串a和b，可以通過二分查找得到一個區間[left,right]使得第left個斐波那契數剛好大于a，第right+1個斐波那契數剛好大于b，這樣left~right間斐波那契數的個數就是所求，注意第right個數剛好等于b時需要加1個。

（2）源程序1。

#include <stdio.h>
#include <string.h>
#define MAXLEN    110
#define LAST MAXLEN-2
char fib[481][MAXLEN];    // 存儲480個斐波那契數
void bigNumAdd(char a[],char b[],char c[])
{
     int i,j,n1,n2,n;
     int num1[MAXLEN]={0},num2[MAXLEN]={0};
     // 將a和b中存儲的字符串形式的整數轉換到num1和num2中去，
     // num1[0]對應于個位、num1[1]對應于十位、……
     n1 = strlen(a);
     j = 0;
    for (i = n1 - 1;i >= 0 ; i --)
         num1[j++] = a[i] - '0';
    n2 = strlen(b);
    j = 0;
    for (i = n2 - 1;i >= 0 ; i --)
         num2[j++] = b[i] - '0';
    n=n1>n2?n1:n2;
    for (i = 0;i < n ; i ++ )
    {
         num1[i] += num2[i]; // 逐位相加
         if (num1[i] >= 10 ) // 處理進位
        {
             num1[i] -= 10;
             num1[i+1] ++;
        }
     }
     j=0;
     if (num1[n]!=0) c[j++]=num1[n]+'0';
     for(i=n-1; i>=0; i--)
           c[j++]=num1[i]+'0';
     c[j]='\0';
}
int compare(char *a, char *b)
{
    int lenA = strlen(a);
    int lenB = strlen(b);
     if (lenA == lenB)
    {
        return strcmp(a, b);
    }
    return lenA>lenB ? 1 : -1;
}
int binSearch(char *num, int *flag)
{
    int left,right,mid,res;
    left = 1;
    right= 480;
    while (left <= right)
    {
        mid = (left + right)/2;
        res = compare(num, fib[mid]);
        if (res == 0)
        {
            *flag = 1;
            return mid;
        }
        else if (res < 0)
        {
            right = mid - 1;
        }
        else
        {
            left = mid + 1;
        }
    }
    return left;
}
int main()
{
    int i;
    strcpy(fib[0], "1");
    strcpy(fib[1], "1");
    strcpy(fib[2], "2");
    for (i = 3; i <485; i++)
    {
        bigNumAdd(fib[i-2],fib[i-1],fib[i]);
    }
    char a[MAXLEN], b[MAXLEN];
    while (1)
    {
        scanf("%s%s",a,b);
        if (strcmp(a, "0") == 0 && strcmp(b, "0") == 0)
            break;
        int flagLeft = 0;
        int flagRight = 0;
        //分別找出a和b在斐波那契數中的位置
        //當查找的數不是斐波那契數時，二分查找返回的位置是第一個比它大的斐波那契數的位置
        int left = binSearch(a, &flagLeft);
        int right = binSearch(b, &flagRight);
        //當b也是斐波那契數時，要把兩位置的差值加1
        if  (flagRight)
        {
            printf("%d\n", right - left + 1);
        }
        else
        {
            printf("%d\n", right - left);
        }
    }
    return 0;
}

（3）編程思路2。

上面的源程序1是采用字符串數組來保存各斐波那契數。也可以用整數數組來保存斐波那契數。每個數組元素保留一個斐波那契數中的8位數字。定義一個結構體

struct BigNumber來表示大整數。然后編寫大整數的高精度加法運算程序即可。

（4）源程序2。

#include <stdio.h>
#include <string.h>
#define MOD 100000000
struct BigNumber
{
   int len;
   int num[15];
};
struct BigNumber change(char s[])
{
    struct BigNumber  res;
    memset(res.num,0,sizeof(res.num));
    int i,len=0,k=0,p=1,num=0;
    for (i=strlen(s)-1;i>=0;i--)
    {
        num=num+(s[i]-'0')*p;
        p=p*10;
        k++;
        if (k%8==0)
        {
            res.num[len++]=num;
            num=0;
            p=1;
        }
    }
    if (strlen(s)%8!=0) res.num[len++]=num;
    res.len=len;
    return res;
}
int cmp(struct BigNumber a,struct BigNumber b)  // 比較a,b大小，若a>b返回1，a=b返回0,a<b返回-1
{
    if (a.len!=b.len)
    {
        if (a.len<b.len) return -1;
        else return 1;
    }
    int i;
    for (i=a.len-1;i>=0;i--)
        if (a.num[i]!=b.num[i])
        {
            if (a.num[i]<b.num[i]) return -1;
            else return 1;
        }
    return 0;
}
int main()
{
    struct BigNumber  f[481];
    memset(f[1].num,0,sizeof(f[1].num));
    memset(f[2].num,0,sizeof(f[2].num));
    f[1].len=f[2].len=1;
    f[1].num[0]=1;  f[2].num[0]=2;
    int i,j;
    for (i=3;i<=480;i++)
    {
        memset(f[i].num,0,sizeof(f[i].num));
        f[i].len = f[i-1].len;
        int cf=0;
        for (j=0;j<f[i].len;j++)
        {
           int num=f[i-1].num[j]+f[i-2].num[j]+cf;
           f[i].num[j]=num%MOD;
           cf=num/MOD;
        }
        if (cf!=0)  f[i].num[f[i].len++]=cf;
    }
    char a[105],b[105];
    while (scanf("%s%s",a,b) && (a[0]!='0' || b[0]!='0'))
    {
        struct BigNumber x,y;
        x=change(a);
        y=change(b);
        int left,right,t;
        for (i=1;i<=480;i++)
        {
            t=cmp(x,f[i]);
            if (t<=0)
            {
               left=i-1;
               break;
            }
        }
        for (i=left-1;i<=480;i++)
        {
            t=cmp(y,f[i]);
            if (t!=-1)
                right=i+1;
        }
        printf("%d\n",right-left-1);
    }
    return 0;
}

將上面的兩個源程序分別提交給HDU題庫 HDU 1316 How Many Fibs? （http://acm.hdu.edu.cn/showproblem.php?pid=1316）或北大POJ題庫 POJ 2413 How many Fibs? （http://poj.org/problem?id=2413），均可以Accepted。

【例5】斐波那契的拆分

問題描述

已知任意一個正整數都可以拆分為若干個斐波納契數，現在，讓你求出n的拆分方法。

輸入

一個數t，表示有t組數據

接下來t行，每行一個正整數n（1<=n<=10^9）。

輸出

t行，每行一個字符串，表示拆分方法（格式:n=a1+a2+a3+..+an），要求從小到大輸出。若有多組數據，以個數最小的為準，若仍有多組，輸出右邊盡量大的一組

輸入樣例

輸出樣例

10=2+8

（1）編程思路。

將前45項斐波那契數計算并保存在數組fib中。之后拆分n時，從數組的最后一個元素fib[45]開始試探直到fib[1]，若n大于或等于某個fib[i]，則fib[i]肯定會出現在拆分式中，保存fib[i]，并從n中減去fib[i]。

（2）源程序。

#include <stdio.h>
int main()
{
    int i;
    int fib[46]={0,1,1},a[51];
    for (i=3;i<46;i++)
        fib[i]=fib[i-1]+fib[i-2];
    int t;
    scanf("%d",&t);
    while (t--)
    {
        int n;
        scanf("%d",&n);
        printf("%d=",n);
        int len=0;
        for (i=45;i>=1;i--)
        {
            if (fib[i]<=n && n>=0)
            {
                n-=fib[i];
                a[len++]=fib[i];
            }
        }
        printf("%d",a[len-1]);
        for (i=len-2;i>=0;i--)
        {
            printf("+%d",a[i]);
        }
        printf("\n");
    }
    return 0;
}

將上面的源程序提交給洛谷題庫 P1755 斐波那契的拆分 （https://www.luogu.com.cn/problem/P1755），可以Accepted.

在HDU題庫中下列幾道題目就與斐波那契數列有關，可以作為練習做一做。

【練習1】HDU 1021 Fibonacci Again （http://acm.hdu.edu.cn/showproblem.php?pid=1021）。

#include <stdio.h>
#include <math.h>
int main()
{
    int a[8]={1,2,0,2,2,1,0,1};
    int n;
    while (scanf("%d",&n)!=EOF)
    {
        if (a[n%8]!=0) printf("no\n");
        else printf("yes\n");
    }
    return 0;
}

參考程序

【練習2】HDU 1250 Hat's Fibonacci （http://acm.hdu.edu.cn/showproblem.php?pid=1250）。

#include <stdio.h>
#include <string.h>
#define MOD 100000000
struct BigNumber
{
    int len;
    int a[281];
};
struct BigNumber add(struct BigNumber x,struct BigNumber y)
{
    struct BigNumber z;
    memset(z.a,0,sizeof(z.a));
    z.len=x.len>y.len?x.len:y.len;
    int i,cf=0;
    for (i=0;i<z.len;i++)
    {
        z.a[i]=x.a[i]+y.a[i]+cf;
        cf=z.a[i]/MOD;
        z.a[i]=z.a[i]%MOD;
    }
    if (cf!=0) z.a[z.len++]=cf;
    return z;
}
void print(struct BigNumber x)
{
    int i;
    printf("%d",x.a[x.len-1]);
    for (i=x.len-2;i>=0;i--)
        printf("%08d",x.a[i]);
    printf("\n");
}
struct BigNumber f[7505]={0};
int main()
{
    struct BigNumber t;
    memset(f[1].a,0,sizeof(f[1].a));
    memset(f[2].a,0,sizeof(f[2].a));
    memset(f[3].a,0,sizeof(f[3].a));
    memset(f[4].a,0,sizeof(f[4].a));
    f[1].len=f[1].a[0]=1;
    f[2].len=f[2].a[0]=1;
    f[3].len=f[3].a[0]=1;
    f[4].len=f[4].a[0]=1;
    int i;
    for (i=5;i<=7500;i++)
    {
        t=add(f[i-4],f[i-3]);
        t=add(t,f[i-2]);
        t=add(t,f[i-1]);
        f[i]=t;
    }
    int n;
    while (scanf("%d",&n)!=EOF)
    {
        print(f[n]);
    }
    return 0;
}

參考程序

【練習3】HDU 1708 Fibonacci String （http://acm.hdu.edu.cn/showproblem.php?pid=1708）。

#include <stdio.h>
#include <string.h>
int main()
{
    int t;
    scanf("%d",&t);
    while (t--)
    {
        long long a1[27],a2[27],temp[27];
        memset(a1,0,sizeof(a1));
        memset(a2,0,sizeof(a2));
        char s0[31],s1[31];
        int n;
        scanf("%s%s%d",s0,s1,&n);
        int i,j;
        for (i=0;s0[i]!='\0';i++)
           a1[s0[i]-'a']++;
        for (i=0;s1[i]!='\0';i++)
           a2[s1[i]-'a']++;
        for (i=2;i<=n;i++)
        {
           for (j=0;j<26;j++)
           {
              temp[j]=a2[j];
              a2[j]+=a1[j];
              a1[j]=temp[j];
           }
        }
        if(n==0)
        {
            for (i=0;i<26;i++)
              a2[i]=a1[i];
        }
        for(i=0;i<26;i++)
        {
            printf("%c:%lld\n",i+'a',a2[i]);
        }
        printf("\n");
    }
    return 0;
}

參考程序

【練習4】HDU 3306 Another kind of Fibonacci （http://acm.hdu.edu.cn/showproblem.php?pid=3306）。

#include <stdio.h>
#include <string.h>
#define MOD 10007
struct Matrix
{
    int mat[5][5];   // 存儲矩陣中各元素
};
Matrix matMul(Matrix a ,Matrix b,int n)
{
    Matrix c;
    memset(c.mat,0,sizeof(c.mat));
    int i,j,k;
    for (k = 1; k<=n ; k++)
      for (i=1 ;i<=n ; i++)
         if (a.mat[i][k]!=0)
            for (j = 1 ;j<=n ;j++)
               c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % MOD;
    return c;
}
Matrix quickMatPow(Matrix a ,int n,int b) // n階矩陣a快速b次冪
{
    Matrix c;
    memset(c.mat ,0 ,sizeof(c.mat));
    int i;
    for (i = 1 ;i <= n ;i++)
        c.mat[i][i] = 1;
    while (b!=0)
    {
        if (b & 1) 
            c = matMul(c ,a ,n);    // c=c*a;   
        a = matMul(a ,a ,n);        // a=a*a
        b /= 2;
    }
    return c;
}
int main()
{
    int n,x,y,ans;
    Matrix p;
    while(scanf("%d%d%d" ,&n ,&x ,&y)!=EOF)
    {
        x = x%MOD;
        y = y%MOD ;
        if (n==2)
             printf("%d\n" ,(x*x%MOD+y*y%MOD+2*x*y%MOD+2)%MOD) ;
        else
        {
           memset(p.mat,0,sizeof(p.mat));
           p.mat[1][1]=p.mat[3][2]=1;   
           p.mat[1][2]=p.mat[2][2]=(x*x)%MOD;
           p.mat[1][3]=p.mat[2][3]=(y*y)%MOD;
           p.mat[1][4]=p.mat[2][4]=(2*x*y)%MOD;
           p.mat[4][2]=x;
           p.mat[4][4]=y;
           p = quickMatPow(p,4,n-1);
           ans=(p.mat[1][1]*2%MOD+p.mat[1][2]+p.mat[1][3]+p.mat[1][4])%MOD;
           printf("%d\n" ,ans);
        }
    }
    return 0; 
}

參考程序

【練習5】HDU 6462人類史上最大最好的希望事件（http://acm.hdu.edu.cn/showproblem.php?pid=6462）。

// a+b代表轉了a個完整的圈加上b個1/4圈。求a+b轉到b+c劃過的面積差。
#include <stdio.h>
#define MOD 192600817
int main()
{
    long long fib[40005],sum[40005];
    fib[1] = fib[2] =1;
    sum[1] = 1;
    sum[2] = 2;
    int i;
    for (i=3;i<40005;i++)
    {
        fib[i] = (fib[i-1]+fib[i-2])%MOD;
        sum[i] = (sum[i-1] + fib[i]*fib[i]%MOD)%MOD;
    }
    int t;
    while (~scanf("%d",&t))
    {
        while (t--)
        {
            int a,b,c,d,tmp;
            scanf("%d %d %d %d",&a,&b,&c,&d);
            int st = a*4+b;
            int ed = c*4+d;
            if (ed < st) { tmp=st; st=ed; ed=tmp; }
            printf("%lld\n",(sum[ed+1]-sum[st]+MOD)%MOD);
        }
    }
    return 0;
}

參考程序

【練習6】HDU 5018 Revenge of Fibonacci （http://acm.hdu.edu.cn/showproblem.php?pid=5018）。

#include <stdio.h>
int main()
{
    int t;
    scanf("%d",&t);
    while (t--)
    {
        long long a,b,c,x;
        scanf("%lld%lld%lld",&a,&b,&x);
        if (x==a || x==b)
        {
            printf("Yes\n");
            continue;
        }
        while (1)
        {
            c=a+b;
            if (c>=x) break;
            a=b;  b=c;
        }
        if (c==x) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

參考程序

posted on 2022-12-15 07:24 aTeacher 閱讀(3514) 評論(0) 收藏舉報

刷新頁面返回頂部

I am a teacher!

導航

公告

斐波那契數列（一）