這一篇博文想寫很久了，一直沒有下筆，核心原因也是有一些待辦的思路在攻關驗證。

我們先從一個核心的問題出發，

1. 為什么要研究優化器算法？

它的關聯問題：訓練為什么要調參，調的是什么參？

如果就這個問題去問各種大語言模型，它們能給出一堆的理由。

但就博主而言，答案只有一個：

干掉調參，解放生產力，榨干算力。

說到底就一個字"窮"。

在多年的研發生涯里，對調參這個事深惡痛絕，為什么辛辛苦苦架構出來的模型，一訓練就崩，訓練收斂慢到龜速，這嚴重影響了開發進度，并且增加了很多不可抗力的消耗。

我相信有很多業內同行，都有這種痛，訓練了很久，效果依舊很差，泛化能力也不行，然后就開始苦惱，為什么自己沒有足夠的錢，足夠的算力。

明明自己很好的思路，戛然而止，退而求其次。

早年間，博主經常半夜醒來，看訓練的損失曲線，生怕訓崩。就算沒有訓崩，自己花費了大量時間精力，卻沒有很好的回報。

一次又一次，是很打擊信心的。

在付出了大量時間和人民幣之后，博主終于從泥潭里爬出來了，時光荏苒，這個困擾我九年的問題，畫上句號了。

那大語言模型是怎么回答這個問題的。

核心就一句話：

"沒有新優化器，下一代模型根本訓不起來。"

• 從理論上看，它是在解決一個尚未被完全理解的復雜高維優化問題，充滿挑戰與機遇。

  解決基礎性訓練難題——讓模型"能學"

• 從工程上看，它是降低AI研發成本、推動技術普及的關鍵杠桿。

  追求極致的效率與效益——讓模型"快學"且"省學"

• 從性能上看，它是提升模型最終準確性、魯棒性和泛化能力的決定性因素。

  提升模型的終極性能——讓模型"學好"

最終達到，拓展AI的技術邊界——讓"不可能"成為"可能"

當然就這個問題，大家可以自行去追問各家的大語言模型，給出的結論大同小異。

2. 那博主為什么要寫這篇博文？

最基本的還是希望拋磚引玉，希望能有更多的同行在力大磚飛，燒錢的當下，不要放棄底層算法的研究。

同時為更多的深度學習小白提供一個新的視角，學習并應用深度學習，溫故而知新。

3. 那什么是優化器算法？

優化器算法是驅動機器學習模型學習的"引擎"。它的核心任務是：在訓練過程中，根據損失函數計算出的梯度（即方向），以某種策略更新模型的參數，從而最小化損失函數。

可以將訓練過程想象成在復雜地形中尋找最低點：

• 損失函數：代表地形的高度。
• 模型參數：代表我們在地形中的位置。
• 梯度：代表我們腳下最陡峭的下坡方向。
• 優化器：就是那個決定"往哪個方向走、走多大步、以及是否要考慮之前的慣性"的導航策略。

Adam (Adaptive Moment Estimation)

• 思想：目前最流行和默認的優化器之一。它結合了Momentum和RMSProp的優點。

  • 它計算梯度的一階矩（均值，提供動量）和二階矩（未中心化的方差，用于自適應調整學習率）。
  • 然后對這兩個矩進行偏差校正，使其在訓練初期不那么偏向于0。

• 優點：

  • 通常收斂速度快。
  • 對超參數的選擇相對魯棒（默認參數通常就能工作得很好）。
  • 能處理噪聲和稀疏梯度。

如果把Adam的一階矩和二階矩去掉，它就蛻變為SGD。

而隨機梯度下降(樸素SGD)是一種優化算法，通過隨機選取單個樣本來近似梯度，從而迭代更新模型參數，收斂至最小值。

換句話說，樸素SGD是一個沒有應用任何先驗補充的野蠻人，較于Adam的平滑學習而言，它就像一只無頭蒼蠅，到處亂撞，也不知道該撞多少次才能收斂至最小值。

4. Adam相較于樸素SGD，它做了哪些改進？

• 引入動量緩沖m，也就是一階矩，指數加權平滑梯度，它積累了歷史梯度的方向趨勢。使得樸素SGD的動蕩趨于平穩平滑。

• 引入自適應步長v，也就是二階矩，指數加權平均的平方，它積累了歷史梯度平方的值趨勢。

最終以 grad = m / sqrt(v) 作為目標梯度進行更新。

對于動量一階矩，基本沒啥好說的，就是求歷史平均梯度，使得訓練平穩。

核心還是自適應步長v，對于頻繁更新、梯度大的參數，其二階矩估計值大，因此實際更新步長會被調小（除以一個大數），避免"步子太大"而越過最優點。

對于不頻繁更新、梯度小的參數，則給予更大的相對步長，鼓勵其更新。

所以Adam能加速較于樸素SGD訓練收斂，二階矩功不可沒。

原本故事到這里，就接近完結了。

在真實的場景下，我們發現Adam還是不夠好。

但它的普及使得深度學習遍地開花。

雖然仍是需要調參，但是不像之前那么"玄學"了。

當然在一些場景下，例如GAN的訓練，仍然有所爭議。

Adam is no better than normalized SGD: Dissecting how adaptivity improves GAN performance | OpenReview

在博主的實測下，此文提及的nSGDA確實比樸素SGD穩健一些。

class nSGDA(torch.optim.Optimizer):
    def __init__(
            self,
            params,  # Model parameters
            lr: Union[float, torch.Tensor] = 4e-5,  # Learning rate (default: 4e-5)
            # Coefficients used for computing running averages of gradient (default: 0.9)
            momentum: float = 0.9,
            # eps (float, optional): term added to the denominator to improve numerical stability (default: 1e-8)
            eps: float = 1e-8,
            weight_decay: float = 1e-2,  # Weight decay (L2 penalty) (default:1e-2)
    ):
        if lr < 0.0:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if not 0.0 <= eps:
            raise ValueError("Invalid epsilon value: {}".format(eps))
        if momentum < 0.0 or momentum >= 1.0:
            raise ValueError("Invalid momentum value: {}".format(momentum))
        if weight_decay < 0.0:
            raise ValueError("Invalid weight decay: {}".format(weight_decay))
        defaults = dict(
            lr=lr,
            momentum=momentum,
            weight_decay=weight_decay,
            eps=eps)
        super().__init__(params, defaults)

    def step(self, closure=None):
        r"""Performs a single optimization step.

        Arguments:
            closure: A closure that reevaluates the model and returns the loss.
        """
        loss = None
        if closure is not None:
            loss = closure()
        for group in self.param_groups:
            momentum = group['momentum']
            lr = group['lr']
            weight_decay = group['weight_decay']
            eps = group['eps']
            one_minus_momentum = 1.0 - momentum
            for p in group['params']:
                if p.grad is None:
                    continue
                if p.grad.is_sparse:
                    raise RuntimeError(
                        "current optimizer does not support sparse gradients")
                state = self.state[p]
                # State initialization
                if len(state) == 0:
                    state["m"] = torch.zeros_like(p.grad, memory_format=torch.preserve_format)
                m = state['m']
                bias_correction = 1.0 - momentum ** state["step"]
                if weight_decay != 0:
                    p.grad = p.grad.add(p.data, alpha=weight_decay)
                m.mul_(momentum).add_(p.grad, alpha=one_minus_momentum)
                step_size = lr / torch.norm(m.div(bias_correction)).add_(eps).mul_(bias_correction)
                p.data.add_(m, alpha=-step_size)
        return loss

當你采用Adam調參訓練，總是跑崩或者無法收斂，這個時候，稍微嘗試一下nSGDA也未嘗不可。

而Adam二階矩的存在也實實在在埋了一個雷 : “過沖”問題

本來“對于不頻繁更新、梯度小的參數，則給予更大的相對步長，鼓勵其更新。”

是個很好的想法，

但是有一個特例，那就是訓練到后期，梯度理論上也會越來越小，這個時候也不應該鼓勵其更新。

有可能一更新，跑飛了，這就是后來為什么存在早停（Early Stopping）策略的根由之一。

如果繼續訓練，有可能從次優解里爬出來，但是更多實際情況是，若這里就是最優解，

由于激進地更新，反而會越跑越遠。

理想的情況肯定是，訓練到最優解。最后停在最優解上，或者在最優解周圍轉圈。

但這里有個悖論，

你憑什么認為這里是最優解，而不是次優解，這個標準怎么界定判斷。

而且由于數據的稀缺性，我們希望模型在這種情況下，還能有更強大的泛化能力，即使它沒見過的數據，也能適配到位。

也就是說，

理想上我們既希望能求到解的思路規律，最好覆蓋更多的求解路徑，而不是一條最短的求解路徑。

繞路沒問題，只要這個繞路方式能提升泛化能力。

[1207.0580v1] Improving neural networks by preventing co-adaptation of feature detectors

這就是后來dropout盛行的原因之一，因為簡單有效。

讓一部分神經元失活，也能求到解。

但是dropout這個技術思路，慎用，用得不好，反而會起反作用。

路漫漫其修遠兮，一起努力吧～

5. 后Adam家族時代，百家爭鳴

由于這個話題展開，真的可以寫一本書了。

所以本文的核心是"速覽"，博主帶著大家看一看這后Adam的各種巧思。

相關的算法實現，可以參考以下項目倉庫：

PyTorch:
https://github.com/kozistr/pytorch_optimizer

TensorFlow/Keras:
https://github.com/NoteDance/optimizers

本文沒有提及的其他算法，自行移步查閱。

5.1 砍Adam的顯存

由于一階矩m和二階矩v都需要歷史平滑，所以Adam至少要占用兩倍的可訓練模型參數。

這樣一來，只要模型參數一大，那訓練的時候 1+2 = 3 至少要存儲三份權重。顯存很快就不夠用了。

所以，針對這個問題，我們開始磨刀霍霍向二階矩v。

5.1.1 18年的Adafactor

[1804.04235v1] Adafactor: Adaptive Learning Rates with Sublinear Memory Cost

社區比較知名的實現：

transformers/src/transformers/optimization.py at main · huggingface/transformers · GitHub

5.1.2 19年的SM3

[1901.11150] Memory-Efficient Adaptive Optimization

官方實現：
https://github.com/google-research/google-research/tree/master/sm3

Adafactor和SM3都是分解近似的做法。SM3的實現較為復雜，所以基本上沒有被推廣開來。所以很長一段時間都是Adafactor是主流。

但是Adafactor的實現稍微有些問題。

問題函數：

@staticmethod
def _approx_sq_grad(exp_avg_sq_row, exp_avg_sq_col):
    # copy from fairseq's adafactor implementation:
    # https://github.com/huggingface/transformers/blob/8395f14de6068012787d83989c3627c3df6a252b/src/transformers/optimization.py#L505
    r_factor = (exp_avg_sq_row / exp_avg_sq_row.mean(dim=-1, keepdim=True)).rsqrt_().unsqueeze(-1)
    c_factor = exp_avg_sq_col.unsqueeze(-2).rsqrt()
    return torch.mul(r_factor, c_factor)

_approx_sq_grad 這個實現丟失了不少精度。

博主認為比較合理的實現，是把sqrt放到最后計算，精度會高些。

@staticmethod
def _approx_sq_grad(row_exp_avg_sq, col_exp_avg_sq):
    row_factor = row_exp_avg_sq.unsqueeze(-1)
    row_factor = row_factor.mean(dim=-2, keepdim=True).div(row_factor)
    col_factor = col_exp_avg_sq.unsqueeze(-2)
    return row_factor.div(col_factor).sqrt_()

5.1.3 22年的Amos

[2210.11693]Amos: An Adam-style Optimizer with Adaptive Weight Decay towards Model-Oriented Scale

在Adafactor和SM3之后很長一段時間，砍優化器顯存占用這個事情似乎被遺忘了。

直到Amos的出現，它進一步砍掉了v的顯存占用，直接采用了平方均值，美其名曰"信息共享"。

顯存不夠用，又想保住精度，可以考慮采用Amos，當然它較之Adam還有不少改進點。

5.1.4 24年損失作為學習率的奇思妙想

利用損失值（loss）本身來動態調整優化器的學習率，以此作為替代二階v實現更快的收斂。

非常簡單的思路: “損失越大，學習率越大；損失越小，學習率越小。”

AdaLo: Adaptive learning rate optimizer with loss for classification

由于論文沒有給出開源實現，也沒有搜到第三方實現。

參考論文的思想，實現了該思路，代碼實現不完全對應論文內容，僅供參考學習。

# mypy: allow-untyped-defs
from typing import Tuple, Union

import torch
from torch import GradScaler


class AdaLo(torch.optim.Optimizer):
    r"""
       AdaLo: Adaptive Learning Rate Optimizer with Loss for Classification
       paper: https://www.sciencedirect.com/science/article/abs/pii/S0020025524015214
       code:  https://github.com/cpuimage/AdaLo

       usage:
           for inputs, labels in dataloader:
               def closure(inp=inputs, lbl=labels):
                   optimizer.zero_grad()
                   loss = criterion(model(inp), lbl)
                   loss.backward()
                   return loss
               optimizer.step(closure)

       Args:
           params: Iterable of parameters to optimize or dicts defining
            parameter groups.
           lr: Learning rate (not used for step size calculation due to the adaptive learning rate mechanism; retained solely for API consistency)
           betas: (beta1, beta2) coefficients for gradient momentum and loss-EMA smoothing respectively
           weight_decay: L2 weight decay
           kappa: loss scaling factor
           eps: float. term added to the denominator to improve numerical stability.
           mode: control learning rate adaptation mode ('adversarial' or 'compliant')
                 'adversarial': decrease learning rate when loss increases (conservative strategy)
                 'compliant': increase learning rate when loss increases (aggressive strategy)
       """

    def __init__(self,
                 params,
                 lr: Union[float, torch.Tensor] = 1e-8,
                 betas: Tuple[float, float] = (0.9, 0.999),
                 weight_decay: float = 1e-2,
                 kappa: float = 3.0,
                 eps: float = 1e-8,
                 mode: str = 'adversarial'):
        if lr < 0.0:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if betas[0] < 0.0 or betas[0] >= 1.0:
            raise ValueError("Invalid beta1 value: {}".format(betas[0]))
        if betas[1] < 0.0 or betas[1] >= 1.0:
            raise ValueError("Invalid beta2 value: {}".format(betas[1]))
        if weight_decay < 0.0:
            raise ValueError("Invalid weight decay: {}".format(weight_decay))
        defaults = dict(lr=lr, beta1=betas[0], beta2=betas[1], weight_decay=weight_decay, kappa=kappa,
                        mode=mode, eps=eps)
        super(AdaLo, self).__init__(params, defaults)

    def step(self, closure=None, scaler: GradScaler = None, loss=None):
        already_updated_by_scaler = False
        if closure is not None:
            with torch.enable_grad():
                loss = closure()
            if scaler is not None:
                scaler.scale(loss).backward()
                scaler.unscale_(self)
                scaler.step(self, loss=loss)
                scaler.update()
                already_updated_by_scaler = True
        if not already_updated_by_scaler:
            for group in self.param_groups:
                beta1 = group['beta1']
                beta2 = group['beta2']
                weight_decay = group['weight_decay']
                kappa = group['kappa']
                mode = group['mode']
                eps = group['eps']
                for p in group['params']:
                    if p.grad is None:
                        continue
                    if p.grad.is_sparse:
                        raise RuntimeError("current optimizer does not support sparse gradients")
                    state = self.state[p]
                    if len(state) == 0:
                        state['m'] = torch.zeros_like(p.data)
                        state['loss_ema'] = torch.tensor(0.0, device=p.device, dtype=p.dtype)
                    m = state['m']
                    loss_ema = state['loss_ema']
                    m.lerp_(p.grad, 1.0 - beta1)
                    if loss is not None:
                        scaled_loss = torch.log1p(loss.detach())
                        transformed_loss = (torch.tanh(-scaled_loss * 0.5) + 1.0) * 0.5
                        loss_ema.lerp_(transformed_loss, 1.0 - beta2)
                    if mode == 'adversarial':
                        lr_t = loss_ema.div(kappa).clamp_min_(eps)
                    else:
                        lr_t = (1.0 - loss_ema).div(kappa).clamp_min_(eps)
                    if weight_decay != 0:
                        p.data.mul_(1.0 - lr_t * weight_decay)
                    p.data.sub_(m * lr_t)
        return loss

在一些場景下實測也是很穩健，lr = v = loss 不得不夸一下論文原作者的奇思妙想。

PyTorch官方使用amp混合精度的時候，GradScaler.step里有這么一句。

if "closure" in kwargs:
    raise RuntimeError(
        "Closure use is not currently supported if GradScaler is enabled."
    )

也就是說閉包和amp混合當前不支持一起用。

在AdaLo代碼倉庫里，博主演示怎么魔改實現閉包和amp可以同時使用，感興趣的可以閱讀具體實現。

在實測過程中，發現 “損失越大，學習率越大；損失越小，學習率越小。” 

這個做法在一些場景下比較激進，所以增加了一個新的參數為mode可切換學習率適配模式，默認設為保守模式。

分別對應

- adversarial (保守模式)：“損失越大，學習率越小；損失越小，學習率越大。” 
- compliant (激進模式) ：“損失越大，學習率越大；損失越小，學習率越小。”

5.1.5 窮到極致，什么都能接受

如果顯存極度匱乏，手頭還挺緊，能訓練比什么都重要的話。

[2412.08894] SMMF: Square-Matricized Momentum Factorization for Memory-Efficient Optimization

采用 非負矩陣分解(NNMF)，將梯度權重轉換為最接近正方形的矩陣，分解為行列兩個向量。

雖然是有損的壓縮解壓操作，但在一些特定的場景能減少可觀的內存占用，在內存效率和優化性能之間取得相對平衡。

核心算法如下:

  @torch.no_grad()
    def _unnmf(self, row_col: tuple) -> torch.Tensor:
        return torch.outer(row_col[0], row_col[1])

    @torch.no_grad()
    def _nnmf(self, matrix: torch.Tensor, out) -> tuple:
        shape = matrix.shape
        torch.sum(matrix, dim=1, out=out[0])
        torch.sum(matrix, dim=0, out=out[1])

        if shape[0] < shape[1]:
            scale = out[0].sum()
            if scale != 0:
                torch.div(out[0], scale, out=out[0])
        else:
            scale = out[1].sum()
            if scale != 0:
                torch.div(out[1], scale, out=out[1])

        return out

5.2 Adam二階矩v為0的問題

導致v為0有很多原因，在模型訓練的不同階段，由于噪聲也好，精度也好，會直接或者間接導致v為0。

前面提到 grad = m / sqrt(v)

早期Adam論文里的解決方案就是直接給v加上一個epsilon，一般設為1e-8，避免除以0。

而后續經過不少團隊的實踐發現這么做有點魯莽。

然后就有人開始針對這個問題進行修改。

但是林林總總，都是把epsilon移來移去，例如梯度平方后就加上epsilon，再進行指數加權平均。

也有采用softplus抑制分母過小的做法:

[1908.00700] Calibrating the Adaptive Learning Rate to Improve Convergence of ADAM

 grad = m / softplus(sqrt(v))


這個問題一直到了2024年，有新的進展。

[2407.05872v2] Scaling Exponents Across Parameterizations and Optimizers

方法很簡單，刪除epsilon，采用atan2。

grad = atan2(m, sqrt(v))

從數值穩定的角度來說，atan2確實是穩定了許多，而且基本規避了一些特殊情況下訓練跑崩，導致損失為nan的情況。

Adam的betas默認參數是(0.9,0.999) ,也有人覺得這里也存在調參適配問題。

刪除epsilon一般都可以理解，但把動量參數也干掉，做成自適應的"膽大妄為"，也是挺絕的。

[2510.04988v1] Adaptive Memory Momentum via a Model-Based Framework for Deep Learning Optimization

不管成不成功，效果幾何，就這魄力，值得我在此一提。

5.3 Adam的梯度長尾問題

這個很好理解，由于一階矩m和二階矩v都采用了指數平均，在不同程度上也是導致梯度長尾的誘因之一。

因為求平均值這個事，就跟奧運比賽打分一樣，只用均值很不公平。去掉一個最高分，去掉一個最低分，然后再算平均相對合理一些。

求損失均值的時候一樣存在，博主曾經設想過，也許求損失的中位數是一個可行的做法，但也有一定的局限性。

沒有經過嚴格驗證的求損失中位數思路的實現，僅供參考：

def soft_median(losses, temperature=None):
    if temperature is None:
        temperature = max(0.1, 0.5 * losses.std())
    if losses.numel() % 2 == 0:
        losses = torch.cat([losses, losses.new_zeros(1)])
    x_sorted, _ = torch.sort(losses)
    n_loss = losses.shape[0]
    median_idx = (n_loss - 1) * 0.5
    idxs = torch.arange(n_loss, device=losses.device, dtype=losses.dtype)
    weights = torch.softmax(-torch.abs(idxs - median_idx) / temperature, dim=0)
    return torch.dot(weights, x_sorted)

同樣的，梯度在訓練過程中變化很大，一些長尾樣本帶來的貢獻就會被淹沒掉。

帶來的后果，不是過擬合，就是泛化差，能拿到次優解那是屬于幸運兒了。

這個方向的研究多，也不多，因為很多長尾問題基本上不會考慮在優化器里解決，一般會采用損失加權懲罰的思路來緩解。

這篇論文可以幫助進一步理解梯度長尾問題。

[2201.05938v2] GradTail: Learning Long-Tailed Data Using Gradient-based Sample Weighting

當然它不是一個主流的方案和思路，主流的方案更多的是采用元學習之類的做法，局限性也比較大。

那該如何直觀地洞察梯度長尾呢？

采用TensorBoard，對參數和梯度進行可視化，查看其直方圖，非常直觀。

示例如下:

參數直方圖:

從參數權重的分布來看，藍色左邊一直在拖尾，紅色的左邊尾巴開始右移聚攏。從參數來看，可以看到一些趨勢，但不夠直觀。

我們再來看其對應的梯度直方圖:

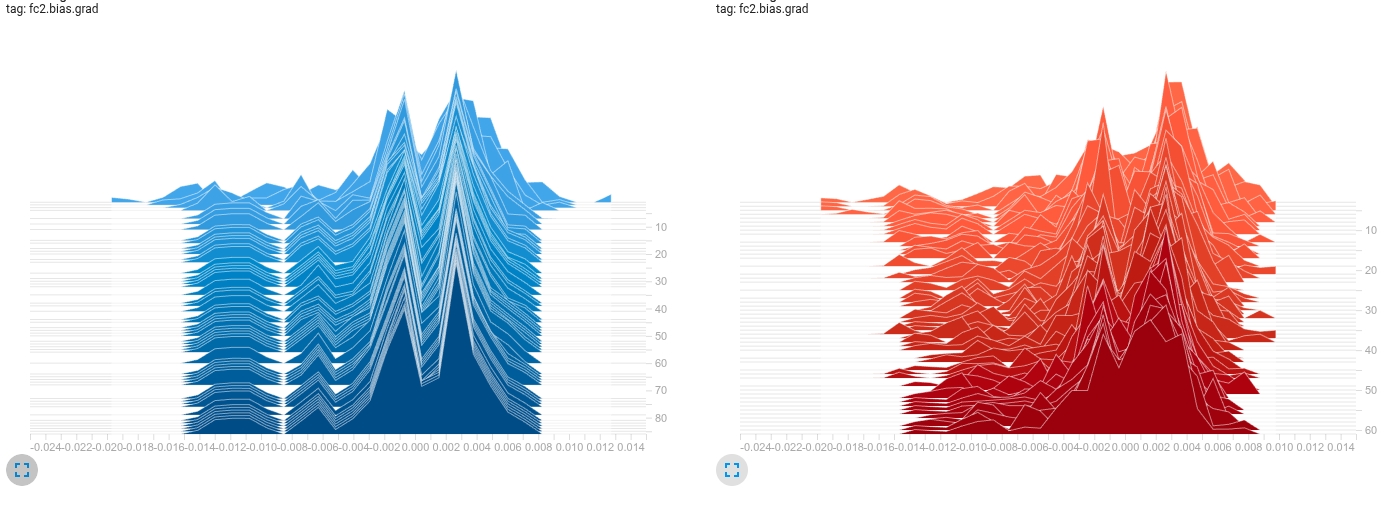
這就一目了然，左邊藍色明顯存在梯度長尾，而右邊紅色的梯度長尾逐漸開始消失，且紅色更趨向于正態分布。

我們再看另一組圖:

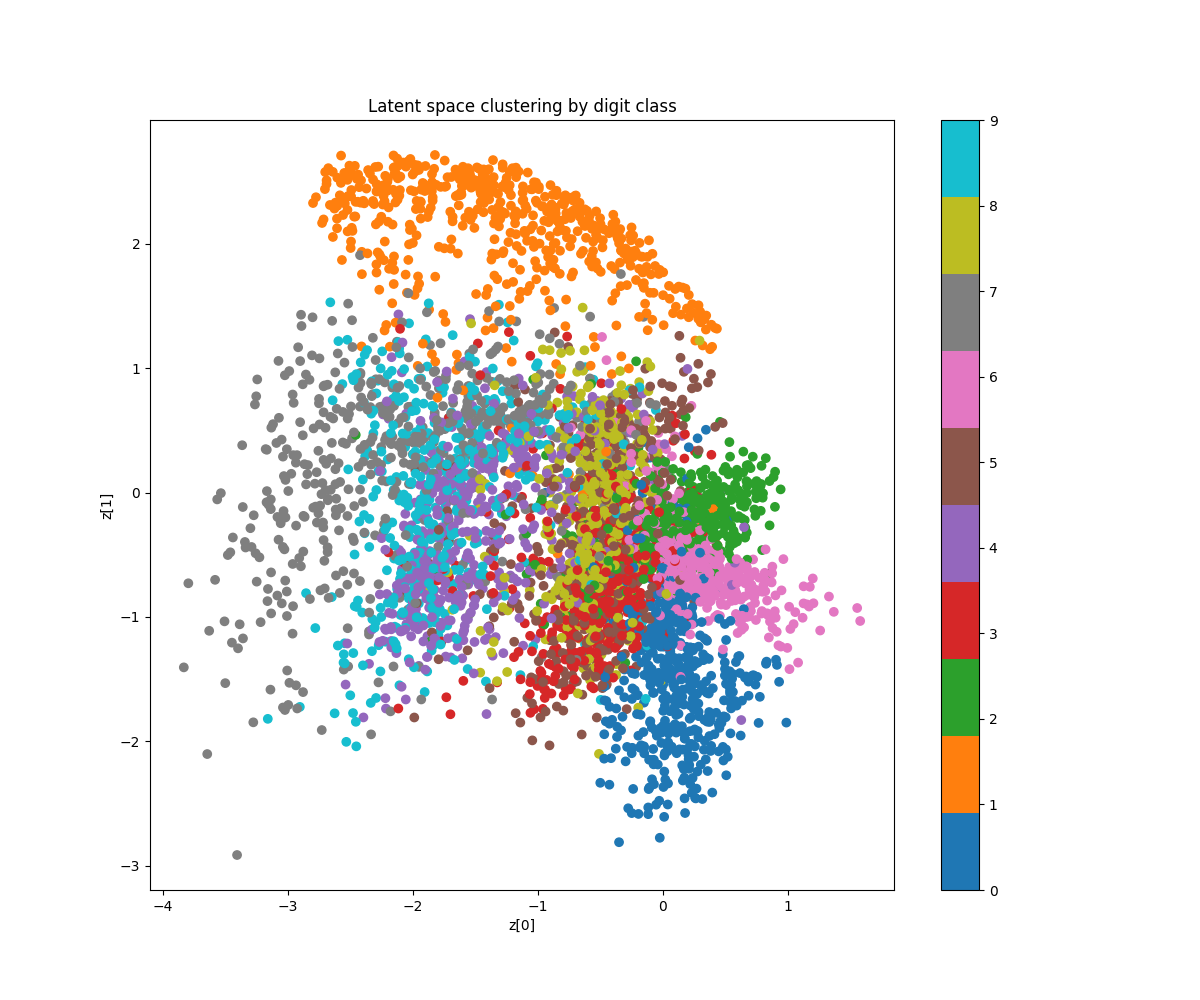
這是vae潛空間0-9十個數字的聚類圖。

相關vae代碼示例見：https://github.com/cpuimage/AdaLo

圖二整體聚合接近一個圓圈，而圖一接近橢圓。

這兩種情況，是圖二還是圖一的模型權重泛化能力更勝一籌呢。

答案是圖二，它的kl散度損失更低。

真實情境下長尾也可以是噪聲或標簽錯誤，所以擬合長尾也不是完全是一件好事情。

一切以實測效果為準，長尾梯度只是一個僅供參考項。

博主一直認為如果可以優雅解決長尾問題，那是新一輪的曙光。

5.4 Adam的過擬合問題

由于Adam本身的機制問題，

訓練損失下降極快 → 模型迅速進入插值（interpolation）區域 → 參數范數容易膨脹 → 邊界更復雜 → 泛化差。

當然長尾問題也是它導致過擬合的原因之一。

比較知名且使用廣泛的方案是l2正則化，即權重衰減。

Adam 進化為 AdamW，也就是現在主流的優化器算法

它思路也是非常簡單粗暴，在每次更新時，從權重中減去一個固定的比例（weight * weight_decay），是正則也是先驗懲罰。

[1711.05101v3] Decoupled Weight Decay Regularization

權重衰減是一個很好的思路，但它帶來了一個新的問題。衰減量設為多少才是合適的，也就是說，懲罰力度該如何界定。

衰減過大，學習收斂緩慢，衰減過小，沒有起到作用。

隨后Scheduled (Stable) Weight Decay也被提出，但是應用不廣，鮮為人知。

[2011.11152] On the Overlooked Pitfalls of Weight Decay and How to Mitigate Them: A Gradient-Norm Perspective

它的思路也很簡單，通過匯總整個模型的參數信息，按照參數權重占比估算出每一層的衰減權重。

而有另一篇論文從另一個新穎的角度提出了一個方案。

[2103.06583] Preprint: Norm Loss: An efficient yet effective regularization method for deep neural networks

它的思路是在每次更新時，從權重中減去一個單元范數權重，可以近似看做是為權重衰減提供了范數先驗。

而后，將正則化從“加性懲罰”轉變為“約束優化”  Constrained Parameter Regularization (CPR) 

[2311.09058] Improving Deep Learning Optimization through Constrained Parameter Regularization

CPR 作為替代權重衰減的替代方案，就是為了權重衰減的調參困局，但請慎用。

為了改善權重衰減帶來的收斂變慢問題，Cautious Weight Decay 隨即也被提出。

[2510.12402v1] Cautious Weight Decay

思路比較簡單，偽代碼一眼就能看懂。

grad = m / (torch.sqrt(v) + epsilon)
m = (p * grad).sign_().clamp_min_(0)
cautious_weight_decay = weight_decay * m

它的靈感多半來自此：

[2411.16085v3] Cautious Optimizers: Improving Training with One Line of Code

至于m要不要改寫成 m / (m.mean()+eps)，用在不同優化器內部性質不太一樣，

如果是Adam理論上可以不做這個操作，但如果用在SGD里，為了穩定性，可以考慮 m / (m.mean()+eps) 。

實在不確定，就實測。

思路出發點都是考慮方向的一致性。

一個作用在參數，參數與更新梯度的方向，一個作用在梯度，當前梯度與平滑梯度的方向。

真的是萬變不離其宗，但凡能作用在梯度的，理論上也能作用在參數。

5.5 學習率熱身與梯度裁剪

在說到Adam過擬合的時候，我們很容易就發現了一個問題。

在不同的模型架構，訓練的每個階段，每層權重的值域是不一樣的，而且這個值域隨著訓練的增加，也一直在變化。

由于這個核心問題的存在，訓練早期梯度的波動就會很大，這個時候通常就需要學習率調參，或者在模型內部加入歸一化層，目的盡可能快地把每一層的值域確立下來。

由此就引發出來學習率熱身以及梯度裁剪相關的思考。

學習率熱身相關的資料和論文也有很多，這里不展開細講。

學習率規劃熱身的基本邏輯都是：

早期用極其小的學習率進行預熱訓練 → 中期慢慢地增大學習率 → 后期再固定學習率或者慢慢減少學習率

雖然很傻，但是確實有效。

21年的時候谷歌為了把歸一化層刪掉，就提出了自適應梯度裁剪方案。

[2102.06171] High-Performance Large-Scale Image Recognition Without Normalization

思路也很簡單，根據每層梯度和權重的值域，按比例縮放當前的梯度。

25年終于有人想要把學習率預熱刪掉。

[2505.21910] Taming Transformer Without Using Learning Rate Warmup

思路跟Scheduled (Stable) Weight Decay很像，只不過這次是作用在學習率上罷了。

本質就是根據每層權重梯度比例算出來一個全局學習率的縮小率。由于每層的激活函數不一樣，算出來一個全局縮小率，從邏輯上其實很牽強。

當然除此之外還有其他類似的思路，例如：

梯度范數化

[1711.02257v4] GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks

def gradient_normalization(grad, eps: float = 1e-8):  
    grad.div_(grad.norm(p=2) + eps)

層范數化縮放

[1904.00962v5] Large Batch Optimization for Deep Learning: Training BERT in 76 minutes

def layer_norm_adaptation(grad, var):
    w_norm = var.norm(p=2)
    g_norm = grad.norm(p=2)
    grad.mul_(torch.where(torch.greater(w_norm, 0),
                       torch.where(torch.greater(g_norm, 0), (w_norm / g_norm), 1.0),
                       1.0))

梯度中心化

[2004.01461v2] Gradient Centralization: A New Optimization Technique for Deep Neural Networks

def centralize_gradient(grad):  
    if grad.dim() > 1:  
        grad.data.add_(-grad.mean(dim=tuple(range(1, grad.dim())), keepdim=True))

林林總總，大同小異。

博主根據自己的理解，也寫了個梯度軟裁剪，代碼如下。

@staticmethod
def _soft_clip(grad, var, epsilon=1e-12):
    dim = None if (r := var.dim()) <= 1 else tuple(range(1, r))
    var_norm = var.square().mean(dim=dim, keepdim=True).sqrt_().clamp_min_(epsilon)
    grad_norm = grad.square().mean(dim=dim, keepdim=True).sqrt_().clamp_min_(epsilon)
    clipped_norm = grad_norm.clamp_max(var_norm)
    return grad.mul_(clipped_norm / grad_norm)

5.6 如何進一步加速訓練收斂

前面已經提到不少關于調參，穩定性問題，但大多數人最關心的還是怎么加速訓練。

主要的思路，基本上就是根據上一步的梯度信息，結合當前步的梯度，在兩步之間求出一個合理的方向，往這個方向再走一步。

這樣做有個好處，就是可以結合上一步的位置進一步修正方向，其實就是殘差加權的路子。

[1909.11015v4] diffGrad: An Optimization Method for Convolutional Neural Networks

[2106.11514v3] Rethinking Adam: A Twofold Exponential Moving Average Approach

有前后梯度交替的做法，自然也就有參數交替的做法。

[1907.08610v2] Lookahead Optimizer: k steps forward, 1 step back

[2103.17182v5] Positive-Negative Momentum: Manipulating Stochastic Gradient Noise to Improve Generalization

但這兩種做法都有一個弊端，就是需要多存一份參數，顯存又要不夠用了。

當然如果不考慮顯存占用問題，

也可以采用Grünwald-Letnikov(G-L)分數階導數，它利用分數階微積分的全局記憶，

將參數更新的梯度替換為G-L分數階近似梯度，從而更好地利用過去的長期曲率信息。

An Adaptive Learning Rate Deep Learning Optimizer Using Long and Short-Term Gradients Based on G–L Fractional-Order Derivative | Neural Processing Letters

在某些場景下，算力充足，也是一種選擇。

如果考慮顯存有限的話，

有一個折中的做法，Nesterov momentum，Adam升級為NAdam，它的思路也很簡單"先沿慣性走一步，再看新梯度，沿修正后的方向走"，也就是從Adam的"看一步走一步"變成了"看一步想兩步"。

Incorporating Nesterov Momentum into Adam | OpenReview

m_nesterov = m * beta1 + grad * (1.0 - beta1)
grad = m_nesterov / sqrt(v)

但是總感覺有點牽強，結合上面提到了各種巧思手段，隨即就有人想到了梯度范數也是一種先驗。

對梯度范數進行指數加權平均，根據這個信息，動態調整梯度，換言之也就是動態調整學習率。

[2210.06364v1] AdaNorm: Adaptive Gradient Norm Correction based Optimizer for CNNs

但這個思路也潛藏著一個弊端，跟v一樣的問題，

訓練后期，激進加速，不但沒有獲得應有的收益，反而會引發不穩定，最終跑偏。

只能說力的作用是相互的，給它一個推力的時候，一定要設置一個相應的阻力去制衡，達到相對穩態。

似乎一切都在往更理想的方向推進著。

看到這里，我相信有很多同學會問，加大學習率，難道不能加速訓練收斂嗎？

我的回答是，能，只有一個前提條件，就是batch size足夠的大，且優化器算法足夠的穩健。

因為看的信息足夠多，用大學習率，直接邁大一步，是肯定沒有問題的。

這個博主已經經過驗證，實測過了。

大多數情況下，我們看到訓練加速，損失飛快地降，不存在過擬合的話，絕大多數都是模型正在調整權重到對應的值域范圍。

假設你使用了Sigmoid激活函數，輸入的值在 [-6,6]左右的區間，對應的輸出值是(0.0025, 0.9975)。

也就是說在Sigmoid的前一層，至少是[-6,6]的值域，才有信息能往后傳。

如果你在Sigmoid前面野蠻地采用了歸一化，卻不進行縮放加權，放大它的值。那這個神經元基本上處于失活的狀態。

所以理想的情況下在進入Sigmoid前手動放大值域，也算是一種先驗，至于放大3.0，放大6.0那就看Sigmoid前一層到底做了什么了。

看到這里，我相信應該沒有人會問歸一化層到底應該加在哪里合適了吧。

這里只是便于理解，舉了個小例子。

經常會有人問Muon這個基于矩陣正交化的優化器，實測為什么沒有傳說中那么高效。

[2502.16982v1] Muon is Scalable for LLM Training

你都已經看到這里了，Muon是個什么玩意，你別跟我說，你心里沒數。

以上，初稿寫于2025.10.06。

商業轉載請聯系作者進行授權，非商業轉載請注明出處。

若有各種其他問題可以通過以下方式聯系博主交流學習。

微信: Dbgmonks
QQ: 200759103
郵箱: gaozhihan@vip.qq.com

注: 不注明來意者一律拒絕。

博主目前進度:

•  無需熱身階段
•  免調學習率
•  無需歸一化層
•  修正梯度累積，實現等效大批次性能
•  緩解長尾梯度
•  加速訓練收斂
•  低顯存占用

License

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.