CSP-S模擬36
T1:島嶼(island)
思路:
依據(jù)亂七八糟的題意,我只能說啥也看不出來。
那咋辦?
(涼拌番茄炒蛋) 只能手模樣例唄
樣例 \(1,2,3\) 全是特殊點,我們直接來看樣例 \(4\)
先畫個圖:

嗯...啥也看不出來。按著題意這圖應(yīng)該有點像二分圖啊,咋不像捏?要不我們換種畫法?
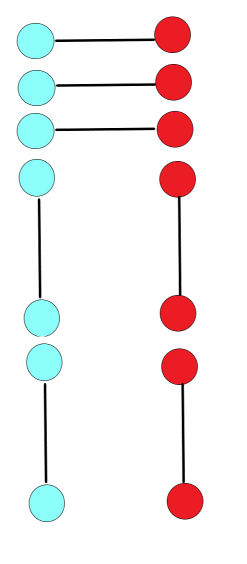
欸,這圖就很二分圖了。但是二分圖還沒學(xué)完咋辦?
那就先找找規(guī)律唄。
為了方便描述,我們給點分下類(才不要叫什么成人兒童呢,有悖人倫)
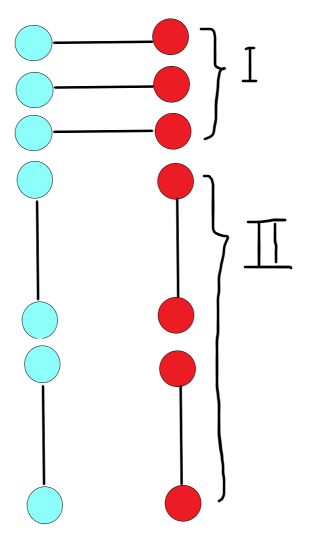
我們先隨便畫出一種情況:
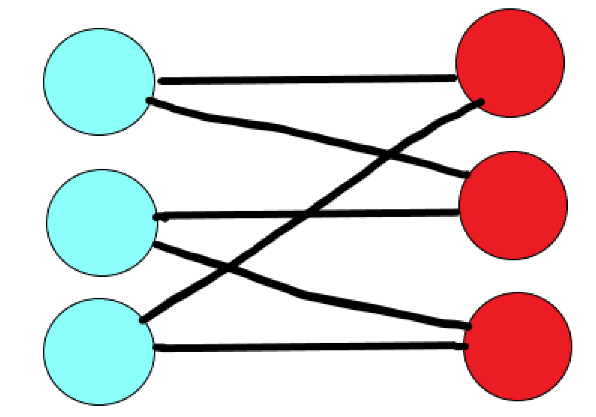
我們可以對這種情況進行拆分,把它視為

和
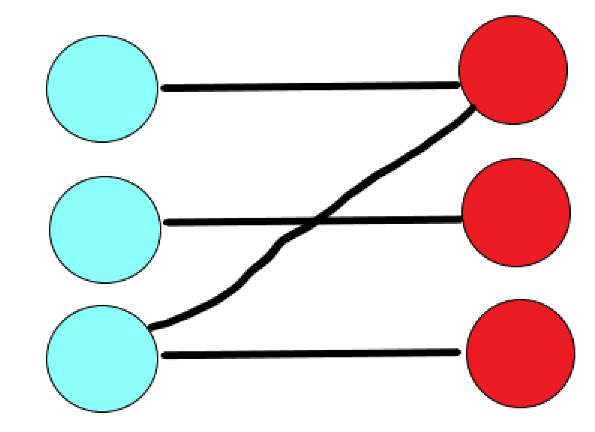
的結(jié)合體。
對于第一張圖,我們可以把它縮為一個 Ⅰ 號節(jié)點,即可以轉(zhuǎn)化為一個 Ⅰ 號節(jié)點連向它本身。
究其本質(zhì),我們可以發(fā)現(xiàn),
對于每一個 Ⅰ 號藍色節(jié)點,
假如它連向本身,那它將會貢獻一個聯(lián)通塊的數(shù)量,這時的概率為 \(\frac{1}{7}\) (一共有七個紅色節(jié)點)。
假如它連向一個 Ⅰ 號紅色節(jié)點(非本身),那它會和那個節(jié)點所在邊形成一個新的 Ⅰ 號節(jié)點而無貢獻。
假如它連向一個 Ⅱ 號紅色節(jié)點,那它會和那個節(jié)點所在邊形成一個新的 Ⅱ 號節(jié)點而無貢獻。
綜上,不難發(fā)現(xiàn),一個 Ⅰ 號節(jié)點只有連向自身才有貢獻。
又因為我們從上向下考慮,所以可選擇的節(jié)點數(shù)逐漸減少,所以下面的點貢獻的概率會增大。
對于每一個 Ⅱ 號藍色節(jié)點,(此時我們已經(jīng)處理完所有的 Ⅰ 號點)
假如它只連一條邊,那會形成一個新的 Ⅰ 而不會有貢獻。
假如它連向同一個 Ⅱ 號紅色節(jié)點,那它會和那兩個節(jié)點所在邊形成一個連通塊 ,這時的概率為 \(\frac{1}{4}\) (因為 Ⅰ 號節(jié)點處理完了)
假如它連向兩個不同的 Ⅱ 號紅色節(jié)點,那它會和那兩個節(jié)點所在邊形成新的 Ⅱ 號紅色節(jié)點而無貢獻。
綜上,對于一個 Ⅱ 號節(jié)點,當(dāng)它連向同一個 Ⅱ 號節(jié)點時才會產(chǎn)生貢獻。
然后代碼就好寫啦~~
代碼:
$code$
#include<iostream>
using namespace std;
double x,y,n,ans;
signed main(){
// freopen("island.in","r",stdin);
// freopen("island.out","w",stdout);
ios::sync_with_stdio(false);
cin>>x>>y;
n=2*x+y;
while(y--) ans+=1.0/n,n--;
while(x--) ans+=1.0/(n-1),n-=2;
printf("%0.16lf",ans);
return 0;
}
T2:小朋友(xiao)
思路:
由于數(shù)據(jù)較小,所以會有多種解法。這里只提供兩種思路。
一、
直接搜索顯然是不好搜的,因為最優(yōu)串的長短是不固定的。但是在偷偷瞄一眼數(shù)據(jù), $ n ≤ 50 $,我們?yōu)槭裁床幻杜e每一種長度下的最優(yōu)解,最后取 \(max\) 不就行了。
由于我們要的是字典序最大的排列,所以可以從大到小枚舉每一位是哪個字母,然后看看 \(s\) 或 \(t\) 字符串里是否有這個字母,如果有就加上,沒有就不行。
反正這個搜索也是蠻奇特的,沒想過有朝一日還能用 \(string\) 作為函數(shù)的返回類型。
代碼:
$code$
#include<iostream>
#include<algorithm>
using namespace std;
const int N=55;
string s,t,ans[N];int len,n;
inline string dfs1(int x,string css){
if(css.size()>=n) return css;
for(char i='z';i>='a';i--){
int l=css.size()-n+s.size();
for(int j=x;j<=l;j++){
if(s[j]==i){
return dfs1(j+1,css+i);
}
}
}
}
inline string dfs2(int x,string css){
if(css.size()>=n) return css;
for(char i='z';i>='a';i--){
int l=css.size()-n+s.size();
for(int j=x;j<=l;j++){
if(t[j]==i&&ans[n][css.size()]==s[j]){
string zyq=dfs2(j+1,css+i);//這個變量名毫隨便寫的 寫啥都行
if(zyq!="fanxintong") return zyq;//同上(不過最好別罵人)
}
}
}return "fanxintong";
}
int main(){
// freopen("xiao.in","r",stdin);
// freopen("xiao.out","w",stdout);
ios::sync_with_stdio(false);
cin>>s>>t;
int len=s.size();
for(int i=1;i<=len;i++){
n=i;
ans[i]=dfs1(0,"");
ans[i]+=dfs2(0,"");
}
sort(ans+1,ans+1+len);
cout<<ans[len];
return 0;
}
二、
上面也說了,那種做法基于數(shù)據(jù)超級無敵小的情況。所以,咱們再來一版阿德民做法(一不小心成最優(yōu)解了)。時間復(fù)雜度為 \(O(n^3)\) 的。
我們設(shè) \(f_i\) 表示前 \(i\) 位最大的 \(s\) 的子序列,\(g_i\) 表示前 \(i\) 位最大的 \(t\) 的子序列。
我們可以先遍歷 \(s\) 和 \(t\),然后遍歷 \(f\) 和 \(g\) ,看看把這一位放在前面最大的子序列的后面是否會更優(yōu)。若會則記錄下來,若不會則跳過。
最后的答案就是 \(f+g\) 取 \(max\) 。
代碼:
$code$
#include<iostream>
#include<cstring>
using namespace std;
const int N=55;
char s[N],t[N];
string f[N],g[N],ans;
int main(){
// freopen("xiao.in","r",stdin);
// freopen("xiao.out","w",stdout);
ios::sync_with_stdio(false);
cin>>(s+1)>>(t+1);
int n=strlen(s+1);
for(int i=1;i<=n;i++){
for(int j=i;j>=0;j--){
string x=f[j]+s[i],y=g[j]+t[i];
if(x>f[j+1]) f[j+1]=x,g[j+1]=y;
else if(x==f[j+1]&&y>g[j+1]) g[j+1]=y;
}
}
for(int i=1;i<=n;i++) ans=max(ans,f[i]+g[i]);
cout<<ans;
return 0;
}
T3:列表(list)
沒改完,\(But\) ...先存著
暫存$code$
#include<iostream>
#define lid id<<1
#define rid id<<1|1
using namespace std;
const int N=4e5+5;
int n,m,a[N],p[N],ans;
struct node{int l,r,lazy,max;}tr[N<<2];
inline void pushdown(int id){
tr[lid].lazy+=tr[id].lazy;tr[lid].max+=tr[id].lazy;
tr[rid].lazy+=tr[id].lazy;tr[rid].max+=tr[id].lazy;
tr[id].lazy=0;
}
inline void build(int id,int l,int r){
tr[id].l=l;tr[id].r=r;
if(l==r){
tr[id].max=-l;
return ;
}
int mid=(l+r)>>1;
build(lid,l,mid);build(rid,mid+1,r);
tr[id].max=max(tr[lid].max,tr[rid].max);
}
inline void update(int id,int l,int r,int val){
if(tr[id].l>r||tr[id].r<l) return ;
if(l<=tr[id].l&&tr[id].r<=r){
tr[id].lazy+=val;
tr[id].max+=val;
return ;
}
pushdown(id);
update(lid,l,r,val);
update(rid,l,r,val);
tr[id].max=max(tr[lid].max,tr[rid].max);
}
int main(){
ios::sync_with_stdio(false);
cin>>n;
m=2*n+1;
n++;
for(int i=1;i<=m;i++){
cin>>a[i];
p[a[i]]=n-abs(n-i);
}
build(1,1,n);
for(int i=1,r=1;i<=m;i++){
while(r<=m&&tr[1].max<=0) update(1,p[r++],n,1);
ans=max(ans,r-i-(tr[1].max>0));
update(1,p[i],n,-1);
}
cout<<ans<<'\n';
return 0;
}


