分支界限(B&B Branch And Bound)也是一種編程范式,在離散組合性質問題上的最優解問題通常可以用分支界限方法進行求解,與回溯有相同之處,它也是枚舉所有備選項,但是回溯是一種遍歷所有可能解的結構,這種枚舉通常是暴力型的,是不太聰明的枚舉;分支界限是一種渦輪增壓性的枚舉(turbo-charged enumeration),是一種聰明型的枚舉,它也是列舉并勾選所有可行結果,但是它采用“提前量”手段讓自己的下一步選擇看起來更為明智。有一些概念需要理解一下:
1、界限(Bound): 就是條件限制,也就是邊界值
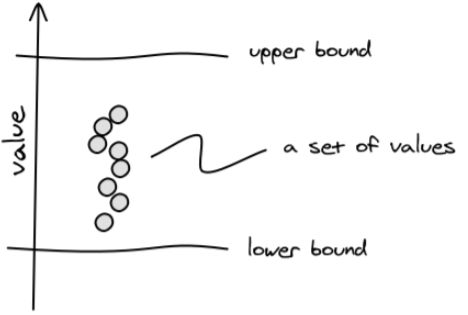
例如一個數值集合中,如上圖,這個集合一定會有一個上限和一個下限:
上限(upper bound):大于等于集合中最大值的數。
下限(lower bound):小于等于集合中最小值的數。
上限和下限是根據目標函數和條件函數共同確定的,計算按照系數比例值對未知量進行排序重組,然后進行相關計算,例如:
目標函數:8x1 + 11x2 + 6x3 + 4x4
條件函數:5x1 + 7x2 + 4x3 + 3x4 ≤ 14
其中x1,x2,x3,x4變量的系數比例值是:1.6,1.571,1.5,1.3,已經按照從大到小的順序排好了,按照條件函數,可以得知:
(x1,x2,x3,x4)=(1,1,0.5,0),maxVal=22
(x1,x2,x3,x4)=(0,1,1,1),minVal=21
=>最優解的上線是22,下限是21 !x只能取整數
界限(bound)的確定對問題的求解有很大的影響,界限值可以在計算的過程中逐步計算出來。
2、分支(Branch): 構建一個解的空間樹,但是構造過程是有條件的,一個節點能否還能構造子樹,需要看該節點是否有產生更優解的“潛質”,如果這個節點不滿足界限條件或者不能產生最優解,則將該節點直接拋棄,也就相當于切除該分支,不再進行遍歷。
分支界限在求解過程中有一些虛擬概念產生,搬取教科書的內容解釋如下:
1、激活:搜索到某個結點的時候,該結點就被激活,是一個動作。
2、死結點:所有子結點已經全部被搜索完或者自身條件不滿足界限條件的結點。
3、活結點:已被激活或者還未被激活的結點。
4、E-結點:擴展結點,當前正在搜索其孩子的結點。
分支界限的基本思想描述如下:
1、創建一個活結點表B,可用某個list數據結構進行表述
2、將狀態空間樹的根結點放到活結點表B中
3、初始化當前最優解bsv
while isNotEmpty(B):
//從B表中獲取某個結點,并將其從B表中刪除
E-node=B.remove(0);//B表可以是排好序的,可以按照最小消費/最大比值等進行排序
if E-node 具有當前最優解
bsv=E-node.value;//更新最優解
for each son of E-node:
if 當前孩子結點滿足約束條件并且目標函數的當前界限:
激活當前孩子結點,并將其放到B表單中。
else:
將當前結點剪枝,也就是不將當前結點放到B表單中。
以上算法描述中有一個關鍵點,就是目標函數的當前界限,這里用0-1背包進行描述,以下是一個簡單的圖示:

上圖中,標紅的結點可以被剪枝,不再對其進行擴展,為什么呢?紅結點的當前值是0,可選值只有一個12,因為存在一個結點結點的值是16,它
比12要大,所以從紅結點擴展出的值肯定不是最優解,所以也就沒必要再進行擴展了。這就是剪枝,此時目標函數的當前界限是16,如果一個結點的當前值
和它可選的值的小于這個值的話,那么那個結點就沒必要再進行擴展了。
以上空間樹的構造同樣是一個抽象的概念,在計算的過程中不需要創建真實的樹結構,但是我們對其的描述需要用樹進行描述。其中結點值有很多不同的狀態,比如:當前重量、當前值、當前解,這里可用一個結點進行描述,這里給出一個0-1背包的解法:
def Node:
int[] result;//結果
int weight;//當前重量
int value;//當前值
int possibility;//還可以取的可能值
int depth;//樹的深度,用于判斷是否到葉結點了
def knapspack:
capacity=5
value=[6,10,12]
weight=[1,2,3]
maxValue=-1;//記錄最大值
result=[];
inittialNode=new Node();
initialNode.possibility=sum(value);//初始化可能值
list<Node> temp=new ArrayList<>()
temp.add(initialNode);//初始化活結點
while isNotEmpty(temp):
node=temp.remove(0);
if maxValue<node.value://更新最優解
maxValue=node.value;
result=node.result;
if temp.size()>0:
maxPossibility=node.value+possibility;//最大的可能值
// 判斷界限值,如果滿足條件,則進行剪枝
if maxPossibility < temp集合中任意一個結點的value值:
node=null;
continue;//剪枝
depth=node.depth+1;//進行下一層的遍歷
//判斷是否已經到達葉子結點:
if depth < value.length:
//更新左孩子值
node.possibility=node.possibility-value[depth];
node.depth=depth;
temp.add(node);
//判斷右孩子的值是否滿足約束條件,如果不滿足條件,則進行剪枝
if node.weight+weight[depth]<capacity:
Node rightNode=new Node();
rightNode.possibility=node.possibility-value[depth];
rightNode.weight=node.weight+weight[depth];
rightNode.depth=depth;
rightNode.result=node.result;
//將當前值放到結果值中,以便于記錄結果值
rightNode.result[depth]=value[depth];
//記錄當前的結果值的和
rightNode.value=sum(rightNode.result);
temp.add(rightNode);
//這里可以對temp進行排序,可以用possibility進行排序,哪個結點更有可能產生最優解,哪個結點放到前面
sortByPossibility(temp);
return maxValue and result;
上述偽代碼中標紅的地方是計算過程中動態界限值產生的地方,而且上述代碼中只會返回一個最優解。
分支界限算是回溯方法的一個增強版,但是其難點在于界限值的計算,它是根據當前已有的值和后續可能取值的最大和與當前其他節點的值進行計算,如果某個節點的可計算的可行解比當前其他節點的值要小,那就沒有擴展的必要了,需要進行剪枝了;還有,如果當前節點不滿足約束條件,也需要直接剪枝。分支界限的經典之處就是預判某個節點是否具有展開的價值,如果沒有,則直接排除掉這個節點。所以它的遍歷要比回溯法少,如果約束條件和界限值收斂的好的話,則其效果更好。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號