ABC369 C-G題解 (AtCoder Beginner Contest 369)
C
對于一個等差數列，它里面包含的等差數列（取這個數列的第i位~第j位），必定也是等差數列。
尋找等差數列的時候，如果一個等差數列，向最左/最右加1個數后，仍是等差數列，則把它們加上。從而尋找所有場上的等差數列，必定是不重疊的，等差數列彼此獨立。
從而可以從1遍歷到n，O(n)復雜度。
對于每一段等差數列，只統計里面包含的長度大于等于2的等差數列。最后再加上長度等于1的等差數列，即為單獨的每個數，為n。這樣，思路會清晰一點
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 #define ULL unsigned long long 5 6 const LL mod_1=1e9+7; 7 const LL mod_2=998244353; 8 9 const double eps_1=1e-5; 10 const double eps_2=1e-10; 11 12 const int maxn=2e5+10; 13 14 LL a[maxn]; 15 16 int main() 17 { 18 LL n,i,j,d; 19 LL sum=0; 20 cin>>n; 21 for (i=1;i<=n;i++) 22 cin>>a[i]; 23 j=1; 24 for (i=1;i<n;) 25 { 26 d=a[i+1]-a[i]; 27 j=i; 28 i++; 29 while (i<n && a[i+1]-a[i]==d) 30 i++; 31 sum+=1LL*(i-j)*(i-j+1)/2; 32 } 33 cout<<sum+n; 34 35 return 0; 36 }
D
DP
寫成數組形式，好理解一點，寫少一點代碼
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 #define ULL unsigned long long 5 6 const LL mod_1=1e9+7; 7 const LL mod_2=998244353; 8 9 const double eps_1=1e-5; 10 const double eps_2=1e-10; 11 12 const int maxn=2e5+10; 13 14 LL f[maxn][2]; 15 16 17 int main() 18 { 19 LL n,i,a; 20 f[0][0] = 0; 21 f[0][1] = -1e18; 22 cin>>n; 23 for (i=1;i<=n;i++) 24 { 25 cin>>a; 26 f[i][0] = max(f[i-1][0], f[i-1][1] + a*2); 27 f[i][1] = max(f[i-1][1], f[i-1][0] + a); 28 } 29 30 cout<<max(f[n][0],f[n][1]); 31 return 0; 32 }
E
floyd 求兩兩每個點之間的距離 + dfs獲得幾個橋所有可能的順序
看到別人有用next_permutation，而且是挺多人用這個，挺不錯。
但是后面，直接一行寫出情況，對于大部分人來說是不是容易寫錯？而且關鍵是挺多人都這樣寫，我感覺比較神奇emmm。我個人，感覺用dfs相對不容易寫錯。
dfs獲得幾個橋所有可能的順序，其實就很像旅行商問題，所有城市都訪問一遍。然后這里是橋可以選擇兩個方向，也不好用狀態壓縮。
g個點，2^g個方向，橋的順序，g!排列組合，每種橋方向類型，g個權值和相加，O(2^g*g!*g) 19,200 再乘個Q，沒問題
我在比賽的時候，把floyd的順序搞反了，然后幾天找不到問題，真的繃不住了！！！floyd算法，三重循環的順序問題，不要寫錯了 - congmingyige - 博客園 (cnblogs.com)
1 /* 2 n,m的大小，對應創建數組的大小，不要弄混，特別是這類題，n<=400，m<=2e5，提交前要檢查一遍。當RE的時候，就要第一時間意識到數組大小設置錯誤的問題 3 4 怎么也調不出問題，包括檢查代碼，造樣例，看題面，就立刻先切換到下一題。沒必要花那么多時間耗在上面，否則檢查錯誤，采用錯誤的方法，做很多無用功。而且影響做題時間和效率。這些時間，今早做下一題，有可能就做出來其它題了 5 做選擇，要么全攻下一題（意識到難發現錯誤在哪，立刻切換，檢查時間不要太長），要么剩下這些時間，全力檢查這一題，不要既這又那 6 用assert等方式找一下問題所在，還有造一下大樣例 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 #define LL long long 11 #define ULL unsigned long long 12 13 const LL mod_1=1e9+7; 14 const LL mod_2=998244353; 15 16 const double eps_1=1e-5; 17 const double eps_2=1e-10; 18 19 const int maxn=4e2+10; 20 const int maxm=2e5+10; 21 22 LL u[maxm],v[maxm],t[maxm],dist[maxn][maxn],b[10],g,n,result; 23 bool vis[10]; 24 25 void dfs(LL d, LL ans, LL road) 26 { 27 LL i,j; 28 if (ans==g) 29 { 30 result = min(result, road+dist[d][n]); 31 return; 32 } 33 for (i=1;i<=g;i++) 34 if (vis[i]==0) 35 { 36 j=b[i]; 37 38 vis[i]=1; 39 dfs(v[j], ans+1, road+dist[d][u[j]] + t[j]); 40 vis[i]=0; 41 42 vis[i]=1; 43 dfs(u[j], ans+1, road+dist[d][v[j]] + t[j]); 44 vis[i]=0; 45 } 46 } 47 48 int main() 49 { 50 LL m,q,i,j,k; 51 cin>>n>>m; 52 for (i=1;i<=n;i++) 53 for (j=1;j<=n;j++) 54 dist[i][j] = 1e15; 55 for (i=1;i<=n;i++) 56 dist[i][i]=0; 57 for (i=1;i<=m;i++) 58 { 59 cin>>u[i]>>v[i]>>t[i]; 60 dist[ u[i] ][ v[i] ] = dist[ v[i] ][ u[i] ] = min(dist[ u[i] ][ v[i] ], t[i]); 61 } 62 63 for (k=1;k<=n;k++) 64 for (i=1;i<=n;i++) 65 for (j=1;j<=n;j++) 66 dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j]); 67 /* 68 for (i=1;i<=n;i++) 69 for (j=1;j<=n;j++) 70 assert(dist[i][j]<1e15); 71 */ 72 73 cin>>q; 74 while (q--) 75 { 76 cin>>g; 77 for (i=1;i<=g;i++) 78 cin>>b[i]; 79 memset(vis,0,sizeof(vis)); 80 result=1e18; 81 dfs(1,0,0); 82 //assert(result<1e18); 83 cout<<result<<endl; 84 } 85 86 return 0; 87 } 88 /* 89 g個點 90 2^g個方向，橋的順序，g!排列組合，每種橋方向類型，g個權值和相加，O(2^g*g!*g) 19,200 再乘個Q，沒問題 91 */
F
應該看一下題面，在剩余1個小時的時候，這樣才有時間做和取舍（題D、E)
這種屬于題面很容易理解，也很容易想到解法的。就是寫的過程中容易寫錯，debug也是，需要時間長一點
感覺這是高手和某類菜鳥的區別。某類菜鳥也可以很快找到解法，就是寫代碼和調試代碼的時候，對于這類比較瑣碎的代碼，需要寫挺久
能想到的基礎題目是用DP做，二維方格，dp[i][j]=max(dp[i-1][j], dp[i][j-1])。
現在是n、m相乘比較大，然后硬幣數比較少。
因為只能向下或者向右，所以對于一個點，只有列的數值小于等于它的點，才能訪問到它。這容易想到樹狀數組。同樣，對于行，也是只有行的數值小于等于它的點，才能訪問到它。
f[i]= max(f[j]) + 1。 i表示這個點的列數值為i，j是所有小于i的數，用樹狀數組獲取f數組里1~i的最大值。
按照硬幣行數值優先，然后列數值優先的順序排序，然后依次訪問硬幣。可以確保，對于該硬幣，前面的硬幣的行都是小于等于它，后面的硬幣的行都是大于它，或者行等于它但是列大于它，無法從后面的硬幣到該硬幣。
1 /* 2 應該看一下題面，在剩余1個小時的時候，這樣才有時間做和取舍（題D、E) 3 這種屬于題面很容易理解，也很容易想到解法的。就是寫的過程中容易寫錯，debug也是，需要時間長一點 4 感覺這是高手和某類菜鳥的區別。某類菜鳥也可以很快找到解法，就是寫代碼和調試代碼的時候，對于這類比較瑣碎的代碼，需要寫挺久 5 6 用xpre,ypre,x,y，這樣變量不容易搞錯。還有，找問題的，多檢查一下變量，這種變量最容易寫錯 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 #define LL long long 11 #define ULL unsigned long long 12 13 const LL mod_1=1e9+7; 14 const LL mod_2=998244353; 15 16 const double eps_1=1e-5; 17 const double eps_2=1e-10; 18 19 const int maxn=2e5+10; 20 21 pair<int,int> par[maxn]; 22 23 map<pair<int,int>, pair<int,int> > mp; 24 25 pair<int, int> pre[maxn]; 26 int f[maxn]; 27 vector<string> vec; 28 29 void add_path(pair<int,int> dpre, pair<int,int> d) 30 { 31 int i,j; 32 string str=""; 33 for (i=dpre.first;i<d.first;i++) 34 str+='D'; 35 for (j=dpre.second;j<d.second;j++) 36 str+='R'; 37 vec.push_back(str); 38 } 39 40 void dfs(pair<int,int> d) 41 { 42 pair<int,int> dpre; 43 44 dpre = mp[d]; 45 46 if (dpre!=make_pair(-1,-1)) 47 { 48 add_path(dpre,d); 49 dfs(dpre); 50 } 51 else 52 add_path(make_pair(1,1),d); 53 } 54 55 int main() 56 { 57 int h,w,n,x,y,v,i,j,y_max=2e5; 58 pair<int,int> dpre,d; 59 cin>>h>>w>>n; 60 memset(f,0,sizeof(f)); 61 for (i=0;i<n;i++) 62 { 63 cin>>x>>y; 64 par[i] = make_pair(x,y); 65 } 66 sort(par, par+n); 67 68 for (j=0;j<n;j++) 69 { 70 x = par[j].first; 71 y = par[j].second; 72 dpre = make_pair(-1,-1); 73 74 v = 0; 75 for (i=y;i>=1;i-=i&-i) 76 if (f[i]>v) 77 { 78 v=f[i]; 79 dpre = pre[i]; 80 } 81 82 v++; 83 84 if (v>f[y]) 85 { 86 d = make_pair(x,y); 87 mp[d] = dpre; 88 89 for (i=y;i<=y_max;i+=i&-i) 90 if (v>f[i]) 91 { 92 f[i]=v; 93 pre[i]=d; 94 } 95 } 96 } 97 98 v=0; 99 for (i=y_max;i>=1;i-=i&-i) 100 if (f[i]>v) 101 { 102 v=f[i]; 103 dpre=pre[i]; 104 } 105 cout<<v<<endl; 106 add_path(dpre,make_pair(h,w)); 107 dfs(dpre); 108 reverse(vec.begin(), vec.end()); 109 for (auto d:vec) 110 cout<<d; 111 112 return 0; 113 }
學習官方代碼，
vector 初始化，第二個數，就是vector里初始化的數值
LIS，二分的寫法，4行就搞定了？？！！！
對于pre數組，記錄點id，而不是記錄二維坐標，這樣方便一點，寫少一點代碼
用二分的寫法，而不是樹狀數組的寫法，只用修改一次pre，這個點的pre就是數組里上一個點，用樹狀數組，每次+lowbit后，都要判斷修改一次，總感覺代碼量相對比較大，不利索
pre[i] = (it ? id[it - 1] : -1); 這個寫法不錯
官方也是用while、vector記錄從終點出發，不斷pre的點序列，然后用reverse，的確，這個好用。我感覺用dfs，寫得挺不舒服的
1 int now = id[m]; 2 while (now != -1) { 3 path.push_back(coins[now]); 4 now = pre[now]; 5 } 6 path.emplace_back(1, 1); 7 reverse(path.begin(), path.end());
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 int main() { 6 int h, w, n; 7 cin >> h >> w >> n; 8 vector<pair<int, int>> coins; 9 for (int i = 0; i < n; i++) { 10 int r, c; 11 cin >> r >> c; 12 coins.emplace_back(r, c); 13 } 14 sort(coins.begin(), coins.end()); 15 vector<int> dp(n, 1e9), id(n, -1), pre(n); 16 for (int i = 0; i < n; i++) { 17 int it = upper_bound(dp.begin(), dp.end(), coins[i].second) - dp.begin(); 18 dp[it] = coins[i].second; 19 id[it] = i; 20 pre[i] = (it ? id[it - 1] : -1); 21 } 22 int m = n - 1; 23 while (id[m] == -1) --m; 24 vector<pair<int, int>> path = {{h, w}}; 25 int now = id[m]; 26 while (now != -1) { 27 path.push_back(coins[now]); 28 now = pre[now]; 29 } 30 path.emplace_back(1, 1); 31 reverse(path.begin(), path.end()); 32 string s; 33 for (int i = 0; i < (int) path.size() - 1; i++) { 34 int d = path[i + 1].first - path[i].first; 35 int r = path[i + 1].second - path[i].second; 36 while (d--) s.push_back('D'); 37 while (r--) s.push_back('R'); 38 } 39 cout << m + 1 << '\n' << s << '\n'; 40 }
G
我們只需要選擇葉子節點。如果選擇了其它點，那么它的孫子節點必定比它更適合。
記錄點1到某個點的長度，從大到小排序依次取。
取了一個點后，點1到這個點經過的邊，所有的邊值都要修改為0，即點1到其它點經過的邊中，再用到這些邊，也無法增加權值。
暴力做的話，即每個取一個點后，修改受影響的其它點（有與這個點共用邊的），不行。比如這個圖 ，每次拿最左邊的點，然后靠右的點都要受到重新計算權值，要修改的點的數目太多了。
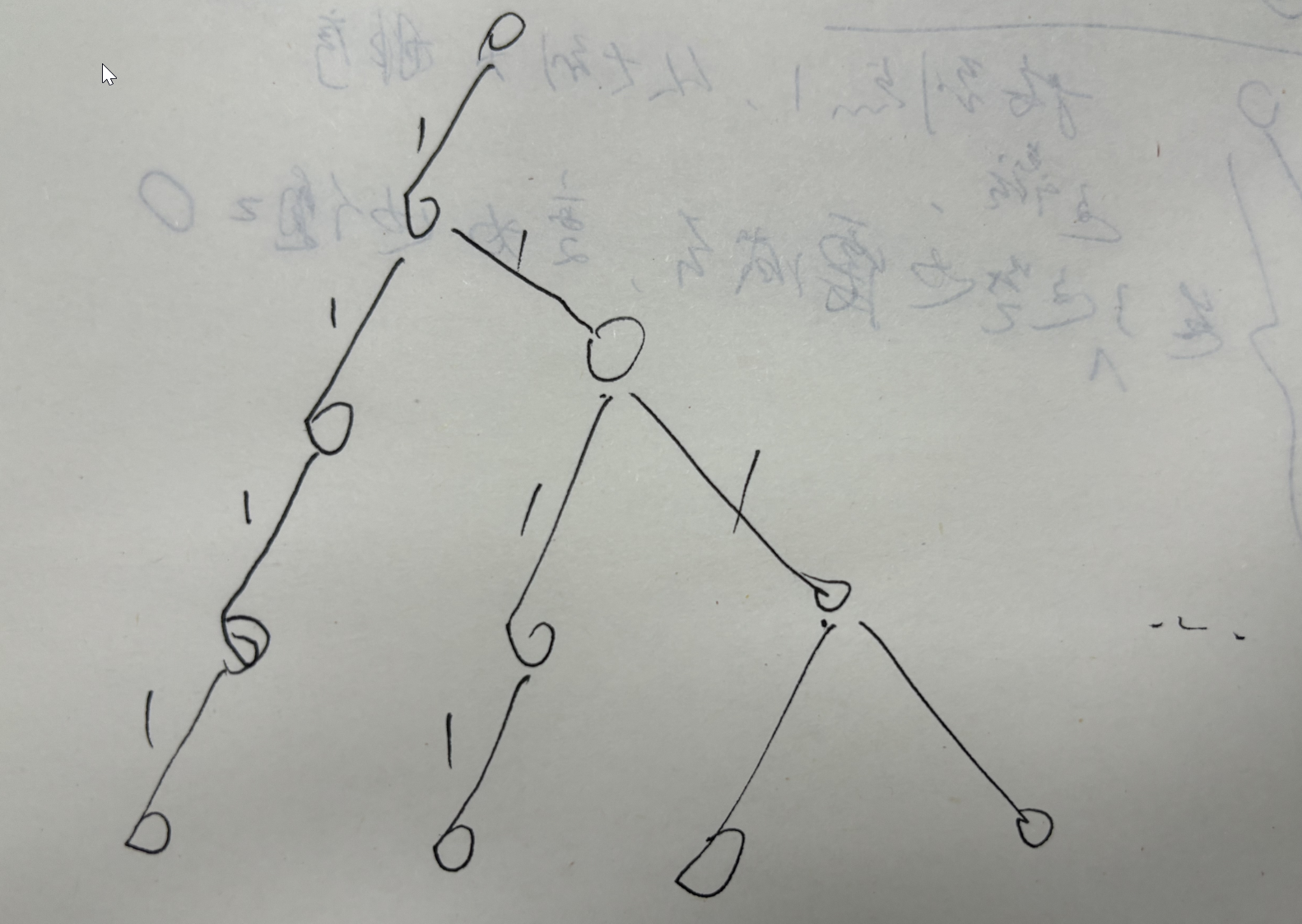
樹的長鏈剖分
區別在于，定義 重子節點 表示其子節點中子樹經過邊權值之和最大的子結點
無論選擇的順序如何（權值大小的排序），我們必定是按照長鏈剖分的方式選擇葉子節點/邊。
我用的方法是，對于一個點的所有子節點，不計算重點（只會有一個或者沒有），剩余其它點，都統計長度（從這個點開始到某個葉節點的路徑），同時，不要遺漏根節點。就比如上圖里，記錄所有白色點為起始的路徑。
Atcoder Beginner Contest 369 - maniubi - 博客園 (cnblogs.com) 這個的代碼，統計輕子節點，放在了dfs函數之外。
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 #define ULL unsigned long long 5 6 const LL mod_1=1e9+7; 7 const LL mod_2=998244353; 8 9 const double eps_1=1e-5; 10 const double eps_2=1e-10; 11 12 const int maxn=2e5+10; 13 14 vector<pair<LL, LL> > adj[maxn]; 15 bool vis[maxn]; 16 LL len[maxn],fa[maxn],ans[maxn]; 17 vector<LL> result; 18 19 void dfs(LL d) 20 { 21 LL child,value,cur_len,hson; 22 vis[d]=1; 23 for (auto single:adj[d]) 24 { 25 child = single.first; 26 value = single.second; 27 28 if (!vis[child]) 29 { 30 dfs(child); 31 32 cur_len = len[child] + value; 33 34 if (cur_len>len[d]) 35 { 36 len[d] = cur_len; 37 hson = child; 38 } 39 } 40 else 41 fa[d] = child; 42 } 43 44 for (auto single:adj[d]) 45 { 46 child = single.first; 47 value = single.second; 48 if (child!=hson && child!=fa[d]) 49 result.push_back(len[child]+value); 50 } 51 } 52 53 int main() 54 { 55 LL n,i,u,v,w; 56 cin>>n; 57 for (i=1;i<n;i++) 58 { 59 cin>>u>>v>>w; 60 adj[u].push_back(make_pair(v,w)); 61 adj[v].push_back(make_pair(u,w)); 62 } 63 64 memset(vis,0,sizeof(vis)); 65 memset(len,0,sizeof(len)); 66 fa[1]=0; 67 dfs(1); 68 69 result.push_back(len[1]); 70 sort(result.begin(),result.end(),greater<LL>()); 71 72 i=0; 73 ans[0]=0; 74 for (auto d:result) 75 { 76 i++; 77 ans[i]=ans[i-1]+d; 78 } 79 i++; 80 while (i<=n) 81 { 82 ans[i]=ans[i-1]; 83 i++; 84 } 85 for (i=1;i<=n;i++) 86 cout<<ans[i]*2<<endl; 87 88 89 return 0; 90 }
學習它這種寫法：
int ans = 0; for (int i = 0; i < n; i ++) { if (i < d.size()) ans += d[i]; cout << ans * 2ll << "\n"; }
浙公網安備 33010602011771號