快速排序及優(yōu)化
快速排序
每次從當(dāng)前考慮的數(shù)組中選一個(gè)元素,把這個(gè)元素想辦法挪到應(yīng)該排好序的位置,比如4這個(gè)元素,它就有一個(gè)性質(zhì)4之前的元素都是小于它的,之后的元素都是大于它的,之后我們要做的事情是對小于4和大于4的數(shù)組分別繼續(xù)使用快速排序的思路,逐漸遞歸下去完成整個(gè)排序過程。

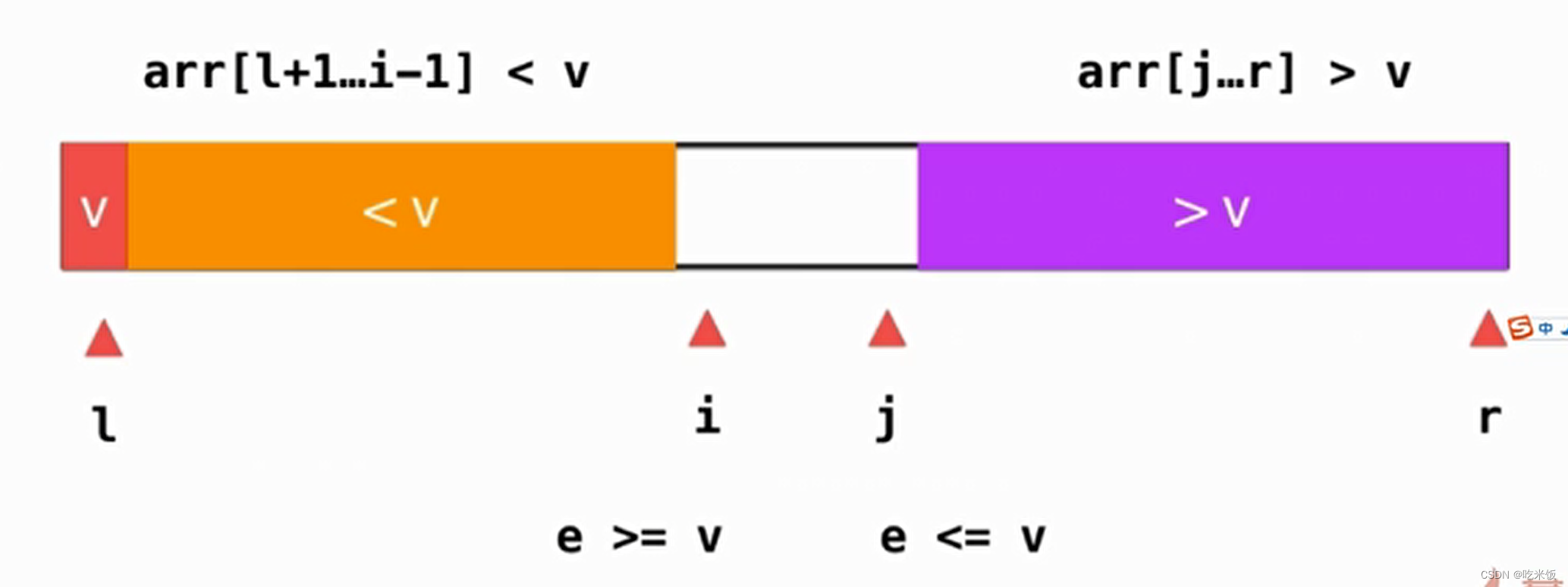
對于快速排序如果把選定的元素挪到正確的位置的過程也是快速排序的核心,在這個(gè)過程中我們通常選擇數(shù)組第一個(gè)元素為我們分界的標(biāo)志點(diǎn),我們記錄這個(gè)點(diǎn)為 l ,之后我們逐漸的遍歷右邊所有沒有被訪問的元素,在遍歷的過程中我們逐漸整理一部分是小于v這個(gè)元素的,一部分是大于v這個(gè)元素的,當(dāng)讓我們要有個(gè)記錄那個(gè)是小于v和大于v的分界點(diǎn),這個(gè)點(diǎn)為 j ,而當(dāng)前訪問的元素記錄為 i。

我們?nèi)绾蝸頉Q定當(dāng)前的元素要怎樣變化才能維持當(dāng)前的性質(zhì),如果當(dāng)前的元素e是比v還要大的,那么他直接就放在大于v一部分的后面。

然后就考慮下一元素就好了。

如果當(dāng)前的元素e是比v還要小的。

我們只需要當(dāng)前橙色部分也就是j所指的位置的后一個(gè)元素和當(dāng)前做考察的元素 i進(jìn)行一下交換 。
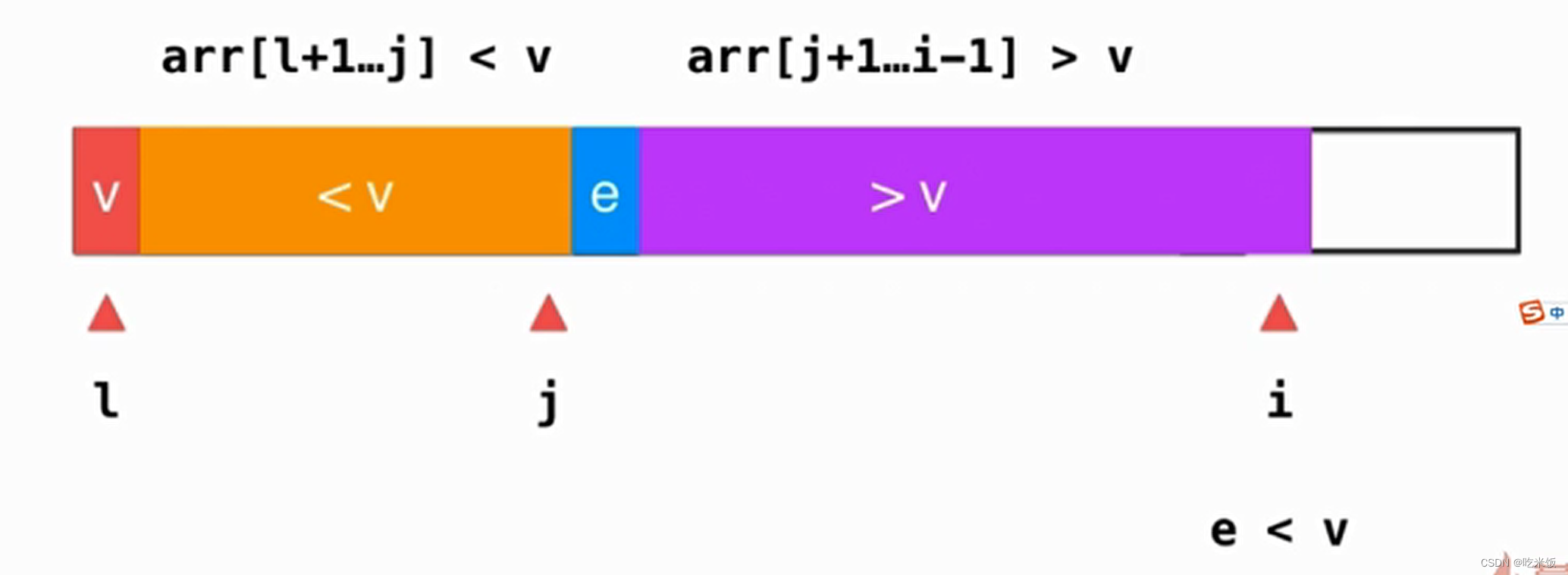
之后我們進(jìn)行一下位置維護(hù) ++j,++i。

以此類推,整個(gè)數(shù)組分成三個(gè)部分,第一個(gè)元素是v,橙色部分小于v,紫色部分大于v。

最后我們需要做的是把數(shù)組 l這個(gè)位置和數(shù)組j這個(gè)位置進(jìn)行交換,這樣整個(gè)數(shù)組就形成了我們設(shè)想的那樣,前面小于v,后面大于v。
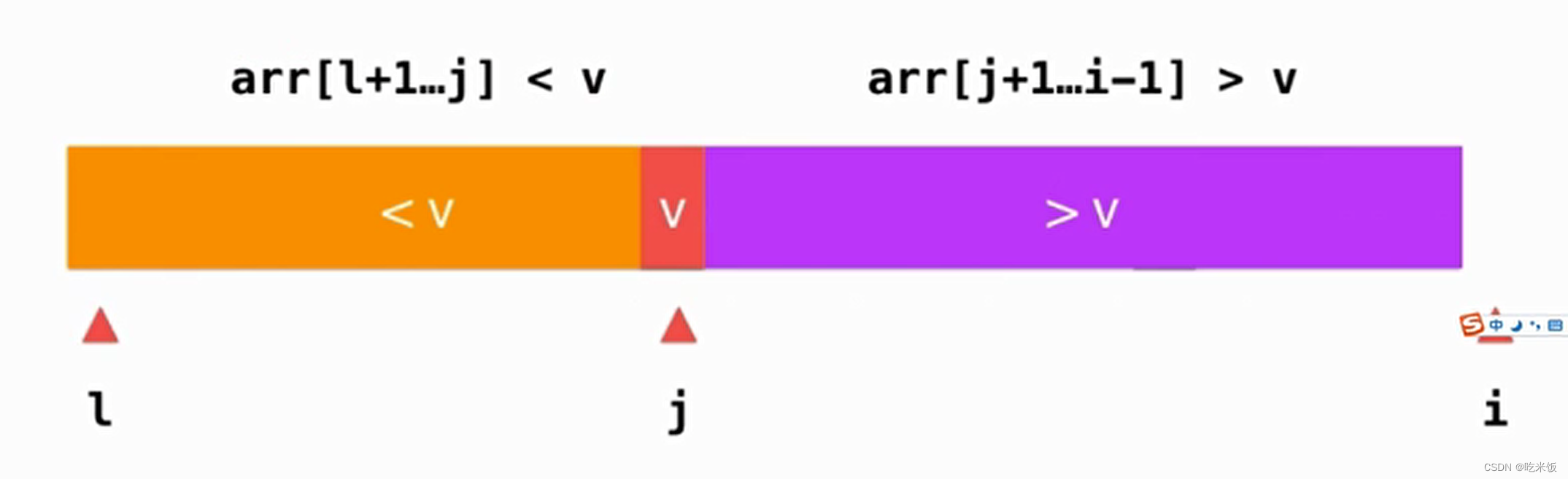
優(yōu)化
- 對于小規(guī)模數(shù)組, 使用插入排序進(jìn)行優(yōu)化;
- 隨機(jī)在arr[l...r]的范圍中, 選擇一個(gè)數(shù)值作為標(biāo)定點(diǎn)pivot。在快速排序遞歸過程中分成的子樹不能保證每次都是平均的將整個(gè)數(shù)組一分為二,換句話來說分成的子數(shù)組可能是一大一小的。
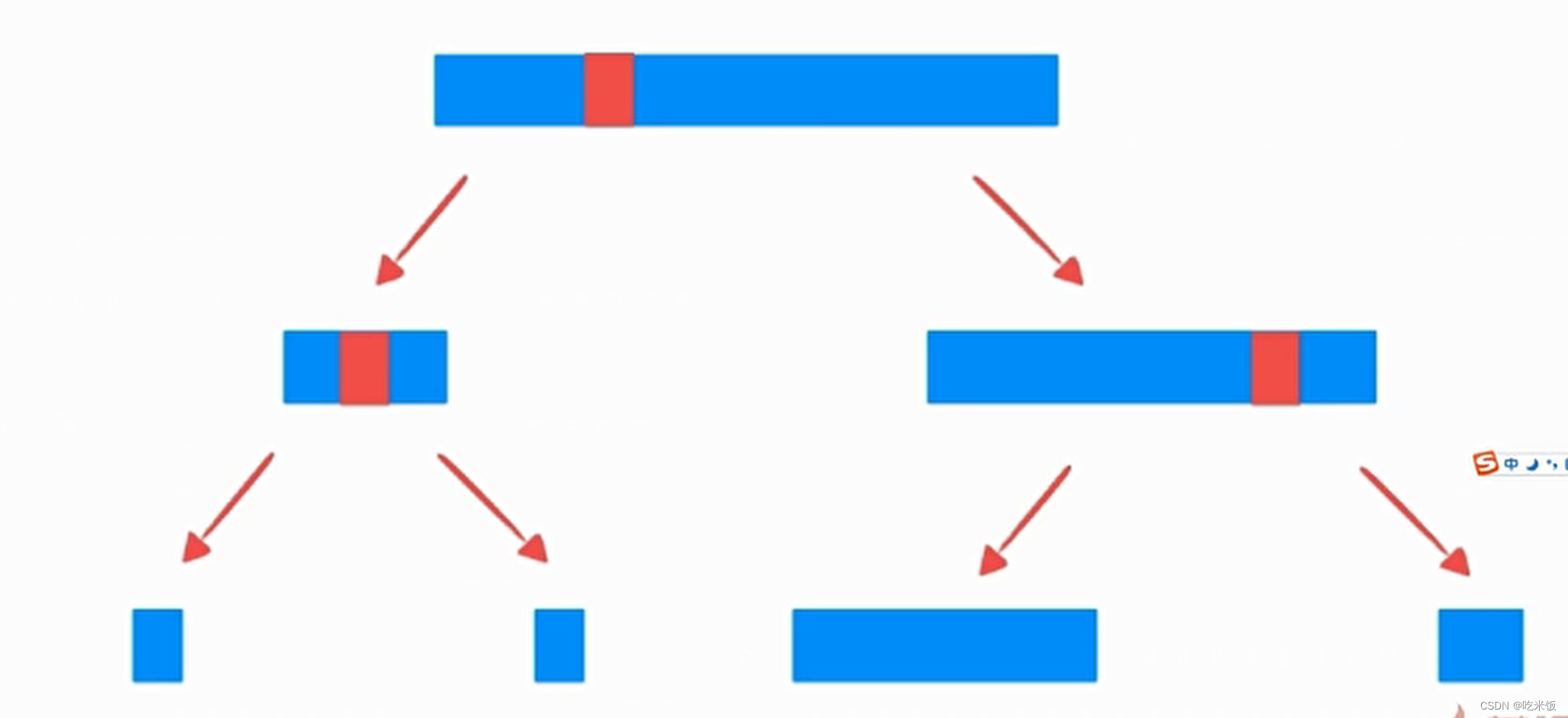
- 如果數(shù)組近乎或完全有序那么:
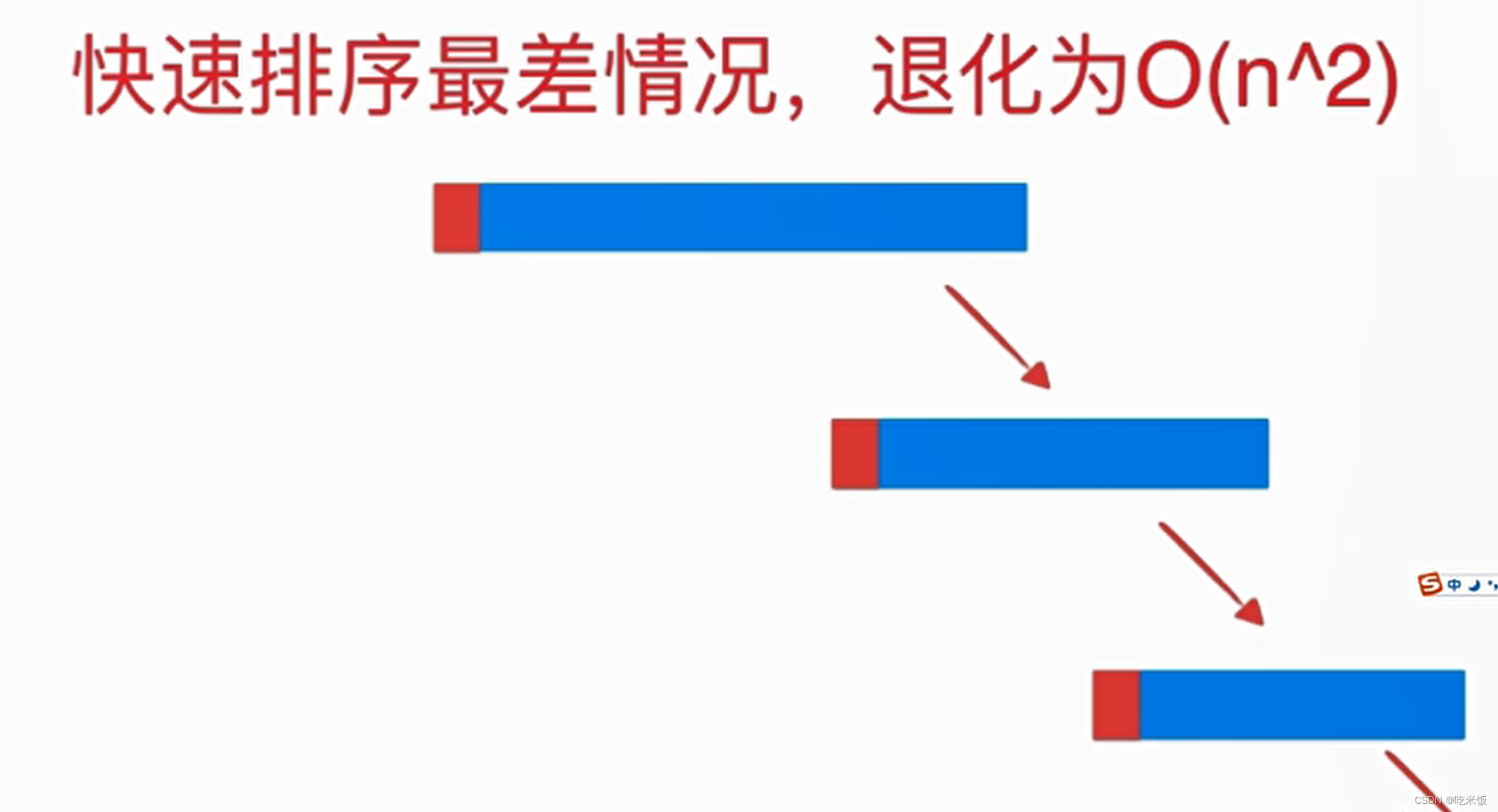
quickSort
// 對arr[l...r]范圍的數(shù)組進(jìn)行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
for (int i = l + 1; i <= r; ++i) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j - 1] > e; --j) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
// 對arr[l...r]部分進(jìn)行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template<typename T>
int __partition1(T arr[], const int l, const int r) {
// 優(yōu)化:隨機(jī)在arr[l...r]的范圍中, 選擇一個(gè)數(shù)值作為標(biāo)定點(diǎn)pivot
std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
const T v = arr[l];
int j = l;
// arr[l+1...j] < v ; arr[j+1...i) > v
for (int i = l + 1; i <= r; ++i) {
if (arr[i] < v) {
std::swap(arr[++j], arr[i]);
}
}
std::swap(arr[l], arr[j]);
return j;
}
// 對arr[l...r]部分進(jìn)行快速排序
template<typename T>
void __quickSort(T arr[], const int l, const int r) {
// 優(yōu)化:對于小規(guī)模數(shù)組, 使用插入排序進(jìn)行優(yōu)化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
const int p = __partition1(arr, l, r);
__quickSort(arr, l, p - 1);
__quickSort(arr, p + 1, r);
}
//快速排序
template<typename T>
void quickSort(T arr[], const int n) {
srand(time(NULL));
__quickSort(arr, 0, n - 1);
}
雙路快速排序
在之前的快速排序我們沒有討論在等于v的情況,在這里無論是把等于放在左邊還是右邊,如果整個(gè)數(shù)組出現(xiàn)大量重復(fù)的元素,那么它就會造成左右分成的數(shù)組極度不平衡從而使算法退化成O(n^2)。
現(xiàn)在呢我們將小于v和大于v放在數(shù)組的兩端。首先我們從i這個(gè)位置開始向后掃描,當(dāng)我們面對的元素仍然是小于v的時(shí)候我們繼續(xù)向后掃描,知道我們碰到了元素e,它是大于等于v的。
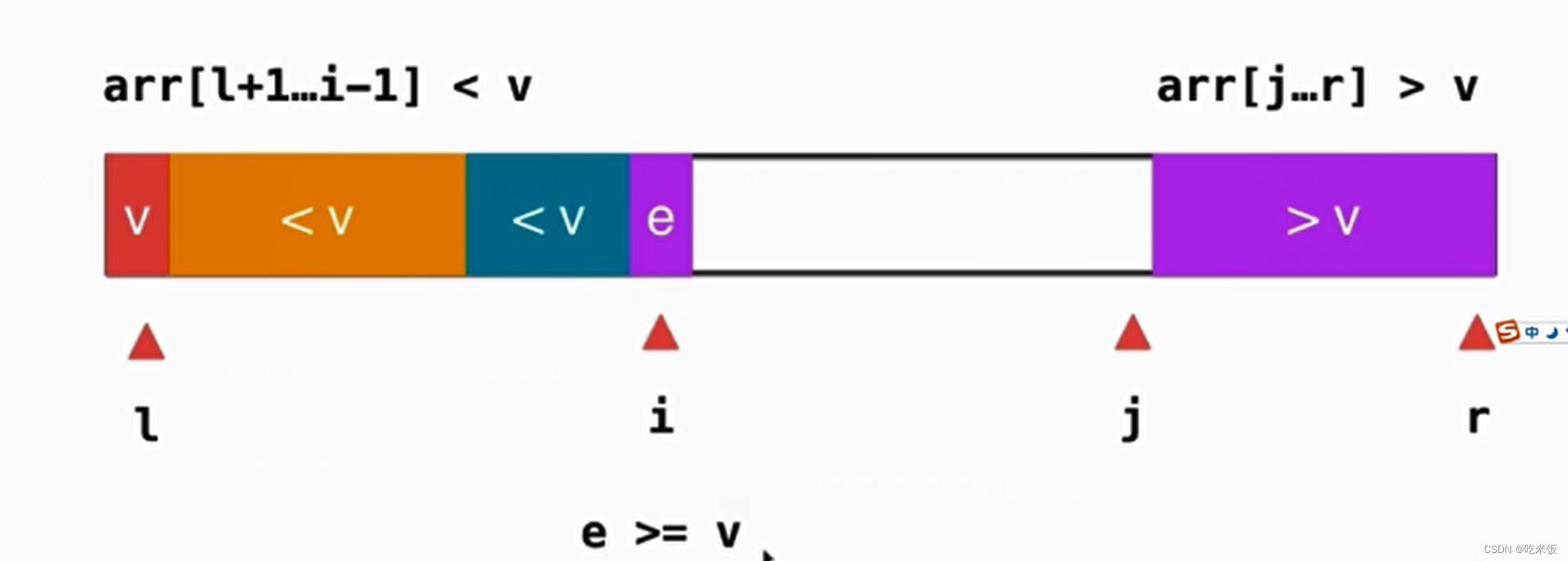
同樣 j 亦是如此,
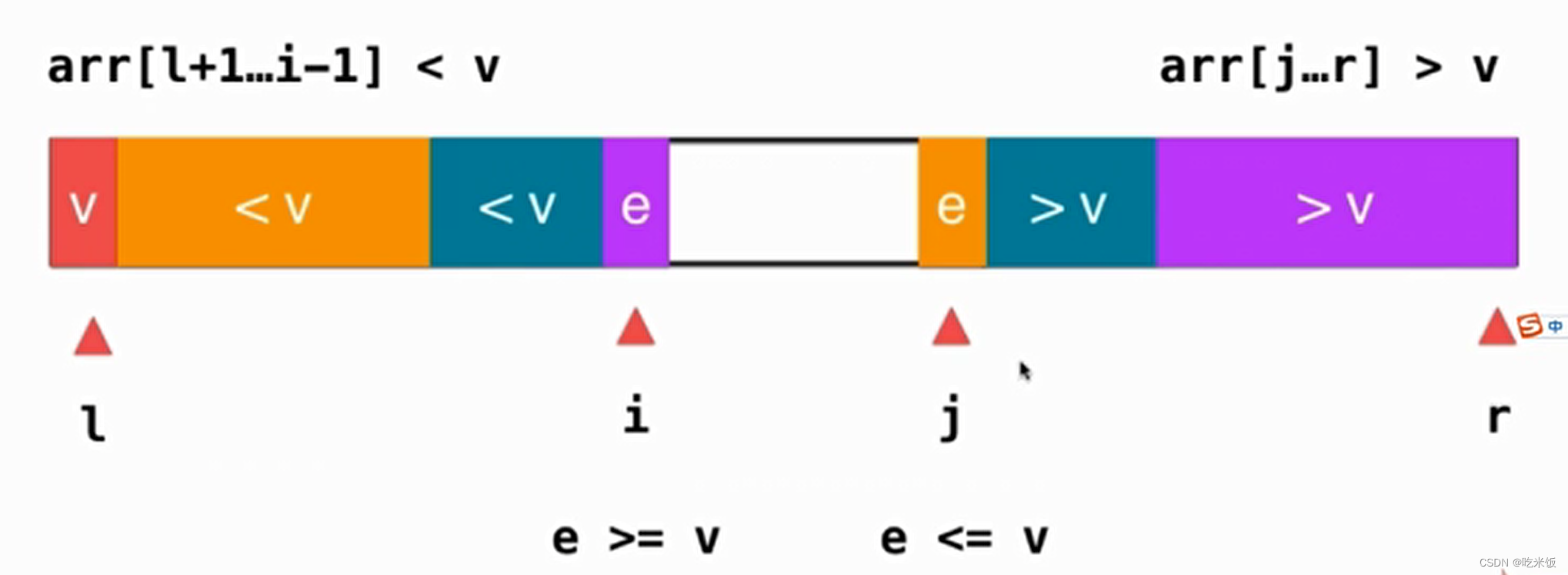
這樣話兩個(gè)綠色的部分就分別歸并到橙色和紫色。
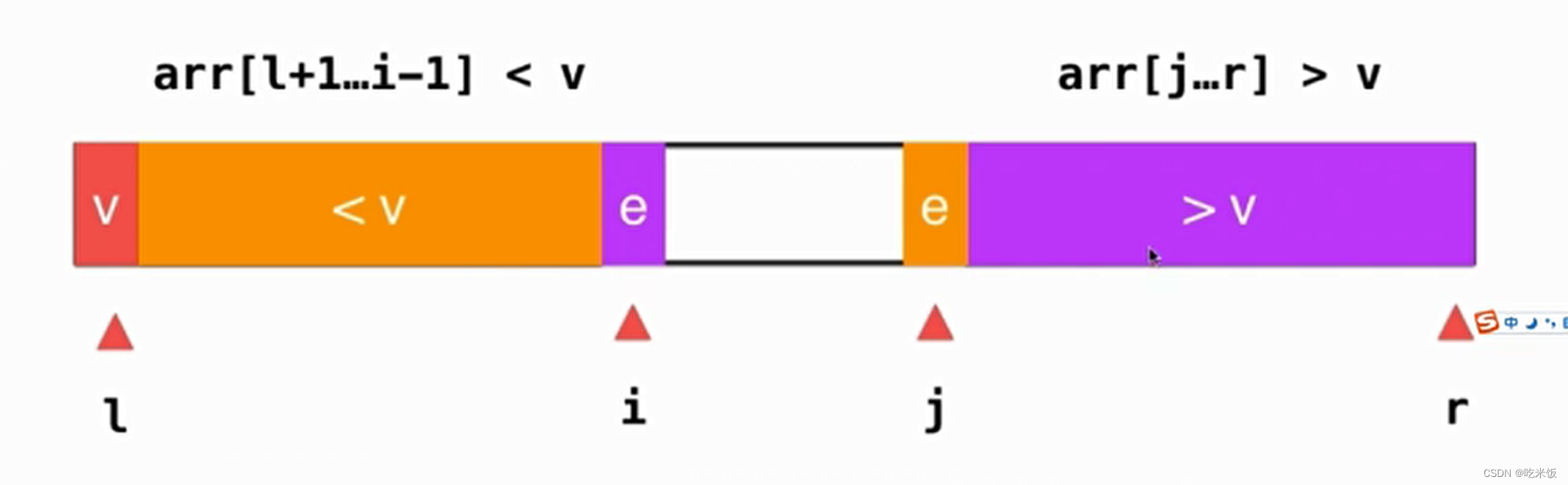
而 i和 j這兩個(gè)所指的元素交換一下位置就可以了。
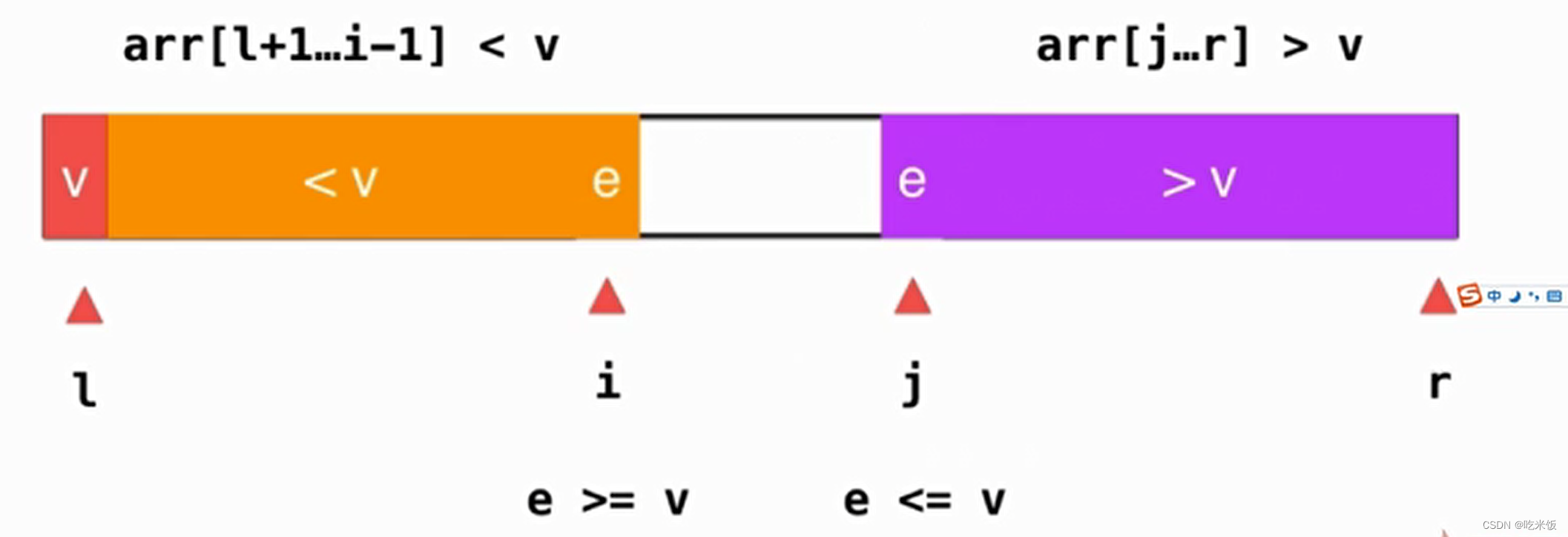
然后維護(hù)一下位置 ++i,--j,以此類推。
quickSort2Ways
// 對arr[l...r]范圍的數(shù)組進(jìn)行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
for (int i = l + 1; i <= r; ++i) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j - 1] > e; --j) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
// 雙路快速排序的partition
// 返回p, 使得arr[l...p-1] <= arr[p] ; arr[p+1...r] >= arr[p]
// 雙路快排處理的元素正好等于arr[p]的時(shí)候要注意,詳見下面的注釋:)
template<typename T>
int __partition2(T arr[], int l, int r) {
// 隨機(jī)在arr[l...r]的范圍中, 選擇一個(gè)數(shù)值作為標(biāo)定點(diǎn)pivot
std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
const T v = arr[l];
// arr[l+1...i) <= v; arr(j...r] >= v
int i = l + 1, j = r;
while (true) {
// 注意這里的邊界, arr[i] < v, 不能是arr[i] <= v
// 思考一下為什么?
while (i <= r && arr[i] < v)++i;
// 注意這里的邊界, arr[j] > v, 不能是arr[j] >= v
// 思考一下為什么?
while (j >= l + 1 && arr[j] > v)--j;
if (i > j)break;
std::swap(arr[i], arr[j]);
//arr[i] < v. 在碰到很多連續(xù)相同數(shù)字的情況下,i只向后移動一次,同時(shí)j至少向前移動一次,相對平衡。
//arr[i] <= vb, 在碰到很多連續(xù)相同數(shù)字的情況下, i首先不停向后移動,直到滿足條件為止,造成不平衡。
++i;
--j;
}
std::swap(arr[l], arr[j]);
return j;
}
// 對arr[l...r]部分進(jìn)行快速排序
template<typename T>
void __quickSort2Ways(T arr[], const int l, const int r) {
// 對于小規(guī)模數(shù)組, 使用插入排序進(jìn)行優(yōu)化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
const int p = __partition2(arr, l, r);
__quickSort2Ways(arr, l, p - 1);
__quickSort2Ways(arr, p + 1, r);
}
//快速排序
template<typename T>
void quickSort2Ways(T arr[], const int n) {
srand(time(NULL));
__quickSort2Ways(arr, 0, n - 1);
}
三路快速排序
之前快速排序的思想都是小于v大于v,而三路快速排序的思想是小于v等于v大于v。在這樣分割之后在遞歸的過程中,對于等于v的我們根本不用管了,只需要遞歸小于v大于v的部分進(jìn)行同樣的快速排序。
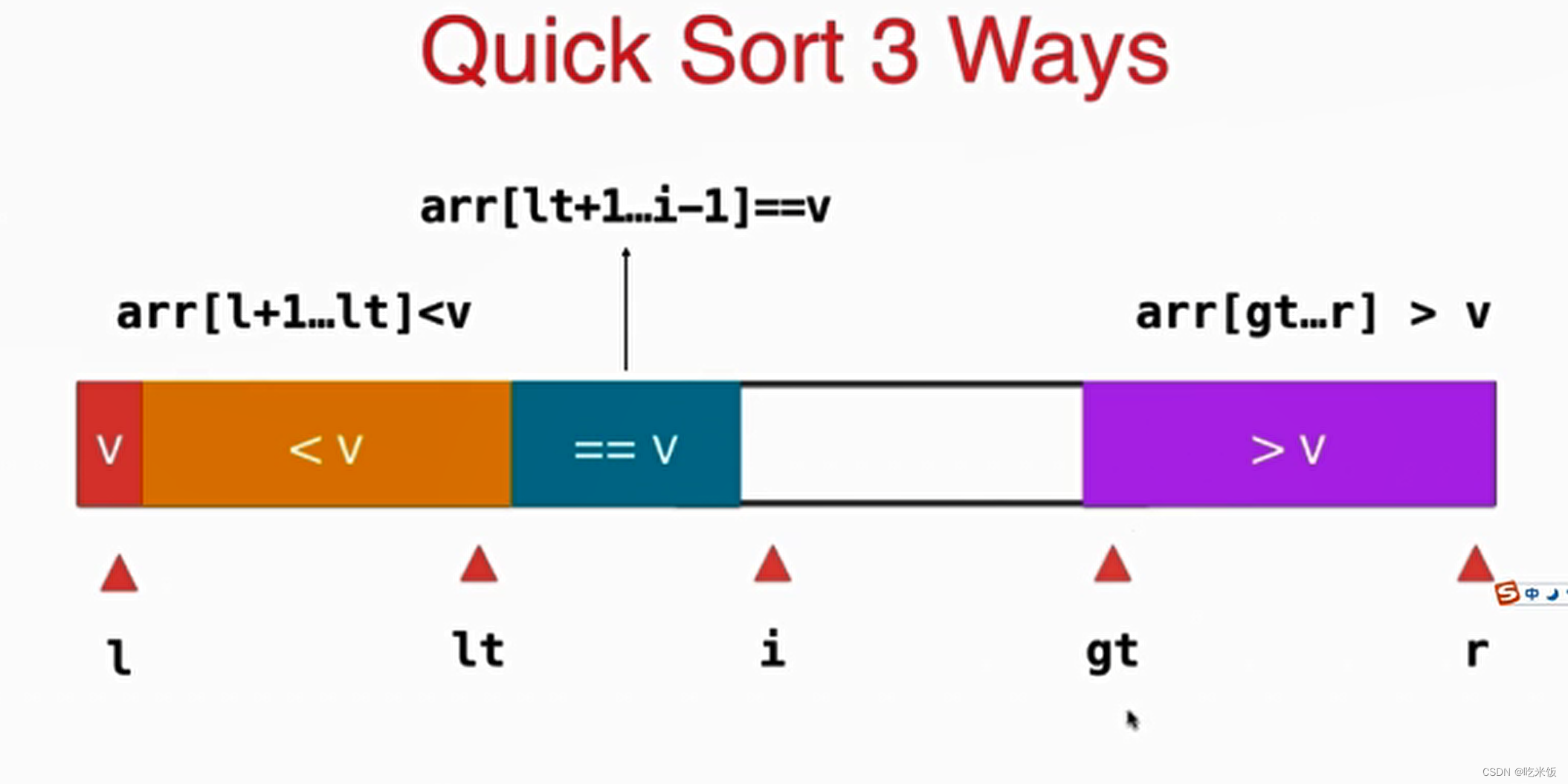
現(xiàn)在我們要處理i位置這個(gè)元素e,如果當(dāng)前元素 e 正好等于v,那么元素e就直接納入綠色的等于v的部分,相應(yīng)的 ++i,我們來處理下一位置的元素。
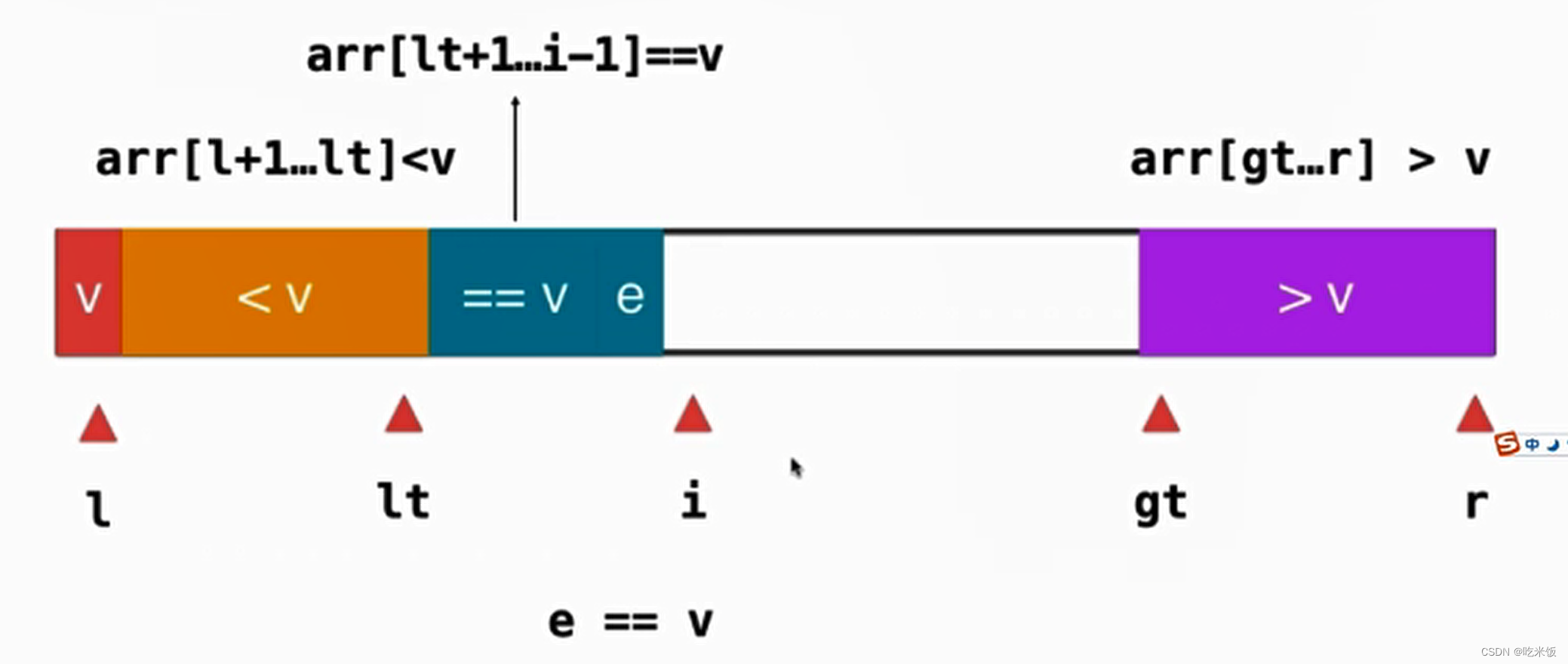
如果當(dāng)前元素 e 小于v,我們只需要把這個(gè)元素和等于v部分的第一個(gè)元素進(jìn)行一次交換就好了。
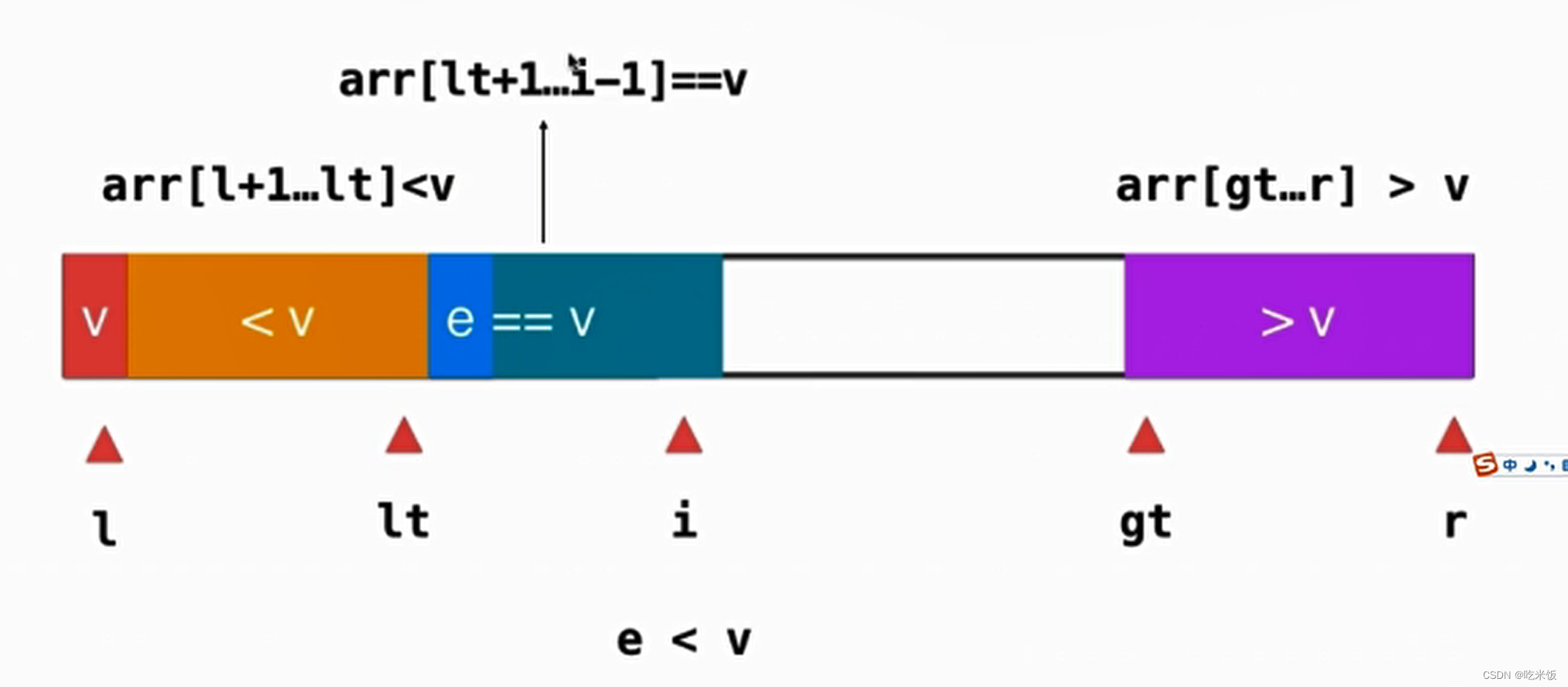
之后因該維護(hù)一下位置,++i,++lt,來查看下一元素。
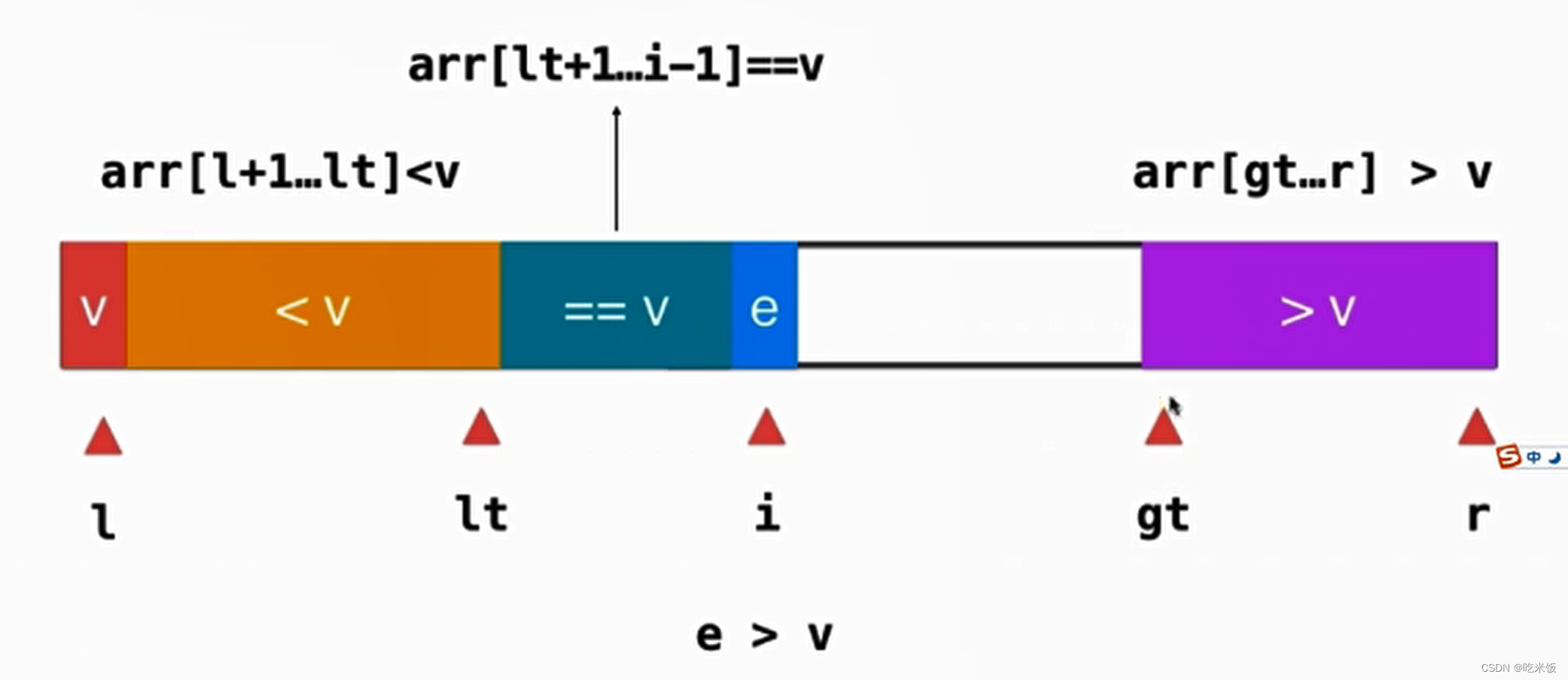
如果當(dāng)前元素 e 大于v,我們只需要把這個(gè)元素和gt-1位置的元素進(jìn)行一次交換就好了。
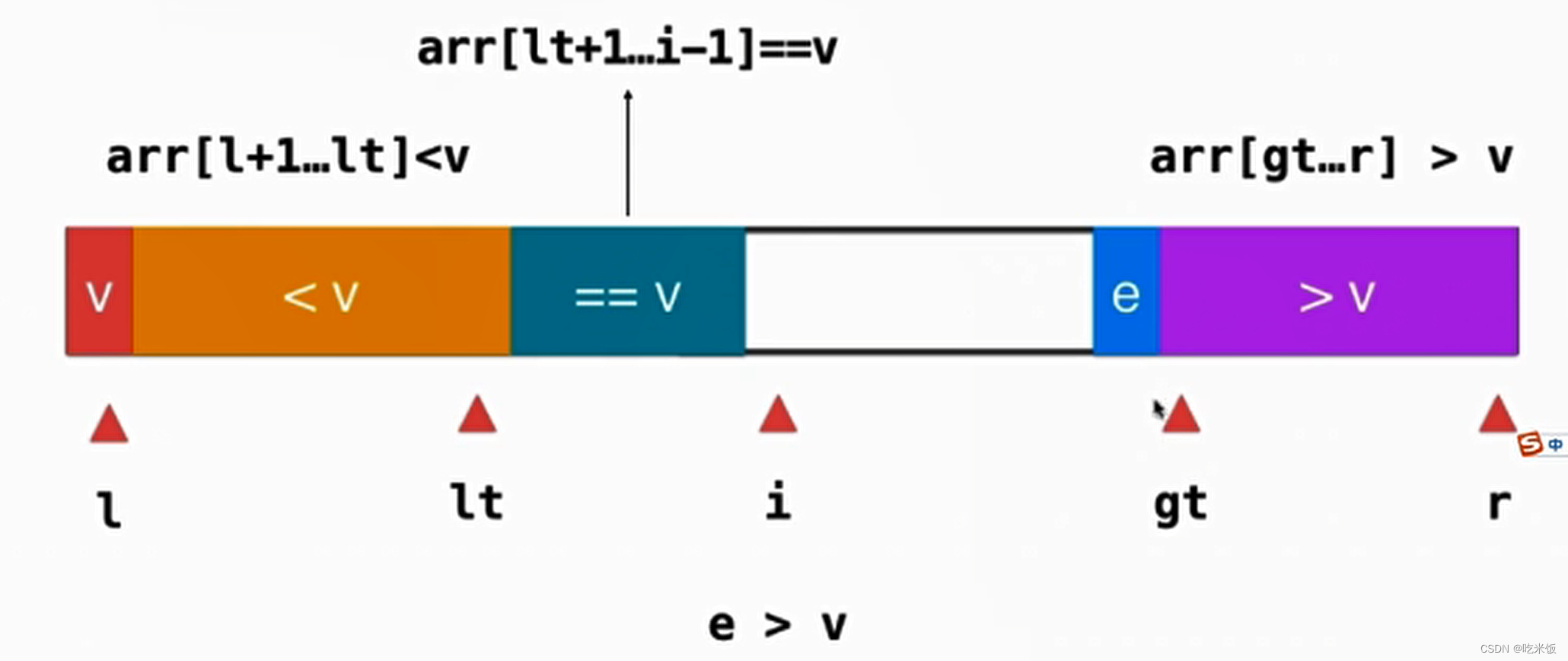
相應(yīng)的我們應(yīng)該維護(hù)一下gt的位置 --gt,需要注意的是i我們不需要?jiǎng)铀驗(yàn)楹退粨Q的位置元素本就沒有討論過。
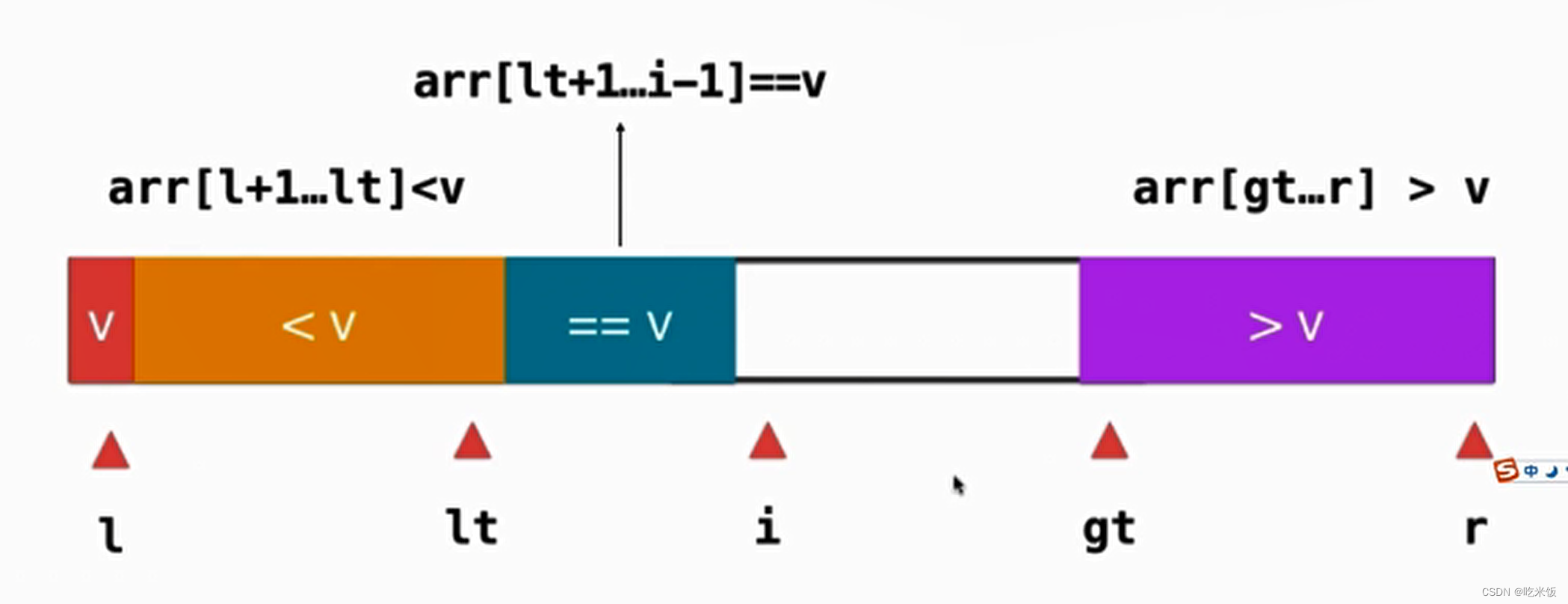
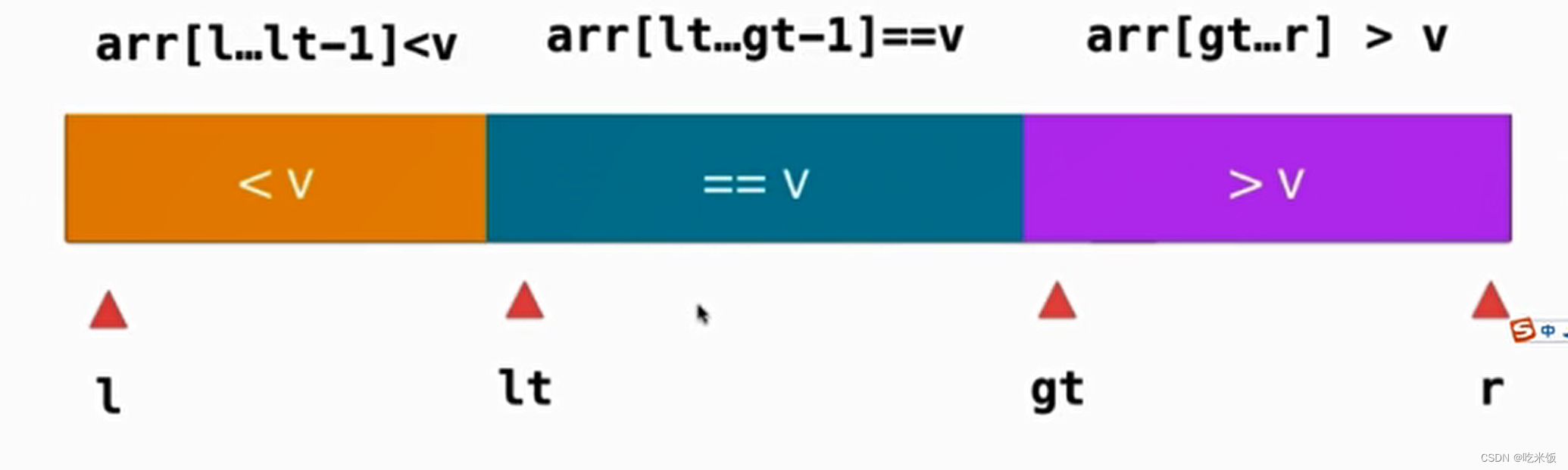
以此類推,最后還需要l和lt位置的元素交換一下位置。

此時(shí)我們整個(gè)數(shù)組就變成了這個(gè)樣子,之后我們只需要對小于v的部分和大于v的部分進(jìn)行遞歸的快速排序就好了,至于等于v的部分它已經(jīng)放在數(shù)組合適的位置了。
quickSort3Ways
// 對arr[l...r]范圍的數(shù)組進(jìn)行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
for (int i = l + 1; i <= r; ++i) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j - 1] > e; --j) {
arr[j] = arr[j - 1];
}
arr[j] = e;
}
}
// 遞歸的三路快速排序算法
template<typename T>
void __quickSort3Ways(T arr[], const int l, const int r) {
// 對于小規(guī)模數(shù)組, 使用插入排序進(jìn)行優(yōu)化
if (r - l <= 15) {
insertionSort(arr, l, r);
return;
}
// 隨機(jī)在arr[l...r]的范圍中, 選擇一個(gè)數(shù)值作為標(biāo)定點(diǎn)pivot
std::swap(arr[l], arr[rand() % (r - l + 1) + l]);
T v = arr[l];
int lt = l; // arr[l+1...lt] < v
int gt = r + 1; // arr[gt...r] > v
int i = l + 1; // arr[lt+1...i) == v
while (i < gt) {
if (arr[i] < v) {
std::swap(arr[i], arr[lt + 1]);
++i;
++lt;
} else if (arr[i] > v) {
std::swap(arr[i], arr[gt - 1]);
--gt;
} else { // arr[i] == v
++i;
}
}
std::swap(arr[l], arr[lt]);
__quickSort3Ways(arr, l, lt - 1);
__quickSort3Ways(arr, gt, r);
}
// 對于包含有大量重復(fù)數(shù)據(jù)的數(shù)組, 三路快排有巨大的優(yōu)勢
template<typename T>
void quickSort3Ways(T arr[], const int n) {
srand(time(nullptr));
__quickSort3Ways(arr, 0, n - 1);
}
概述




 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號