歸并排序

首先把數組分成一半，想辦法把左右兩邊數組排序，之后呢再將它們歸并起來，這就是歸并排序的基本思想。

這樣的話如果有N個元素，就會分成log(n)層，如果整個歸并過程我們可以以O(n)時間復雜度解決的話，那么我們就設計成了一個 Nlog(n)級別的排序算法。




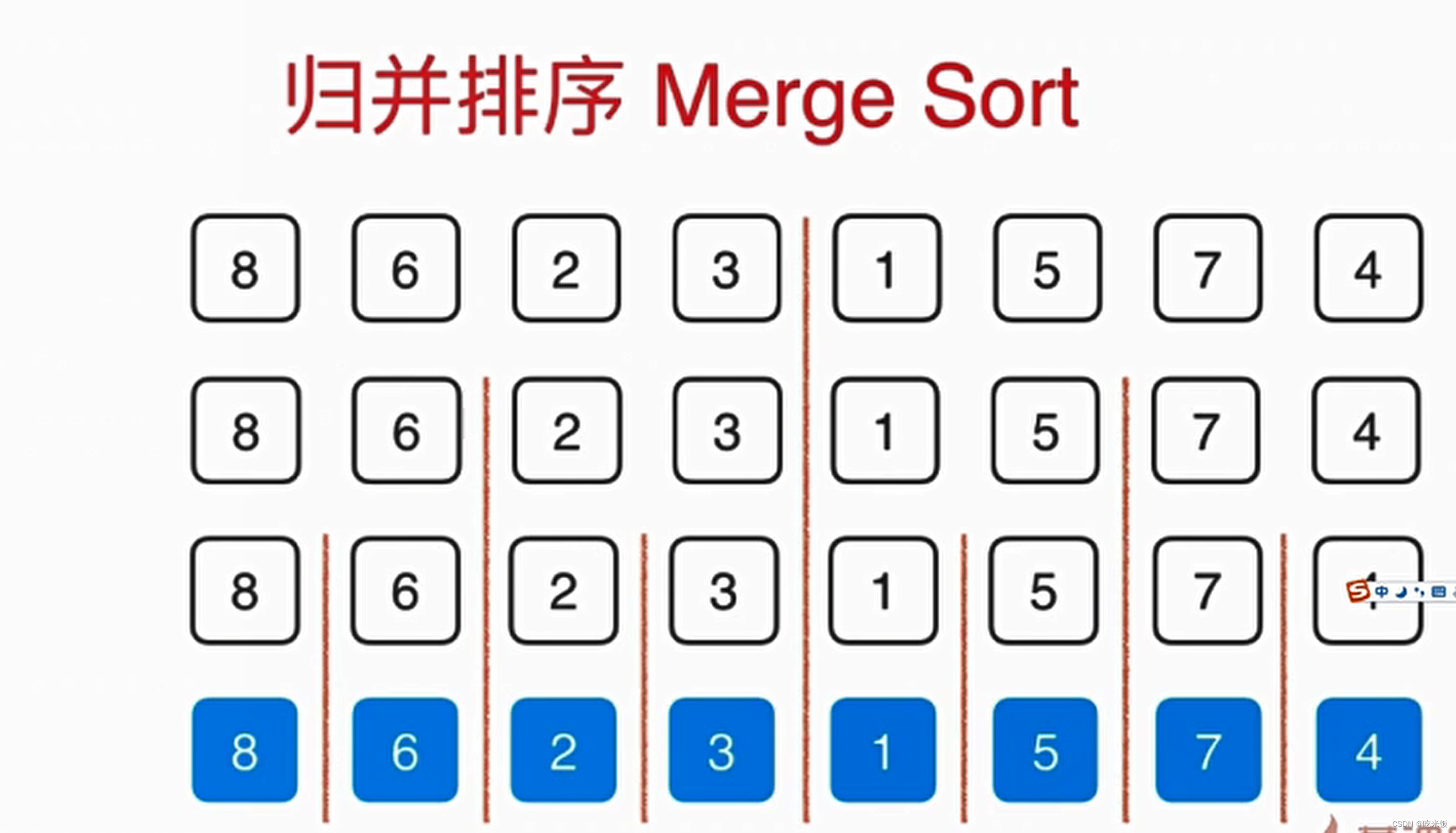
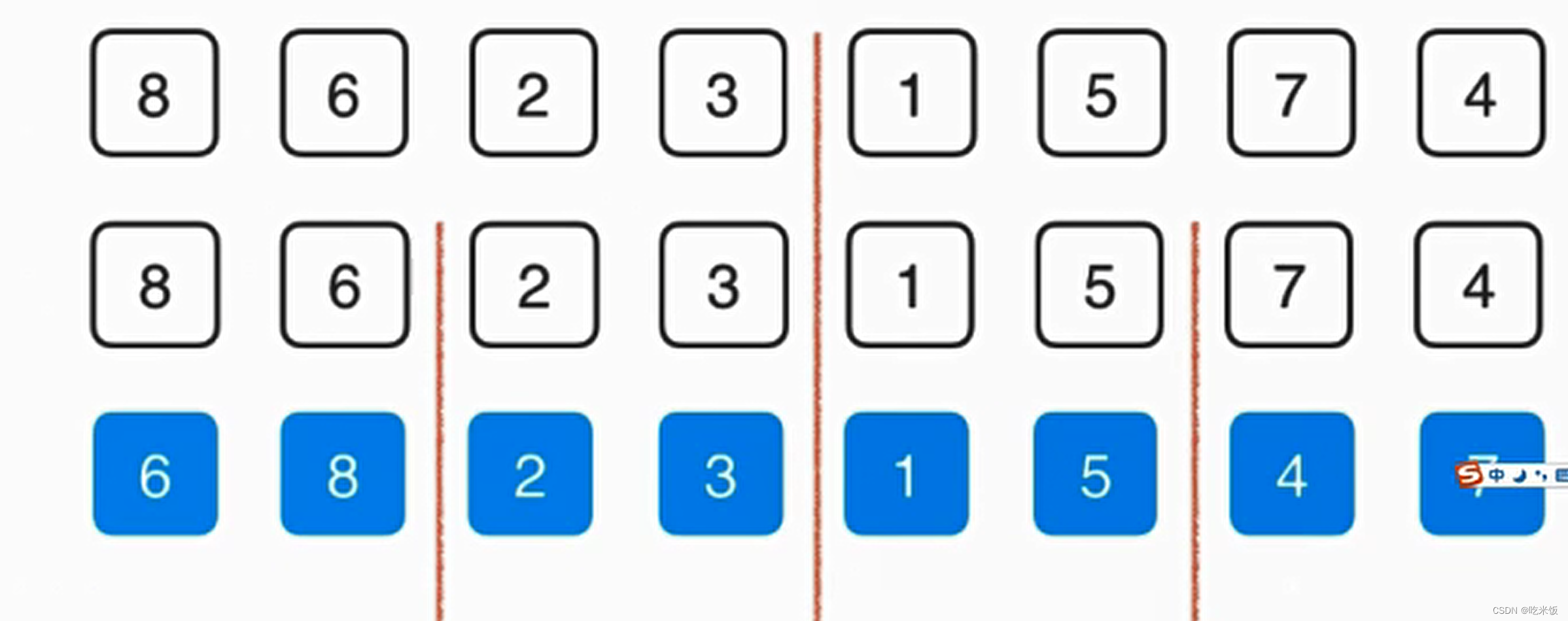
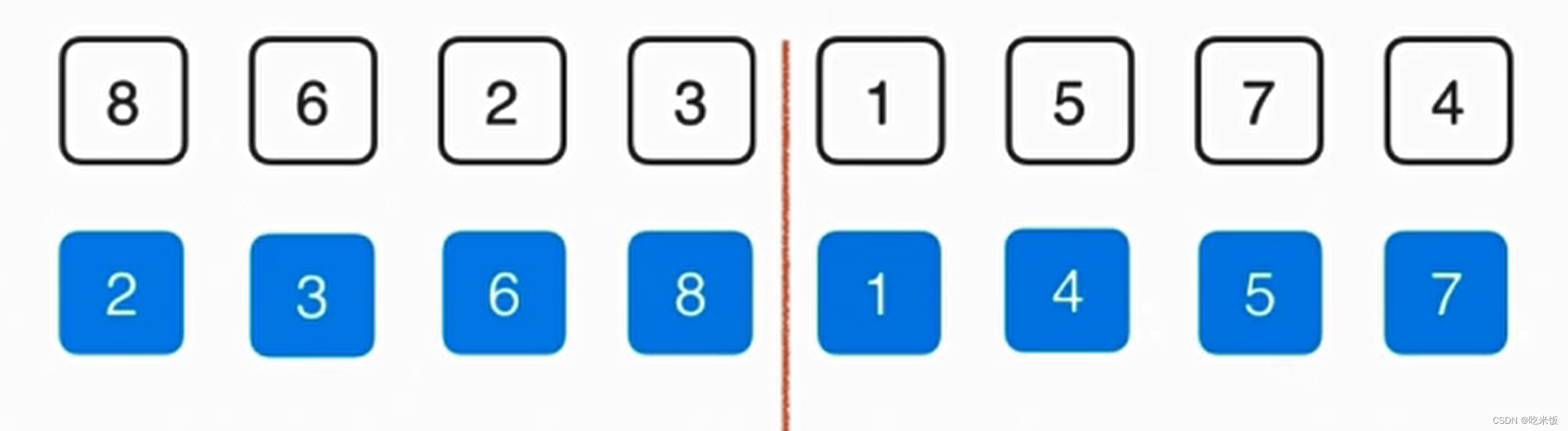
這個歸并的過程需要O(n)的輔助空間，把兩個已經排好序的數組合并成一個排序數組，整體呢需要三個索引在數組中追蹤，其中藍色的箭頭表示最終在歸并的過程中我們需要跟蹤的位置，而倆個紅色的箭頭表示當前已經排好序的數組，分別指向當前要考慮的元素。

首先我們要看1和2誰先放在最終數組中，顯然1比2小所以我們首先把1放在最終數組中，這樣藍色箭頭就可以考慮下一元素應該放誰，與此同時，下面紅色箭頭1所在數組也可以考慮下一元素了，此時1這個元素就最終有序了，然后我們就可以考慮2和4誰放入最終數組，顯然是2，以此類推。

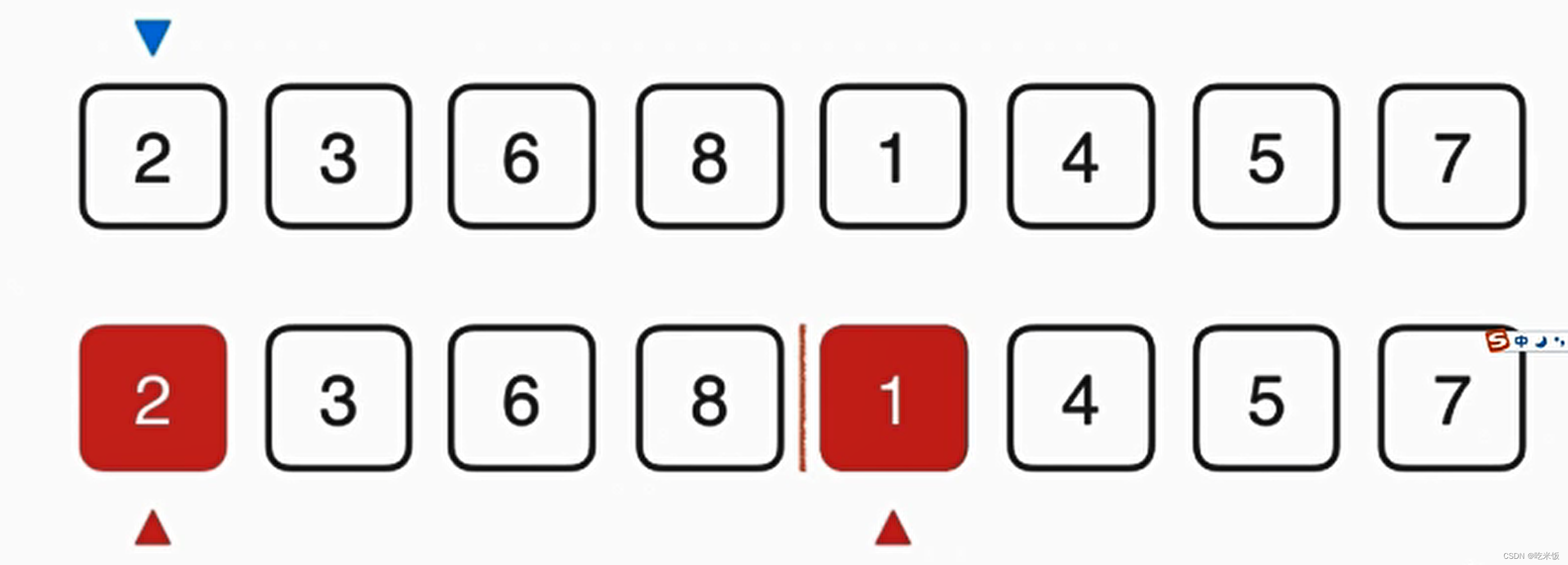
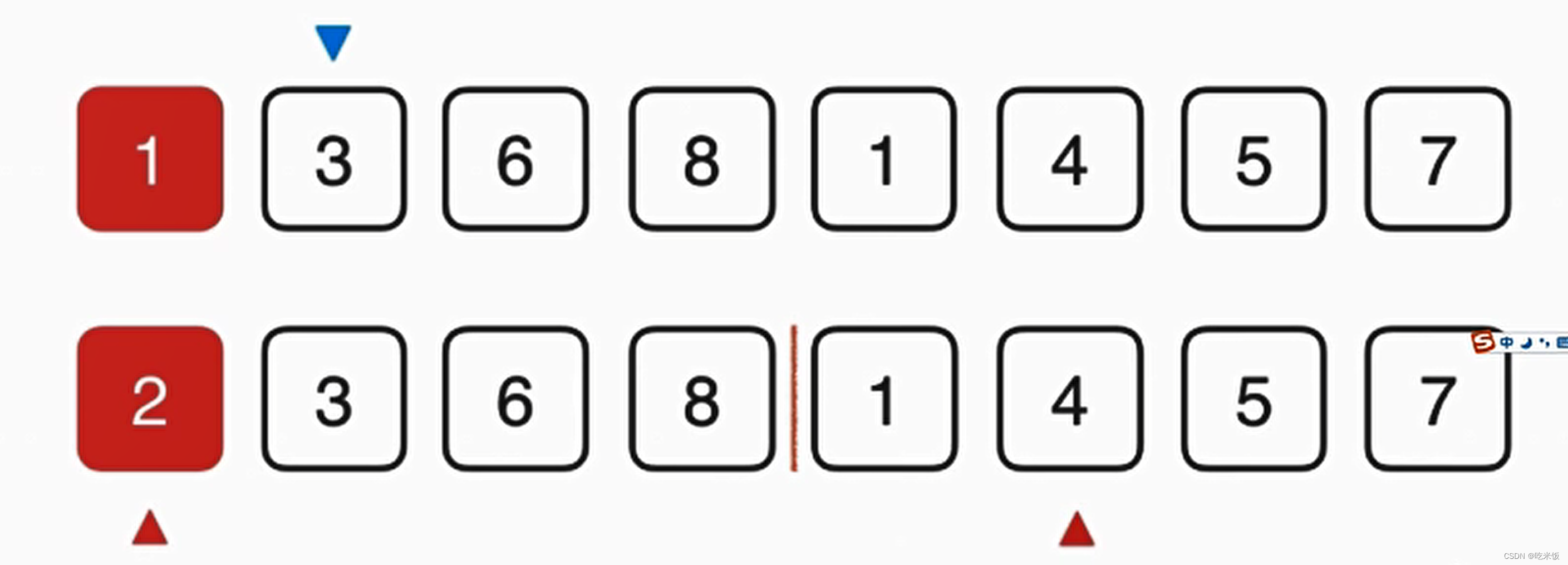
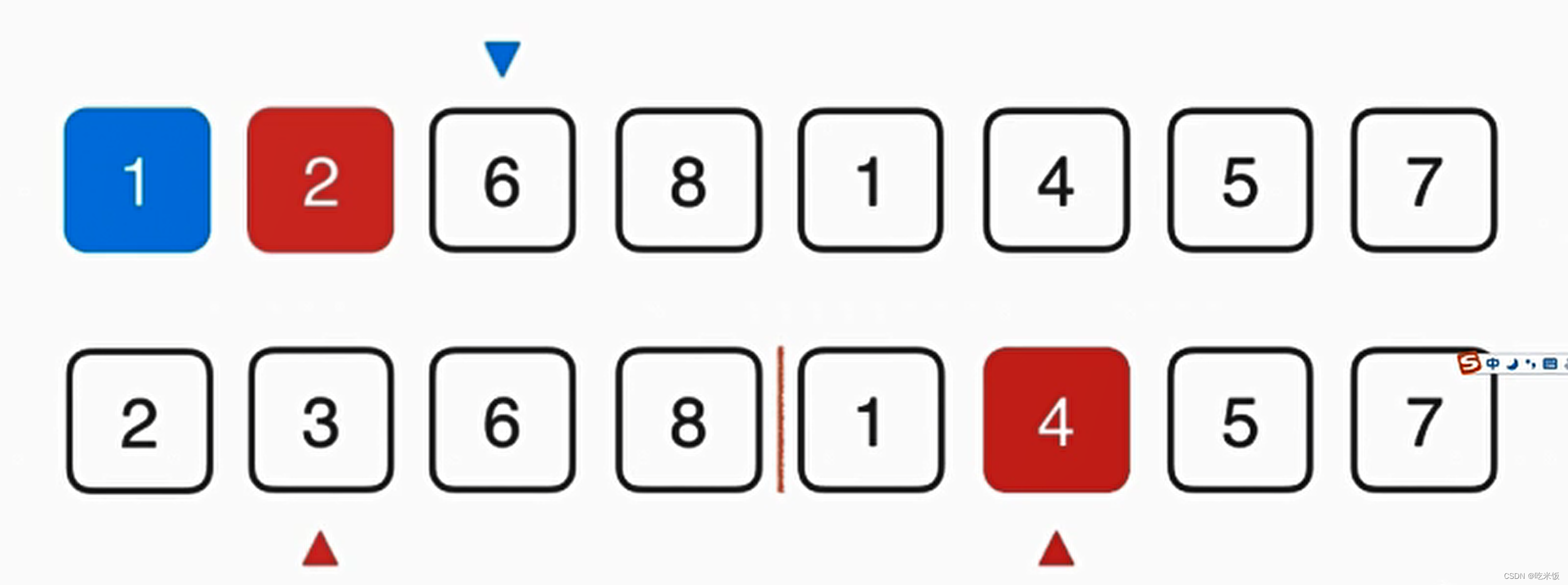
對于這些索引位置定義

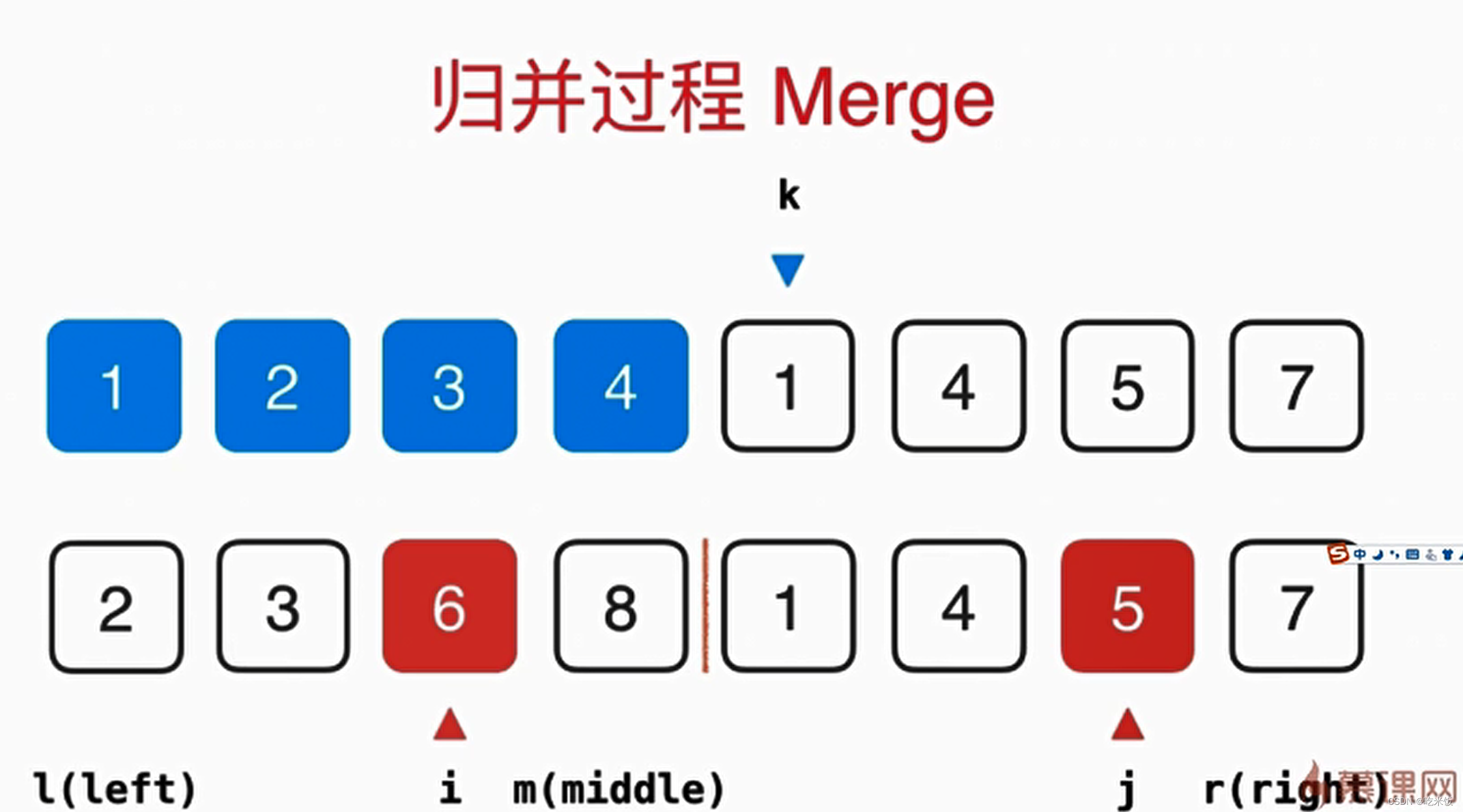
優化

• 對于arr[mid] <= arr[mid+1]的情況相當于整個arr就是有序,不進行merge
• 對于小規模數組近乎有序的概率比較大, 使用插入排序有優勢

mergeSort

// 對arr[l...r]范圍的數組進行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r) {
   for (int i = l + 1; i <= r; i++) {
       T e = arr[i];
       int j;
       for (j = i; j > l && arr[j - 1] > e; j--) {
           arr[j] = arr[j - 1];
       }
       arr[j] = e;
   }
}

// 將arr[l...mid]和arr[mid+1...r]兩部分進行歸并
template<typename T>
void __merge(T arr[], const int l, const int mid, const int r) {
   T aux[r - l + 1];
   for (int i = l; i <= r; ++i) {
       aux[i - l] = arr[i];
   }
   // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
   int i = l, j = mid + 1;
   for (int k = l; k <= r; ++k) {
       if (i > mid) {  // 如果左半部分元素已經全部處理完畢
           arr[k] = aux[j - l];
           ++j;
       } else if (j > r) {  // 如果右半部分元素已經全部處理完畢
           arr[k] = aux[i - l];
           ++i;
       } else if (aux[i - l] < aux[j - l]) {  // 左半部分所指元素 < 右半部分所指元素
           arr[k] = aux[i - l];
           ++i;
       } else {  // 左半部分所指元素 >= 右半部分所指元素
           arr[k] = aux[j - l];
           ++j;
       }
   }
}

// 遞歸使用歸并排序,對arr[l...r]的范圍進行排序
template<typename T>
void __mergeSort(T arr[], const int l, const int r) {
   /*if (l >= r) {
       return;
   }*/
   // 優化2: 對于小規模數組近乎有序的概率比較大, 使用插入排序有優勢
   if (r - l <= 15) {
       insertionSort(arr, l, r);
       return;
   }
   int mid = l + (r - l) / 2;
   __mergeSort(arr, l, mid);
   __mergeSort(arr, mid + 1, r);
   // 優化1: 對于arr[mid] <= arr[mid+1]的情況相當于整個arr就是有序,不進行merge
   // 對于近乎有序的數組非常有效,但是對于一般情況,有一定的性能損失
   if (arr[mid] > arr[mid + 1]) {
       __merge(arr, l, mid, r);
   }
}

//歸并排序
template<typename T>
void mergeSort(T arr[], const int n) {
   __mergeSort(arr, 0, n - 1);
}

自底向上歸并排序

使用自底向上的歸并排序算法 Merge Sort BU 也是一個O(nlogn)復雜度的算法，雖然只使用兩重for循環，但是，Merge Sort BU也可以在1秒之內輕松處理100萬數量級的數據，需要注意的是：不要輕易根據循環層數來判斷算法的復雜度，Merge Sort BU就是一個反例。

比較Merge Sort和Merge Sort Bottom Up兩種排序算法的性能效率，整體而言, 兩種算法的效率是差不多的。但是如果進行仔細測試，從統計意義上來講自頂向下的歸并排序會略勝一籌。不過Merge Sort Bottom Up 有一個非常重要的作用，這個代碼中沒有使用數組的索引獲取元素特性，就因如此可以非常好的在nlog(n)的時間對鏈表這樣的數據結構進行排序。

template<typename T>
void mergeSortBU(T arr[], const int n) {
    // Merge Sort Bottom Up 優化
    // 對于小數組, 使用插入排序優化
    for (int i = 0; i < n; i += 16) {
        insertionSort(arr, i, std::min(i + 15, n - 1));
    }
    for (int sz = 16; sz < n; sz += sz) {
        for (int i = 0; i < n - sz; i += sz + sz) {
            // 對于arr[mid] <= arr[mid+1]的情況,不進行merge
            if (arr[i + sz - 1] > arr[i + sz]) {
                __merge(arr, i, i + sz - 1, std::min(i + sz + sz - 1, n - 1));
            }
        }
    }
}

概述