test26

我當逐明月枕清風qingfeng

區間加減先改成在差分數組上選擇 \(i,j\in [1,n+1],i\neq j\) 使得 \(d_i\gets d_{i}+1,d_j\gets d_{j}-1\)，目標就是讓 \(d_{2\to n}=0\)，所以考慮讓函數 \(f(d)=\sum_{i=2}^n |d_i|\) 下降到 \(0\)。首先如果 \(i,j\in [2,n]\) 且 \(d_id_j<0\)，會使 \(f\) 下降 2，這是最優的，在存在這樣的合法對時一定會用這種。然后就是 \(\forall d_{2\to n}\geq 0\) 或者反之的情況了，可以選擇向 \(d_1/d_{n+1}\) 傳遞貢獻，讓 \(f\) 下降 \(1\)，設 \(L=\sum_{i=2}^n[d_i>0]d_i,R=\sum_{i=2}^n [d_i<0]|d_i|\)，那么操作次數一定是 \(max(L,R)\)，還沒有嚴謹闡述的正確性都可以對著 \(f\) 捏出來，注意到讓 \(f\) 降 \(1\) 的貢獻可以選擇放左/右 \(x,|L-R|-x\) 次這種對，所以序列數就是 \(|L-R|+1\)。

#include<bits/stdc++.h>
#define int long long
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)

using namespace std;

const int N=100005;

int n, a[N], L, R;

signed main() {
	freopen("qingfeng.in","r",stdin);
	freopen("qingfeng.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;
	up(i,1,n) cin >> a[i];
	dn(i,n,1) a[i]-=a[i-1];
	up(i,2,n) if(a[i]<0) L-=a[i]; else R+=a[i];
	cout << max(L,R) << '\n' << abs(L-R)+1 << '\n';
	return 0;
}

一身坦蕩明晃晃魑魍魎wangliang

首先這個是有向圖，其次這個不是 dag，所以最長路不行，那我們只能考慮建圖縮點然后 dfs，建圖的話對需要的行或者列建立一個輔助點即可。

#include<bits/stdc++.h>
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)
#define pii pair<int,int>
#define mp make_pair
#define pb push_back

using namespace std;

const int N=300005;
const int dx[9]={0,1,-1,0,0,1,1,-1,-1};
const int dy[9]={0,0,0,1,-1,1,-1,1,-1};

int n, m, R, C, x[N], y[N], opt[N];
int stk[N], top, gp[N], vis[N], cnt, p, val[N], Ans;
vector<int> F[N], G[N], to[N];
map<int,int> idx, idy;
map<pii,int> qwq;

inline void eadd(int u,int v) {
	F[u].pb(v), G[v].pb(u);
}

void dfs(int x) {
	vis[x]=1;
	for(int y:F[x]) if(!vis[y]) dfs(y);
	stk[++top]=x;
}

void stain(int x) {
	for(int y:G[x]) if(!gp[y]) gp[y]=cnt, stain(y);
}

void Dfs(int x) {
	vis[x]=val[x];
	for(int y:to[x]) {
		if(!vis[y]) Dfs(y);
		vis[x]=max(vis[x],vis[y]+val[x]);
	}
	Ans=max(Ans,vis[x]);
}

signed main() {
	freopen("wangliang.in","r",stdin);
	freopen("wangliang.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n >> R >> C, m=n;
	up(i,1,n) {
		cin >> x[i] >> y[i] >> opt[i];
		if(opt[i]==1&&!idx[x[i]]) idx[x[i]]=++m;
		if(opt[i]==2&&!idy[y[i]]) idy[y[i]]=++m; 
		qwq[mp(x[i],y[i])]=i;
	}
	up(i,1,n) {
		if(idx.find(x[i])!=idx.end()) eadd(idx[x[i]],i);
		if(idy.find(y[i])!=idy.end()) eadd(idy[y[i]],i);
		if(opt[i]==1) eadd(i,idx[x[i]]);
		if(opt[i]==2) eadd(i,idy[y[i]]);
		if(opt[i]==3) {
			up(o,1,8) {
				int xx=x[i]+dx[o], yy=y[i]+dy[o];
				if(qwq.find(mp(xx,yy))!=qwq.end()) {
					int j=qwq[mp(xx,yy)];
					eadd(i,j);
				}
			} 
		}
	}
	up(i,1,m) if(!vis[i]) dfs(i);
	dn(i,m,1) if(!gp[p=stk[i]]) gp[p]=++cnt, stain(p);
	up(i,1,n) ++val[gp[i]]; 
	up(i,1,m) for(int j:F[i]) if(gp[i]!=gp[j]) to[gp[i]].pb(gp[j]);
	up(i,1,m) vis[i]=0;
	up(i,1,n) if(!vis[gp[i]]) Dfs(gp[i]);
	cout << Ans << '\n';
	return 0;
}

我當工有所償學有所用suoyong

題目要求“自覺強制在線”，注意到分塊也可以強制在線，那么寫分塊，但是不自覺地提前計算了 \(n=\sum |s_i|\) 來計算 \(B\) ，然后懶得取 \(\max\{len_i\}\) 用其預處理了哈希，然后就 RE 了，這是什么新型檢驗自覺性的方式嘛（？

其實我已經不太記得 ac 自動機怎么寫了，但是這個一看就能根號分治不是嗎。 \(len>B\) 的加入對 \(len\leq B\) 的查詢沒有貢獻，\(len\leq B\) 的加入可以塞進哈希表、查詢的時候考慮所有的左右端點的情況在哈希里面查數量，\(len>B\) 的插入對 \(len>B\) 的查詢可以暴力做。

#include<bits/stdc++.h>
#define ull unsigned long long
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)
#define pb push_back

using namespace std;

const int N=3000005;
const ull base=233;

int n, m, B, opt[N], len[N], g[N];
string str[N]; ull pw[N]; 
vector<int> diff; 
vector<ull> hsh[N];
unordered_map<ull,int> counter;

int sub(int b,int a) { // 在 str[b] 里面找 str[a] 
	int m=len[b], n=len[a], ret=0, j=0;
	up(i,2,n) {
		while(j&&str[a][j+1]!=str[a][i]) j=g[j];
		j+=(str[a][j+1]==str[a][i]), g[i]=j;
	}
	j=0;
	up(i,1,m) {
		while(j&&(str[a][j+1]!=str[b][i]||j==n)) j=g[j];
		j+=(str[a][j+1]==str[b][i]);
		if(j==n) ++ret;
	}
	return ret;
}

signed main() {
	freopen("suoyong.in","r",stdin);
	freopen("suoyong.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> m;
	up(i,1,m) {
		cin >> opt[i] >> str[i];
		n+=(len[i]=str[i].size());
		str[i]=" "+str[i]+" ";
		hsh[i].resize(len[i]+1);
		up(j,1,len[i]) hsh[i][j]=hsh[i][j-1]*base+(str[i][j]-'a'+1);
	}
	B=sqrt(n), pw[0]=1;
	up(i,1,n) pw[i]=pw[i-1]*base; 
	up(i,1,m) {
		if(opt[i]==3) {
			int Ans=0;
			up(j,1,len[i]) up(k,1,min(j,B)) {
				ull val=hsh[i][j]-hsh[i][j-k]*pw[k];
				if(counter.find(val)!=counter.end()) Ans+=counter[val];
			}
			if(len[i]>B) for(int j:diff) Ans+=sub(i,j);
			cout << Ans << '\n';
		}
		else {
			int val=opt[i]==1?1:-1;
			if(len[i]<=B) counter[hsh[i][len[i]]]+=val;
			else diff.pb(i);
		}
	}
	return 0;
}

無人笑我不自量ziliang

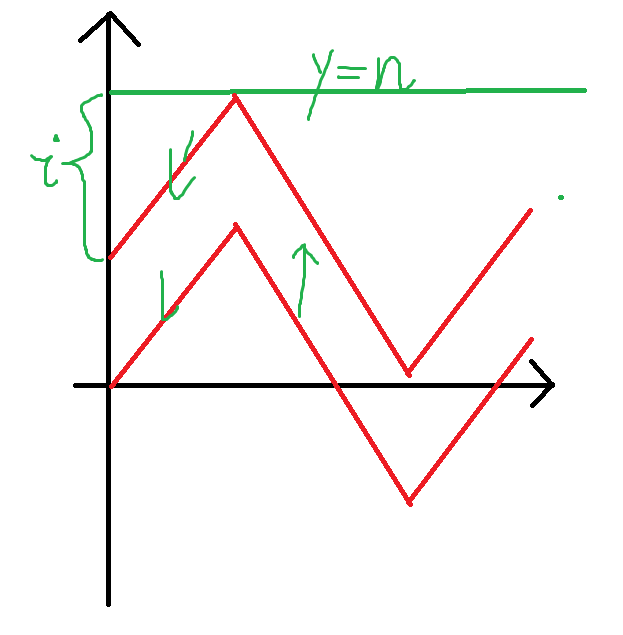
dp 算的東西是折線，關心的有 現在時間/現在高度/歷史最大高度，直接記這么多狀態不太實際喵，考慮怎么優化掉歷史最大高度，不妨把折線向上平移到切著 \(y=n\)，截距 \(i\) 就是最大值是 \(n-i\) 的意思，好像有點能歸到一起處理的意思了。要算期望我們希望令 \(f_{0,n-i}=h_i\)，然后帶著概率往下暴力 dp，順手加一維 \(0/1\) 表示有沒有碰到 \(y=n\)，不妨認為 \(x/y-x\) 種方案往上走/往下走，計算總貢獻即可，注意到一種形態的折線在同一時刻只有一條會觸碰過頂端，這個的正確性可以保證。

計算的對象是 \((i,s_i)\) 的走勢也就是圖中的 \(l\)，我們關心 \(l\) 的橫向長度 \(i\)，當前縱向高度 \(s_i\)，以及縱向歷史最大高度 \(h\)，這個是三維的狀態我們想辦法優化掉一維。不妨將 \(l\) 平移到 \(l'\) 使得最高點在 \(y=n\) 上，這樣子好像不關心 \(h\) 的具體值了只關心有沒有碰到過越過 \(y=n\)。

設 \(f_{i,j,0/1}\) 表示序列長度為 \(i\)，\(y(i)=j\)，沒有/有碰到過 \(y=n\) 的期望，初始 \(f_{0,n-i,[i=0]}=h_i\)，轉移 \(f_{i-1,j,0/1}\times (\frac{x}{y}/\frac{y-x}{y})\to f_{i,j\pm 1,0/1}\)，最后同層 \(f_{i,n,0}\to f_{i,n,1}\)，一層的答案就是 \(\sum f_{i,j,1}\)。正確性在于一種形態的折線，同一時刻只會有一條碰到過頂端，所以不重復。

#include<bits/stdc++.h>
#define int long long
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)

using namespace std;

const int N=5005, P=1e9+7;

int ksm(int a,int b=P-2) {
	int ret=1;
	for( ; b; b>>=1) {
		if(b&1) ret=ret*a%P;
		a=a*a%P;
	}
	return ret;
}

int T, n, p[N], q[N], h[N], f[2][N<<1][2];

inline void add(int &a,int b) { a=(a+b)%P; }

void mian() {
	cin >> n;
	up(i,1,n) {
		int x, y;
		cin >> x >> y;
		p[i]=x, q[i]=y-x;
	}
	up(i,0,n) cin >> h[i];
	up(i,-n,n) f[0][i+n][0]=f[0][i+n][1]=0;
	up(i,0,n) f[0][n-i+n][i==0]=h[i];
	int mul=1;
	up(i,1,n) {
		int now=i&1, pre=now^1;
		up(j,-n,n) f[now][j+n][0]=f[now][j+n][1]=0;
		up(j,-n,n) {
			if(j<+n) {
				add(f[now][j+1+n][0],f[pre][j+n][0]*p[i]%P);
				add(f[now][j+1+n][1],f[pre][j+n][1]*p[i]%P);
			}
			if(j>-n) {
				add(f[now][j-1+n][0],f[pre][j+n][0]*q[i]%P);
				add(f[now][j-1+n][1],f[pre][j+n][1]*q[i]%P);
			}
		}
		add(f[now][n+n][1],f[now][n+n][0]), f[now][n+n][0]=0;
		int Ans=0;
		up(j,-n,n) add(Ans,f[now][j+n][1]);
		(mul*=ksm(p[i]+q[i]))%=P; 
		cout << (Ans%P+P)%P*mul%P << ' ';
	}
	cout << '\n';
}

signed main() {
//	freopen("1.txt","r",stdin);
	freopen("ziliang.in","r",stdin);
	freopen("ziliang.out","w",stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> T;
	while(T--) mian();
	return 0;
}