AT_apc001_f

首先考慮轉(zhuǎn)換邊權為點權，考慮令點權為連接的邊權異或和，這樣路徑異或變成了雙點修改，問清零的最小次數(shù)。

首先對于邊權和一樣的匹配不劣，問題是現(xiàn)在剩下一些孤單的旅人怎么匹配了，狀態(tài) dp 求出即可，注意只有 xor 和為 0
的狀態(tài)才存在（

---

AT_code_festival_2017_qualb_f

幽默，我為什么開這種題目。

首先不難發(fā)現(xiàn)，我們要構(gòu)造最小表示最大，我們求這個最小表示最大（

考慮三個字符串 \(s_1\leq s_2\leq s_3\)，那么肯定要放成 \(s_1s_3s_2\)（逃。

然后如果有一個 \(s_3\leq s_4\)，\(s_4\) 直接接在 \(s_1\) 后面即可，然后可以歸納 qwq

開一個 multiset，考慮每次取出最小最大的進行合并，最后即為答案。

---

AT_dwango2016qual_e

lsy 怎么做 lsy 題 /shui

Slope Trick ......？

首先題目不難轉(zhuǎn)化為給定一個序列 \(A\)（其實就是原題目中的 \(p\)，注意 \(t\) 不降），要構(gòu)造一個單調(diào)不降的序列 \(B\)，最小化 \(\sum |A_i-B_i|\)，特別的，要強制 \(t_i\) 一樣的 \(B_i\) 相等。

如果沒有最后那個強制其實就是 CF713C 了，我們描述一下這個 b 東西的做法，先考慮樸素的 dp，不妨設填完前 \(i\) 個 \(B\) 且 \(B_i=j\) 的最優(yōu)答案為 \(f[i][j]\)，那么轉(zhuǎn)移很顯然是 \(f[i][j]=\min_{k\leq j}\{f[i-1][k]\}+|a_i-j|\)，加上一個優(yōu)化，就有 \(f[i][j]=g[i-1][j]+|a_i-j|\) 了嘛，其中 \(g\) 是 \(f\) 的前綴 \(\min\)（

絕對值函數(shù)其實斜率單調(diào)遞減的說（對手指.png），那么其實不難發(fā)現(xiàn)，\(g\) 是一個下凸殼子，然后 \(f\) 也是一個下凸殼子，這里提前說明一下，對于這個題目加進去的是一個下凸函數(shù)，所以加進去其實也是一個下凸殼子捏，具體而言，斜率全都是單調(diào)遞增的，或者簡單一點的理解，前綴 \(\min\) 不影響凸性，然后每次斜率的變化都是 \(0~x-1\) 獲得 \(-1\)，\(x+1~inf\) 獲得 \(+1\)，這樣左邊永遠不會比右邊大 qwq

對于這個殼子，我們可以只維護拐點，拐點除斜率的變化量，和斜率為 \(0\) 的位置高度，如 image 所示的藍點為維護點，斜率變化幾就在堆里面放幾次，現(xiàn)在我們擁有了一個 priority 塞滿了藍點和一個 \(Ans\) 為斜率為 \(0\) 的位置的答案，q.top() 為斜率為 \(0\) 位置的起點。

然后怎么考慮呢，首先考慮 \(a_i\geq top\)，這種情況在 \(a_i\) 取最優(yōu)秀，最優(yōu)答案不變，直接在堆里面加入 \(a_i\) 即可。答案對了凸包其實還沒維護好，再 pop 掉平的點就行了。

然后考慮 \(a_i>top\)，這個時候其實還是 \(top\) 這個地方最優(yōu)秀，因為考慮 \(top\) 之前的斜率都是負的，加上這一個，最多變成平的，那么考慮 \(a_i\) 對 \(top\) 的貢獻，顯然是 \(top-a_i\)，加到 \(Ans\) 里面即可。

然后回到這個 lsy 題，我們需要同時加入 \(t_i\) 相等的再取前綴 \(\min\)，我們可以先維護頂點的斜率為 \(k\)，答案高度暫時為 \(Ans\)，如果 \(k>0\)，我們考慮退掉 \(top\)，考慮去掉 \(top\) 的貢獻，減掉 \(top\) 即可。換句話說，一個 \(a_i\) 對 \(Ans\) 的影響其實是斜率加 \(1\) 截距 \(-a_i\)，考慮到答案 \(k=0\) 前面的斜率影響就可以不管不顧了。

---

P10383

我們考慮在模意義下求解，然后還原分數(shù)，所以我們?nèi)∫粋€超大質(zhì)數(shù) \(9000000000000000041\)，然后就做完了。

首先對于模大質(zhì)數(shù)可以還原出合法解，就是要說明對于 \(0\leq p,q\leq V,M>V^2\)，對于任意的 \(mul\gets \frac{p}{q}\mod M\) 都可以還原出唯一的對應的 \(\frac{p}{q}\)。

那么考慮一組 \(\frac{p}{q}\equiv \frac{p_2}{q_2}\pmod M\)，有 \(M|pq_2-q_p2\)，考慮到 \(0\leq p,q,p_2,q_2\leq A\)，那么只能 \(\frac{p}{q}=\frac{p_2}{q_2}\) 了。

還原是考慮一組 \(\frac{a}{x}\equiv\frac{b}{y}\equiv \frac{y\mod x}{b-a\lfloor\frac{y}{x}\rfloor}\pmod M\)，前面兩個是定的給的且等于 \(mul\)，第三個是新的構(gòu)造，每一輪重新取后面兩個，正確性大概是這樣（

把 \(mul\) 換成 \(\frac{x}{a},\frac{y}{b}\) 之后正確性顯然。

但是不能通過 sub4 的兩個點，考慮強制 \(a\) 也有約束，但是還有一個點會整活出 \(y=0\) 這種東西。大概是輾轉(zhuǎn)相除不夠充分遍歷導致的，我也不會啊，求教。

其實正確的合并是使用 bgst，但是不知道這個 exgcd 東西有沒有前途，反正感覺簡潔就記了 /xia

遞歸出 \(y=0\) 的 hack 是 2841300223 2499598500。

upt on 2024.9.29 錯誤是沒有 int128 導致的。

---

P5513

不難發(fā)現(xiàn)按照完全二叉樹那種編號方式（先層再列順次標號）之后，操作分別對應 \(\times 2,\times 2+1,\lfloor\frac{ }{2}\rfloor,-1,+1\)，不妨維護其二進制數(shù)，分別對應 \(后面放一個 0/1,去掉一位,平凡的二進制數(shù) +1/-1\)。

這個 \(+1/-1\) 可能會導致進位退位，不能直接做完，那我們考慮直接加在位上面，最后再一起進位。

但這樣子是不對的，如果不及時進位可能會導致本位多舍去一些數(shù)，那么我們只需要在每次做右移操作前進一位就行了，復雜度沒問題，正確性有了。

答案怎么求，首先無腦的，二進制位長的那個無腦往上條調(diào)到同一深度，然后考慮同時跳，調(diào)到一層考慮差的絕對值，枚舉層數(shù)對貢獻取 \(\min\) 就行了，注意層數(shù)從小到大枚舉，二進制差太大了就直接不繼續(xù)做了。

---

P3642

首先有一個樸素的方程，設 \(f_u(x)\) 表示在子樹 \(u\) 用 \(x\) 秒燃爆的最小代價，那么顯然有轉(zhuǎn)移 \(f_u=\sum_{v 是 u 的兒子}\{f_v(y)+|x-w-y|\}\)，首先 \(f_u\) 是一個凸包。

我們枚舉考慮合并 \(u,v\)，那我們不妨考慮 \(v\) 帶給 \(f_u\) 的增量函數(shù) \(F_{v\to u}\)，我們考慮一個位置 \(x\) 在函數(shù) \(g(y)=f_v(y)+|x-w-y|\) 上面的最小值，這個最小值就是 \(F_{v\to u}\) 在 \(x\) 上面的縱坐標，我們畫出 \(f_v\) 和 \(|(x-w)-y|\) 進行分類討論，首先凸包相加還是凸包，然后斜率為 \(0\) 的位置一定最優(yōu)，然后設 \(f_v\) 斜率等于 \(0\) 的是 \([L,R]\) 這一段，設 \(Jury=\min\{f_v(i)\}\)。

• 對于 \(x-w<L\) 即 \(x<L+w\)，抬平之后 \(L\) 以及左邊一段斜率為 \(0\)，如果 \(x\geq L\) 可以取到 \(L\)，最優(yōu)值為 \(Jury+(L+w)-x\)，不然 \(x<L\)，取 \(x\) 最優(yōu)，答案是 \(f_v(x)+|x-w-x|\) 也就是 \(f_v(x)+w\)。

• 對于 \(L\leq x-w\leq R\)，取 \(x-w\) 最優(yōu)，答案為 \(Jury\)（

• 對于 \(R<x-w\)，取 \(R\) 最優(yōu)，最優(yōu)答案是 \(Jury+x-(w+R)\)。

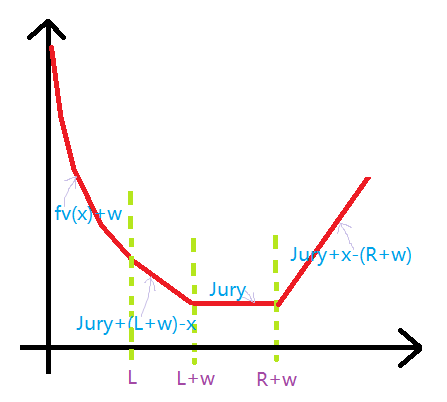
我們考慮畫出圖來，先向上平移，然后發(fā)現(xiàn)將 \(f_v\) 變成 \(F_{v\to u}\) 只需要先退出 \(>L\) 的后面的節(jié)點，然后再強制加入后面三條線段即可，于是考慮對 \(f_v\) 做點手腳然后跟 \(f_u\) 合并起來，合并可以使用可并堆或者啟發(fā)式合并。

這樣其實已經(jīng)做完了，但是方便實現(xiàn)還有一些小東西補充，首先對于最后的堆，我們知道截距為 \(\sum_{i=2}^N w_i\)，知道所有點的斜率單調(diào)遞增且最后一位是 \(0\)（至少我們可以選擇性的做成這樣，然后我們可以考慮直接還原出斜率為 \(0\) 的地方的答案了，換句話說，我們只維護拐點已經(jīng)可以解除答案了，就不需要再維護一些亂七八遭的東西，設堆從大到小的橫坐標是 \(a_1,...,a_k\)，答案是 \(Ans=\sum w_i+\sum_{i=1}^k (w_k-w_{k+1})\times k)=\sum w_i-\sum a_i\)。

然后我們考慮 \(f_u\) 直接加入了 \(cnt\) 個兒子，此時立起來的斜率就是 \(cnt\)，我們要的圖像斜率最后為 \(1\)，所以 pop 掉 \(cnt-1\) 個就行了，特別的，\(f_1\) 要多 pop 掉一個。

---

ABC217H

攻擊是往里面塞一次函數(shù)，是凸的，直接在堆里面維護就好了，然后考慮這個走來走去，不妨設距離上一次攻擊的時間間隔為 \(d\)，上一個包斜率為 \(0\) 的部分是 \([L,R]\)，那么就是 \(L\) 左邊的向左平移 \(d\)，\(R\) 右邊的向右平移 \(d\)，不妨開大根/小根堆維護斜率 \(<0\)/\(\geq 0\) 的拐點，平移操作直接打 tag，每次加入射線分討貢獻即可。

---

CF436E

比較顯然且錯誤的做法是一顆一顆拿，每次考慮拿最小的，拿了 \(a_i\) 之后把 \(b_i-a_i\) 當成一棵新的星星考慮，但這顯然是錯誤的。但是我們延續(xù)拿了 \(a_i\) 之后放入 \(b_i-a_i\) 作為一棵新星星的做法。

上述錯誤啟示我們必須把 \(a,b\) 一起考慮，那我們考慮兩個兩個拿，不妨設最小和次小的一棵星星為 \(a_i,a_j\)，最小的一組星星為 \(b_i\)，哪個更優(yōu)我們拿哪個，拿完之后更新 \(a,b\) 的集合，實現(xiàn)可以用 multiset。

這樣我們做完了 \(2|w\) 的情況，那么對于這個剩余的 \(w\)，我們考慮幾種情況，「將拿了零個的升級為 1 個」，「將一個拿了一個的升級為 2 個」，「將拿了兩個的降級為 1 個 & 將拿了零個的升級為 2 個」 以及 「將拿了一個的降級為 0 個 & 將拿了零個的升級為 2 個」，這幾種取最優(yōu)就是答案了。

事實上后面那一部分是 \(w\gets w+1\) 的做法，可以用這個做整個題目，那樣的話要開好多好多堆。

---

P4574/P1633

考慮 dp，不妨設 \(f[d][i][j][k]\) 表示 \(0,\dots,i\) 位用了 \(a/b/c\) 中的 \(i/j/k\) 個 \(1\) 時的最小 \(c\)，轉(zhuǎn)移很簡單，但是有點小長就不贅述了，注意判斷算出來 \(f\) 超過指定位數(shù)的情況無解。

---

CF633F

樹形 dp，感覺做麻煩了，不妨設 \(f[i][0/1/2][0/1]\) 表示子樹 \(i\) 中開了 \(j\) 條鏈最后一條直徑有沒有端點在跟 的最大點權和，轉(zhuǎn)移很暴力，分類討論就好了，不難但有點小長，這里不再贅述。

---

AGC013D

首先考慮操作，「黑球變黑球：黑白」，「白球變白球：白黑」，「黑球變白球：黑黑」和「白球變黑球：白白」。

考慮一個操作序列的合法性，大概是一個增量極差不超過 \(n\)，不妨放在坐標系上面考慮，點 \((x,y)\) 表示第 \(x\) 次操作有 \(y\) 個白球，操作序列在坐標系上面連成一條折線，只要不越界就合法，走勢分別為 \((x,y)\to (x+1,y+1)/(x,y)\to (x+1,y)/(x,y)\to (x+1,y+1)/(x,y)\to (x+1,y)\)，能使用一個走勢要求至少有一個其對應的球，在這題就是有 \(y=0\) 和 \(y=n\) 的系數(shù)特殊性。

我們考慮 dp 折線數(shù)，設 \(f[i][j]\) 表示 \((i,j)\) 位結(jié)尾的答案，然后發(fā)現(xiàn)這樣子會算重，我們考慮去重。

先思考怎么樣子的折線是重復的，對于極差 \(d=n\) 的一定不會算重，所以考慮 \(d<n\) 的。首先形狀相同，可以通過上下平移獲得，那我們比較想考慮碰到 \(y=0\) 的折線，但是這樣有一個問題是系數(shù)變的不統(tǒng)一了，指對于 \(d=n\) 的在最底下需要 \(\times 1\)，而 \(d<n\) 的需要 \(\times 2\)，我們不妨考慮在 \(y=1\) 這個地方也計算一次貢獻，這樣子就正確了。

---

P3266

寫完就有一種被騙了的感覺，解數(shù)，結(jié)束，感覺有點小陰間，也可能單純我太菜 /kk

首先每一行單調(diào)遞增，值域 \([0,m]\) 填進 \(m\) 個里面，那么不妨設 \(f[i][j]\) 表示做到第 \(i\) 行，空出了 \(j\) 的解數(shù)，轉(zhuǎn)移顯然有 \(f[i][j]=\sum_{k=0}^{j+1}f[i-1][k]\)，其實也就是 \(f[i][0]=f[i-1][0]+f[i-1][1],f[i][j(>0)]=f[i][j-1]+f[i-1][j+1]\)，我們把這個放在坐標系上面，考慮組合意義，就是走完的方案數(shù)。

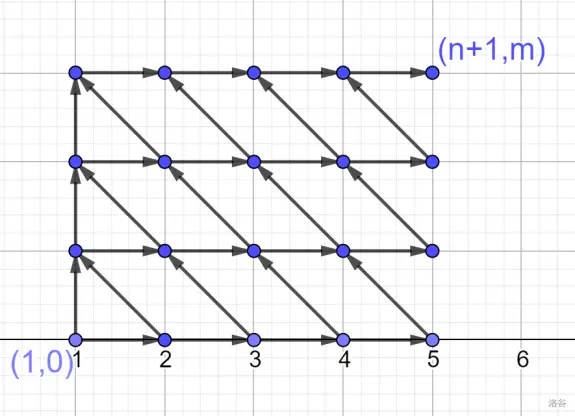
這是題解的圖，媽耶整個題解區(qū)都是這種說不上詭不詭異的坐標方式，但是考慮到我在 AGC013D 也是這么標的那么還是看的挺順眼的。然后其實好像這個題這么畫確實最好看（

這個圖太丑了，不妨考慮平移，得到下圖，這個等價。

考慮終點 \((s,t)\) 關于 \(A\) 的對稱點 \((s',t')\)，不難發(fā)現(xiàn)碰到過 \(A\) 的折線跟 \((0,0)\) 到 \((s',t')\) 的路徑形成雙射，于是可以計數(shù)了。

然后我們考慮先到達 \(A\) 的解，不難發(fā)現(xiàn)其實就是上述轉(zhuǎn)換后「總解數(shù)」-「先到達 \(B\) 的解」。

我們要考慮不碰到兩條綠色線的方案數(shù)，容斥，答案是「總解數(shù) \(\binom{2n+m+1}{n}\)」-「先碰到 \(A\) 的方案數(shù)」-「先碰到 \(B\) 的方案數(shù)」，先碰到 \(A\) 的方案數(shù)為 「走到 \((s',t')\) 的方案數(shù)」-「走到 \((s',t')\) 且碰到過 \(B\) 的方案數(shù)」，跟原本的題目本質(zhì)相同，可以遞歸計算。

---

CF1870E

不妨設 \(f[i][j]\) 表示前 \(i\) 個數(shù)能否做出 \(j\)，樸素轉(zhuǎn)移要 \(O(n^3)\)，無法通過此題，狀態(tài)難以縮小，考慮優(yōu)化轉(zhuǎn)移。

對于 \(\text{mex}(l,r)=\text{mex}(l-1,r)\) 或者 \(\text{mex}(l,r)=\text{mex}(l,r-1)\) 的區(qū)間顯然沒什么考慮的必要，那我們只考慮 \(\text{mex}(l,r)\neq \text{mex}(l+1,r)\) 且 \(\text{mex}(l,r)\neq \text{mex}(l,r-1)\) 的區(qū)間 \((l,r)\)，事實上，這種區(qū)間個數(shù)上界只有 \(2n\)。

對于一個左端點 \(l\)，我們考慮其合法右端點 \(r\)，首先不會有 \(a_l=a_r\)，否則一定不滿足條件，不妨設 \(a_l>a_r\)，那么 \(a_l<a_r\) 同理，那么分析性質(zhì)：因為 \(\text{mex}(l,r)\neq \text{mex}(l+1,r)\)，所以 \(\text{mex}(l+1,r)=a_l\)，差不多的，也有 \(\text{mex}(l+1,r-1)=a_r\)，我們考慮 \((l,l+1/l+2/l+\dots)\) 的區(qū)間 \(\text{mex}\)，這顯然是單調(diào)不降的，然后合法的 \(r\) 的 \(\text{mex}\) 其實就是區(qū)間 \(\text{mex}\) 從 \(a_r\) 變成 \(a_l\) 的那個點，這種顯然最多只有一個，于是總的也不是很多了嘛（

---

P4542

答案肯定可以拆成不超過 \(k\) 條鏈，這些鏈是覆蓋所有點且每條鏈單調(diào)。我們考慮對一個拆分怎么計算答案，我們維護 \(d_i\) 表示走到 \(i\) 的最小答案，\(Ans\) 表示目前總的最小時間，我們按照排列順序 \(0,\dots,n\) 更新答案，當前編號是 \(x\)，那么 \(d_x=d_{x 的父親}+x 跟父親不經(jīng)過 >x 的點的最短路\)，個數(shù)從上面繼承。

然后不難了，考慮用網(wǎng)絡流解決，一個流對應一條鏈，首先 繼承&必須走 不妨拆出雙點，不妨按照下述方式建圖：\(S\to L_0:k/0,L_i\to R_i:1/-\infty,L_i\to R_i:\infty/0,R_i\to T:\infty/0,R_i\to L_j:\infty,len_{i,j}\)，最后一個顯然要求 \(i<j\)，于是做完了......？

---

P8860

首先對于一條邊刪除多次的顯然只有第一次有效，我們把刪除時間放在邊上作為權，沒有被刪除的不妨隨便欽定刪除時間為 \(q+1,q+2,\dots\)，這個其實是為了沒有權值重復的好考慮一點。

直接做太困難了，倒流時間好像也做不了，但是確實可以離線，于是顯然要求出最后保留的一條 \(1\to n\) 的路徑，如果有多條，隨便保留一條就可以了。

我們思考什么樣的路徑更優(yōu)，最小值最大的最優(yōu)，如果最小值一樣，那就次小值最大的最優(yōu)，這個顯然可以最短路套主席樹維護，主席樹上面要維護一個二進制哈希，然后就做完了。

但是這個主席樹重載太他媽傻逼了，比想象中難調(diào)些。其實也有簡單做法，按照最終答案從小到大考慮，每次更新最小的那個，不難證明這是對的。

---

AGC006F

考慮將黑點 \((x,y)\) 看成邊 \(x\to y\)，加邊相當于 \(x\to y\to z\) 貢獻一個 \(z\to x\)。

不妨先考慮鏈怎么做，\(x\to y\to z\) 兩兩貢獻一個，\(x\to y\to z\to k\) 這個 \(k\) 能跟 \(y,z\) 貢獻，多玩一點不難發(fā)現(xiàn)，對于位置編號在模 \(3\) 意義下不同的兩個點有貢獻，不妨設模 \(3\) 為 \(0/1/2\) 的個數(shù)分別為 \(A/B/C\)，貢獻就是 \(AB+AC+BC\)，這個結(jié)論可以推廣到樹上，只不過變成了相鄰點給相鄰權，進一步的，可以推廣到帶環(huán)的圖上，要求是環(huán)長是 \(3\) 的倍數(shù)，特別的，如果剩余系里面少了某種點貢獻是原本邊數(shù)。

然后考慮環(huán)長不是 \(3\) 的倍數(shù)的環(huán)，比如 \(x\to y\to z\to k\to x\)，手玩發(fā)現(xiàn)是全聯(lián)通的，再考慮加入新的邊，發(fā)現(xiàn)可以繼續(xù)全聯(lián)通，是一個 \(點數(shù)^2\) 的貢獻。

所以染色然后計算貢獻即可，注意算的時候需要及時處理反邊。

---

CF1140F

不妨考慮建立二分圖，一個聯(lián)通塊 \(l\) 個行 \(r\) 個列答案就是 \(\sum l\times r\)，線段樹分治即可。

---

CF277D

每次都被簡單 01 背包弄急眼是為什么 /fad

首先 bf 是人生的真理，不難發(fā)現(xiàn)肯定先打完暴力再去打困難部分。因為先打困難部分再去打別的簡單題罰時肯定會吃到，后打不一定會吃到。

然后考慮 dp，設 \(f[i][j]/g[i][j]\) 表示前 \(i\) 題用了 \(j\) 分鐘的最大期望 / 最小罰時，不難寫出轉(zhuǎn)移 \(f[i][j]=\max\{f[i-1][j],f[i-1][j-s]+a,f[i-1][j-s-t]+a+(1-p)b\}\)，\(g\) 分別是 \(g[i-1][j],g[i-1][j-s]+s,(g[i-1][j-s-t]+s)p+(1-p)j\)。

然后發(fā)現(xiàn) \(g\) 的答案跟背包順序相關，套路的寫個價格比較的貪心就行了，轉(zhuǎn)移可以寫個結(jié)構(gòu)體封裝一下之類的。

---

AT_dp_v/CF543D

首先考慮計算 \(Ans_1\)，是一個簡單 dp，\(f[i]=\prod_{j 是 i 的兒子}(f[j]+1)\)，然后考慮換根，顯然 \(Ans[i]=\frac{Ans[fa]}{f[u]+1}f[u]\)，但是這個 \(f[u]+1\) 可能沒有逆元。

那么不妨考慮在每一位考慮一個 \(f+1\) 的前后綴積，每次再傳入一個扣掉子樹的答案作為參數(shù)，于是就做完了。

---

P7730

首先考慮差分，變成單點的操作，然后差分數(shù)組的正負放到二分圖上面，然后操作表示流動即可。

---

P7863

這個飛行次數(shù)需要獨立出來，我們不妨考慮拆鏈，我們考慮一個總的路線 \(S\to R_0\to L_1\to R_1\to \dots\to L_{m-1}\to R_{m-1}\to L_m\to S\)，其中 \(S\to R_0,L_m\to s,L_i\to R_i\) 是跳躍，否則是飛行。

不難發(fā)現(xiàn)這個起點是用來搞笑的，我們直接把 \(L_m,R_0\) 分進一組，換句話說，使 \(R_m\gets R_0\)。然后在上面畫上貢獻，有 \(Ans=\sum_{i=1}^m h[L_i]-h[R_i]\)，換句話說，其實就是鏈長之和（

這樣怎么費用流其實都是好約束的，我們直接一點的考慮這個飛行次數(shù)最少，其實接兩條鏈就少一次費用，于是考慮建出二分圖做最大匹配，剩下都是簡單東西（雖然好像上面也都是簡單東西？）。

---

loj 535 花火

先求出逆序?qū)Γ紤]最優(yōu)的交換貢獻，先翻轉(zhuǎn)序列，把 \((x,a_x)\) 放在坐標軸上，不難發(fā)現(xiàn)要求的是以 \((i,a_i),(j,a_j)(i<j)\) 為左下/右上角的矩形中的點數(shù)的最大值，然后考慮亂搞，不難想到只有左下方?jīng)]有點的點能作為左下角，右上方?jīng)]有點的的點能作為右上角，考慮能作為左下角/右上角的點集為 \(L,R\)，發(fā)現(xiàn)按照橫坐標排序之后縱坐標單調(diào)，畫一下發(fā)現(xiàn)交叉小于包含，具有決策單調(diào)性，于是可以做了。

---

P7599

先處理出 st 表，左邊右邊的到達點 \(lt_i,rt_i\)。

首先考慮單點 \(l\to r\)，必要條件是 \(\max_{i=l}^{r-1} \{a_i\}<a_r\)，手玩貪心不難發(fā)現(xiàn)盡量走大的，但是不能走超過 \(a_r\) 的。

拓展到序列，起點終點其實是不定的，不妨令 \(Y\gets \max_{i=c}^d\{a_i\}\)，考慮把 \([a,b]\) 更新為其有解的區(qū)間 \([a',b]\)，起點就是里面的 rmq。

注意到難以直接欽定終點，不妨令 \(Y\gets \max_{i=st}^{c-1}\{a_i\}\)，我們先強制欽定 \(<Y\) 的隨便跳，我們對結(jié)果分類討論：如果 \(lt[x]\) 是不可愉悅的鴻溝，不斷往右跳直到 \(>C\) 即可，否則下一位能跳到的較大值也得 \(\leq Y\)，因為 \(>Y\) 的一定只能在左邊，然后這種不超過兩步就能跳到，做進去就行了，大段跳使用倍增實現(xiàn)，復雜度查詢一個 \(\log\)。

---

AT_agc028_c

在機房還沒想出來，去小賣部買了點抹茶面包就會做了（

首先這個邊權和答案都取 \(\min\)，所以邊權的 \(\min\) 可以拆開不要，次數(shù)正確最小化答案就行了。

有貢獻的點一定是 \(n\) 個，我們考慮原題目的其中 \(n\) 個點怎樣才算合法。不妨令取的位為 \(1\) 否則為 \(0\)，四種方案分別為 11/00/01/10，不難發(fā)現(xiàn) 第一種&第二種個數(shù)相同，合法條件就是可以拼成環(huán)并且相鄰位不能都為 \(1\)。

再來個小分討：如果沒有第一第二種，第三/第四種只能有一種，就是 \(\sum_{i=1}^{n}a_i,\sum_{i=1}^{n}b_i\) 是可以的，然后有第一第二種的話任意情況合法，可以考慮一下構(gòu)造，拿出一個 11，然后 10/01 直接接在 左/右，如果還有別的 11/00，配對塞入即可，這些操作后得到的還是那個兩邊都是 \(1\) 的大串，最后再用初始的 11 所匹配的 00 接上環(huán)即可。

于是可以枚舉一位強制選 11，剩下的取前 \(n-2\) 大即可，維護可以寫一個對頂堆狀物的兩個 multiset。

---

AT_agc043_d

首先考慮 A,B,C 這樣順次是一段的，如果有前一個比后一個大，那么拿完前面之后會立即拿后面的那個，考慮最終序列，是由若干個長度為 \(1/2/3\) 的段組成的，段內(nèi)單調(diào)下降，端頭單調(diào)上升。

但是這個條件比較的不充分，比如說全都是 \(2\) 的其實不合法，首先 \(3\) 的個數(shù)與原題目一致其實無所謂的，那么就需要 \(1\) 的段數(shù) \(>\) \(2\) 的段數(shù)，不妨用 \(f[i][j]\) 表示前 \(i\) 個數(shù)分成 \(\lceil 1 的段數(shù)\rfloor -\lceil 2 的段數(shù)\rfloor\) 為 \(j\) 的方案數(shù)，直接轉(zhuǎn)移即可。

---

P5395

這個 \(\frac{1}{m!}\) 的盒子相同的貢獻我們最后再乘進去。

題目求的答案就是恰好 \(0\) 個位置為空的方案數(shù)，不好直接求，考慮容斥，不妨令 \(f(k)/g(k)\) 為 恰好/欽定 \(k\) 個位置為 \(0\) 的方案數(shù)，那么顯然有 \(g=(m-k)^n\binom{n}{k}\)。

其實顯然還有 \(g(k)=\sum_{i=k}^{n}f(k)\binom{i}{k}\)，反演可得 \(f(k)=\sum_{i=k}^{n}g(k)\binom{i}{k}(-1)^{i-k}\)。

然后帶入 \(g\) 得到 \(Ans(m)=f(0)=\frac{1}{m!}\sum_{i=0}^{n}(-1)^i\binom{m}{i}(m-i)^n=\sum_{i=0}^{n}\frac{(-1)^i}{i!}\times \frac{(m-i)^n}{(m-i)!}\)，卷積，使用 NTT 即可（

---

P4859

首先轉(zhuǎn)化為恰好 \(k\gets \frac{n+k}{2}\) 組 \(a_i>b_i\)，然后考慮欽定的貢獻怎么求，之后二項式反演帶進去就行了。

欽定 \(k\) 組的方案數(shù)考慮 dp，因為有偏序關系不妨使得 \(a\uparrow,b\uparrow\)，令 \(L_i\) 表示比 \(a_i\) 小的 \(b_j\) 的個數(shù)，設 \(dp[i][j]\) 表示前 \(i\) 個欽定 \(j\) 組的方案數(shù)，不難得到 \(f[i][j]=f[i-1][j]+f[i-1][j-1]\times (L_i-j+1)\)，然后就做完了。

---

P6478

套路的進行二項式反演，然后變成了求欽定 \(k\) 輪非平局的方案數(shù)，這個直接樹形 dp 就行了，轉(zhuǎn)移跟 P4859 差不多，只不過是要先拼一個背包再考慮貢獻。

---

P4320

直接廣義圓方樹就行了。

---

CF1355F

就，晚上睡覺的時候突然會做了......？

因數(shù)個數(shù) \(Ans=\prod_{x_i 為質(zhì)數(shù) p_i 的指數(shù)} (x_i+1)\)，首先 \(>\sqrt {10^8}\) 質(zhì)數(shù)只有 \(\times 1/\times 2\) 的貢獻，題目限制那么寬松不妨先不考慮，我們篩出范圍里面的質(zhì)數(shù)來考慮。

往 \(p\in[\sqrt{\sqrt{n}},\sqrt{n}]\) 的 \(p\) 的數(shù)量去討論的，這個次數(shù)其實也不是很多，并且跟更大的也有約束，然后發(fā)現(xiàn)其實只篩到 \(\sqrt{\sqrt{n}}\) 然后篩滿的話，\(4Ans\) 這種東西就挺好的，但是還是不夠，在一個分討下面不行。

那個教主做法感覺比較不好寫對，感覺這個 \(\gcd\) 的詢問其實能得到的東西無法拓展，就是好像不太能直接得到什么很厲害的東西（

但是其實也不難改，隨便篩一點 \(>\sqrt{\sqrt n}\) 的質(zhì)數(shù)的話就對了吧，反正到了兩次根號（\(純素數(shù)積 + x 的不超過一次\)）之后還有剩下來的次數(shù)剛剛好夠（

我們考慮從小到大的素數(shù)，如果存在這個素數(shù)就考慮升次之后還有沒有，不斷這樣考慮，每次盡量多詢問，最后輸出 \(2\times Ans\) 就可以通過了。

---

AGC006D

向無聊世界宣戰(zhàn)！（

首先考慮二分，把 \(a\) 攤成 01 序列 \(b\)，現(xiàn)在考慮頭頂是不是 \(\geq mid\)。

自己打個標，發(fā)現(xiàn)一段的 010101 有一個金字塔的貢獻且邊緣顏色等于旁邊顏色，于是我們考慮連續(xù)的 0/1 的位置貢獻的最好值，注意特判掉一直 01 循環(huán)的情況。

---

CF354C

經(jīng)典套路，跟 ARC068E 差不多，按照線段長度排序雙指針即可。

但是這個題目不能數(shù)論分塊，可以弄一點 \(n\log n\) 的枚舉加一個小小的樹狀數(shù)組（