知識性總結(jié)

• 群論。群論主要講的就是 Burnside 引理和 Polya 定理，都是計數(shù)技巧。主要解決一類本質(zhì)不同問題，核心思想是找到題目中的置換群，對于每種置換統(tǒng)計不動點(diǎn)數(shù)量。在統(tǒng)計不動點(diǎn)數(shù)量時常常會與各種組合計數(shù)技巧搭配。

• 字符串。這學(xué)期主要講了后綴數(shù)組、自動機(jī)和回文自動機(jī)。回文自動機(jī)主要處理和回文相關(guān)問題，也有些題目在回文樹上進(jìn)行 dp。后綴數(shù)組相較于后綴自動機(jī)而言就是在處理后綴排序上比較簡便。

  后綴自動機(jī)作用確實挺大，用極少的狀態(tài)卻儲存了整個字符串的信息。通過反串建后綴自動機(jī)可以建出后綴樹，很多題目都需要在后綴樹上求答案，用其兩個后綴的 lcp 即為其 lca 的 len 的性質(zhì)。所以經(jīng)常結(jié)合一些數(shù)據(jù)結(jié)構(gòu)如 lct 等樹上常見問題。

• 線性代數(shù)。線性代數(shù)部分主要講的線性基與矩陣樹。線性基主要處理集合異或相關(guān)問題，并且可以延伸到樹上。因其 \(O(\log^2 n)\) 合并常常結(jié)合 st 表處理一些區(qū)間問題。

  矩陣樹主要考察圖論建模，當(dāng)然也能進(jìn)行很多擴(kuò)展操作。本質(zhì)是求所有生成樹邊權(quán)乘積的和，當(dāng)然也可以拓展為許多重定義生成樹權(quán)值的問題，主要是靠重定義乘法。

• 多項式。首先是拉格朗日插值。拉格朗日插值核心思想是 crt，通常在題目中作為輔助出現(xiàn)。如果通過打表或者其它方式發(fā)現(xiàn)題目的答案是一個多項式，則可以先求出小規(guī)模的答案再拉插出需要的值。

  多項式部分就是 fft、ntt 和 fwt。一般是優(yōu)化一些計數(shù)，當(dāng)然也需要推式子和組合計數(shù)的能力，特別是一些需要容斥的題目。本質(zhì)上是找到一種線性變換。

• 數(shù)據(jù)結(jié)構(gòu)。數(shù)據(jù)結(jié)構(gòu)部分講了點(diǎn)分治、splay、虛樹和 lct。點(diǎn)分治主要解決關(guān)于樹上路徑相關(guān)問題，核心思想就是找重心為分治重心，統(tǒng)計經(jīng)過該點(diǎn)路徑的答案，然后再再對子樹分治處理；如果是動態(tài)的，一般要考慮建出點(diǎn)分樹，再用數(shù)據(jù)結(jié)構(gòu)進(jìn)行維護(hù)。

  splay 基本上能維護(hù)線段樹的常見信息，主要是通過 splay 操作維持樹的平衡，而 splay 又包含左旋和右旋操作，通過這些操作將樹的高度變低，以支持查詢；lct 則是類似樹鏈剖分，通過實邊和虛邊將多棵 splay 連接在一起，以維護(hù)動態(tài)圖。核心是 access 操作，將該點(diǎn)到根的上面掛的 splay 合并到一起，從而支持刪加邊操作。要特別注意區(qū)分原樹和輔助樹（splay）。

  

  

  虛樹的話，就是只提取出樹中的關(guān)鍵點(diǎn)以達(dá)到減少規(guī)模的效果，常見于多組詢問給出關(guān)鍵點(diǎn)或樹的規(guī)模很大但關(guān)鍵點(diǎn)少的題目中。多組詢問直接建樹即可；關(guān)鍵點(diǎn)少一般樹會有特殊形態(tài)，利用其性質(zhì)建樹。

  • 建樹。本質(zhì)上是用單調(diào)棧維護(hù)一條右鏈。首先按 dfn 進(jìn)行排序，并將 \(1\) 號點(diǎn)入棧。然后對于點(diǎn) \(a_i\)，先求出它與棧頂 \(s\) 的 lca \(l\)，如果 \(l\) 等于 \(s\)，則直接入棧就行了（說明 \(a_i\) 與 \(s\) 在一條鏈中）；否則則彈到第一個 dfn 大于 \(l\) 的元素 \(t\) 和下一個元素 \(p\)，如果 \(p\ne l\)，那么 \(l\) 應(yīng)該代替 \(p\) 的位置。然后將 \(a_i\) 替代 \(t\) 成為新的右鏈。彈棧則表示已經(jīng)確定，所以直接連邊即可。
    

• 雜項。包括 wqs 二分、SW 和最小斯坦納樹。wqs 二分主要解決限制個數(shù)且代價函數(shù)具有凸性的題目，通過減去二分的額外代價轉(zhuǎn)換成簡單的無個數(shù)限制的問題，根據(jù)切點(diǎn)與題目限制作比較進(jìn)行求解。一般是打表驗證，可以考慮從四邊形不等式模型或費(fèi)用流模型等方向證明。

  

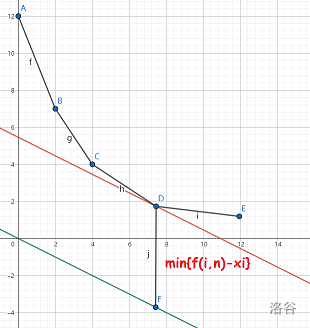
  SW 和最小斯坦納樹考察較少，SW 思想是遞歸，另一個是狀壓。

考試總結(jié)

總述

T1 花了大概 \(40\) 分鐘，主要是在數(shù)列長度上卡了一會兒。然后在 T2 上花了很多時間，主要是思路想偏了。T3 雖然記憶中做過，但是沒有去細(xì)想，打了 T3 和 T4 的暴力后又回去看 T2 了。

優(yōu)點(diǎn)的話就是暴力分都打了。

問題及解決方案

• T2 思路想偏并耗時過久。當(dāng)時覺得 \(u\) 只可能是某個階乘，就考慮怎么枚舉過后快速求。并且在求兩個階乘間的距離時沒有仔細(xì)思考導(dǎo)致浪費(fèi)了許多時間。當(dāng)時想過直接建虛樹，但是沒有往這個方向深入思考。

  • 首先在得出一個結(jié)論后不要立馬去實現(xiàn)，先考慮到底正不正確，是否存在反例，并且要思考存不存在更簡便的寫法，避免浪費(fèi)時間。
  • 其次在寫代碼前要先將細(xì)節(jié)思考全面后再按框架寫，不要來回調(diào)補(bǔ)，效率低下。
  • 最后不要在一個題上面浪費(fèi)大量時間，一定要先看看后面的題是否有更容易想的。并且心態(tài)很重要，在決定跳題時就不要被前面的題所影響，否則到頭來什么都做不好。

• T3 思考不周。即使 T3 不是原題也應(yīng)該很快得出結(jié)論，更何況是原題應(yīng)該有一點(diǎn)模糊的想法，當(dāng)時可能心思主要還是放在 T2 上導(dǎo)致沒有仔細(xì)思考。在開題的時候也應(yīng)該先想一會別急著寫。

  開題的時候一定要先通讀完并有一定的思考后才開始做題，不然容易因突發(fā)狀況導(dǎo)致后面的題缺失足夠的思考。

總結(jié)及展望

總結(jié)

通過又是半學(xué)期的學(xué)習(xí)，套路也是不斷地在積累。平時時不時地一定要去復(fù)盤總結(jié)，不然是很容易遺忘的。

平時學(xué)的知識基本上都認(rèn)真去進(jìn)行消化了，但是有些沒有復(fù)習(xí)還是有些遺忘。除了作業(yè)表的題外，也可以找一點(diǎn)其他題做，熟悉一下算法思想和相關(guān)技巧。

在編寫代碼的時候一定要好好想清想透再寫，一定要梳理好框架，已經(jīng)有幾次吃了這種虧了。

賽后的題一定要及時補(bǔ)，將題目的營養(yǎng)汲取干凈。

CF 還是太忙了沒打幾場，雖然上了點(diǎn)分但還是沒有達(dá)到預(yù)期。其實即使沒有打也可以下來后看一看想一想，主要去提升一下思維和積累一些技巧，提升還是很大的。

在平時的練習(xí)中，能明顯感覺得到之前一些薄弱的環(huán)節(jié)在逐步提高，但是還是要不斷練習(xí)、積累技巧（計數(shù)、數(shù)據(jù)結(jié)構(gòu)）。

展望

馬上又是中考，下次回機(jī)房又要等到下次了。所以還是對未來做點(diǎn)展望。

• 在下一個周期中，CSP-S \(360+\)，NOIP \(320+\)。
• CF \(2200+\)。