深度學習基礎課：卷積層的后向傳播推導

大家好~本課程為“深度學習基礎班”的線上課程，帶領同學從0開始學習全連接和卷積神經網絡，進行數學推導，并且實現可以運行的Demo程序

線上課程資料：

本節課錄像回放1

本節課錄像回放2

本節課錄像回放3

加QQ群，獲得ppt等資料，與群主交流討論：106047770

本系列文章為線上課程的復盤，每上完一節課就會同步發布對應的文章

本課程系列文章可進入索引查看：

深度學習基礎課系列文章索引

回顧相關課程內容
為什么要學習本課
主問題：如何推導卷積層的后向傳播？
主問題：如何反向計算誤差項？
- 結學
任務：實現反向計算誤差項
主問題：如何計算Filter每個權重值的梯度？
- 結學
任務：實現計算Filter每個權重值的梯度
總結
參考資料
擴展閱讀

回顧相關課程內容

卷積神經網絡的局部連接和權重共享是指什么？
卷積層的前向傳播是如何計算的？
全連接層的后向傳播算法是什么？
答：先計算輸出層的誤差項，然后反向依次計算每層的誤差項直到與輸入層相連的層，最后根據每層的誤差項和輸入得到每層的梯度
誤差項的計算公式是什么？
答：\(\delta_k=\frac{dE}{dnet_k}\)
全連接層的后向傳播是如何推導？

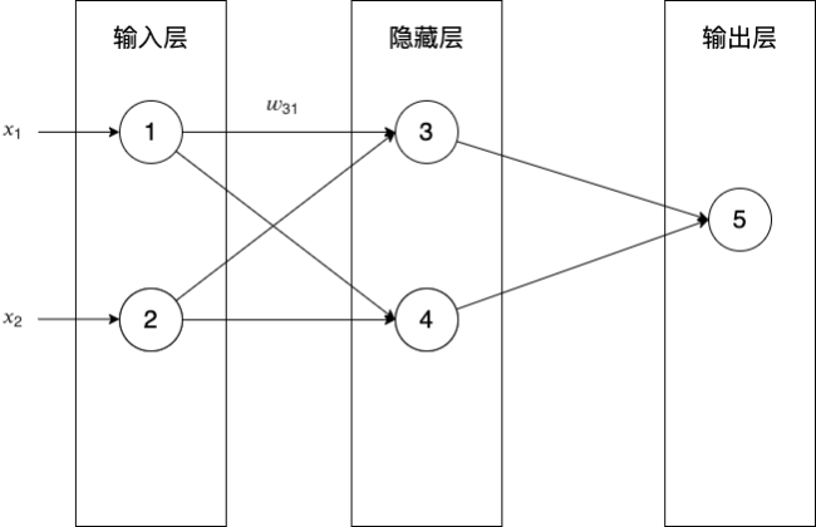
為什么要學習本課

如何推導卷積層的后向傳播？

主問題：如何推導卷積層的后向傳播？

卷積層的后向傳播算法有哪些步驟？
答：
1.已知下一層計算的誤差項，反向依次計算這一層的誤差項
2.計算這一層中每個權重值的梯度
與全連接層中隱藏層的后向傳播算法的步驟一樣嗎？有什么區別？
答：步驟跟隱藏層是一樣的，但是每個步驟的計算方法都不一樣，這是因為：
“局部連接”使得第一步誤差項的計算方法不一樣；
“權值共享”則使得第二步變為計算Filter中的每個權重值的梯度；
下面分別討論這兩個步驟的實現

主問題：如何反向計算誤差項？

我們先來考慮步長為1、輸入的深度為1、filter個數為1的最簡單的情況。
假設輸入的大小為33，filter大小為22，按步長為1卷積，我們將得到2*2的feature map。如下圖所示：
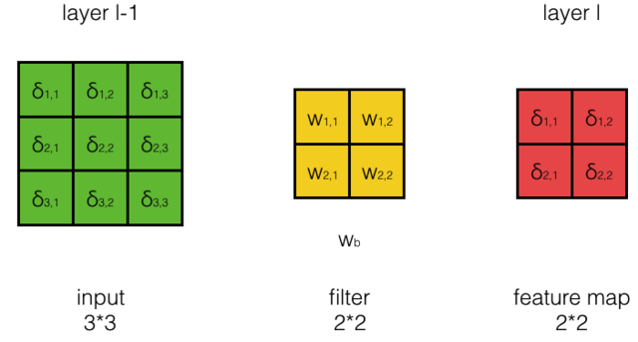
其中layer l-1為當前層（卷積層），layer l為下一層
在這里，我們假設第l層中的每個誤差項都已經算好，我們要做的是計算第l-1層每個神經元的誤差項
它的計算公式是什么：

\[\delta_{i,j}^{l-1}=? \\ \delta_{i,j}^{l-1}表示第l-1層第i行第j列的誤差項 \]

答：

\[\begin{aligned} \delta_{i,j}^{l-1} &= \frac{dE}{dnet_{i,j}^{l-1}} \\ &= \frac{dE}{da_{i,j}^{l-1}}\frac{da_{i,j}^{l-1}}{dnet_{i,j}^{l-1}}\\ \end{aligned} \]

\[a_{i,j}^{l-1}表示第l-1層第i行第j列神經元的輸出 \\ net_{i,j}^{l-1}表示第l-1層第i行第j列神經元的加權輸入 \\ \]

如何求\(\frac{dE}{da_{i,j}^{l-1}}\)？
- 我們先來看幾個特例，然后從中總結出一般性的規律：
  - 計算\(\frac{dE}{da_{1,1}^{l-1}}\)？
    答：
    \( 因為a_{1,1}^{l-1}只與net_{1,1}^l有關，且net_{1,1}^l = w_{1,1}a_{1,1}^{l-1} + w_{1,2}a_{1,2}^{l-1} + w_{2,1}a_{2,1}^{l-1} + w_{2,2}a_{2,2}^{l-1} + w_b \\ 所以\frac{dE}{da_{1,1}^{l-1}}=\frac{dE}{dnet_{1,1}^{l}}\frac{dnet_{1,1}^l}{da_{1,1}^{l-1}} = \delta_{1,1}^l w_{1,1} \)
  - 計算\(\frac{dE}{da_{1,2}^{l-1}}\)？
    答：\( 因為a_{1,2}^{l-1}與net_{1,1}^l, net_{1,2}^l有關，且\\ net_{1,1}^l = w_{1,1}a_{1,1}^{l-1} + w_{1,2}a_{1,2}^{l-1} + w_{2,1}a_{2,1}^{l-1} + w_{2,2}a_{2,2}^{l-1} + w_b \\ net_{1,2}^l = w_{1,1}a_{1,2}^{l-1} + w_{1,2}a_{1,3}^{l-1} + w_{2,1}a_{2,2}^{l-1} + w_{2,2}a_{2,3}^{l-1} + w_b \\ 所以\frac{dE}{da_{1,2}^{l-1}}=\frac{dE}{dnet_{1,1}^{l}}\frac{dnet_{1,1}^l}{da_{1,2}^{l-1}} + \frac{dE}{dnet_{1,2}^{l}}\frac{dnet_{1,2}^l}{da_{1,2}^{l-1}} \\ = \delta_{1,1}^l w_{1,2} + \delta_{1,2}^l w_{1,1} \)
  - 請總結出規律？
    答：\( 不難發現，計算\frac{dE}{da_{i,j}^{l-1}}，相當于把第l層誤差項的周圍補一圈0，再與180度翻轉后的filter進行互相關操作，就能得到想要結果，如下圖所示： \)
    
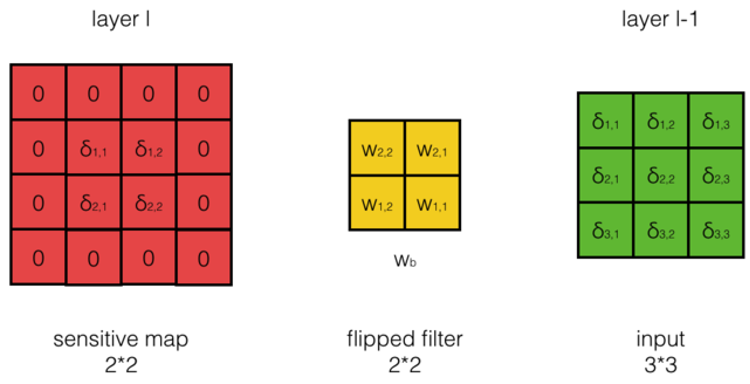
    計算公式是什么？
    答：
    \( \frac{dE}{da^{l-1}} = cross(padding(\delta^l), rotate180(W)) \\ \)
如何求\(\frac{da_{i,j}^{l-1}}{dnet_{i,j}^{l-1}}=?\)

答：

\[\because a_{i,j}^{l-1} = f(net_{i,j}^{l-1}) \\ \therefore\frac{da_{i,j}^{l-1}}{dnet_{i,j}^{l-1}}= f'(net_{i,j}^{l-1}) \]

因此，我們得到了最終的公式：

\[\begin{aligned} \delta^{l-1} &= \frac{dE}{dnet^{l-1}} \\ &= \frac{dE}{da^{l-1}}\frac{da^{l-1}}{dnet^{l-1}} \\ &= cross(padding(\delta^l), rotate180(W)) \circ f'(net^{l-1}) \\ \end{aligned} \]

\[其中：\\ \delta^{l-1}, \delta^l, W, net^{l-1}都是矩陣\\ 符號\circ為element \, wise \, product，即將矩陣中每個對應元素相乘 \]

下面我們來推導步長為S的情況
我們來看看步長為2與步長為1的差別：
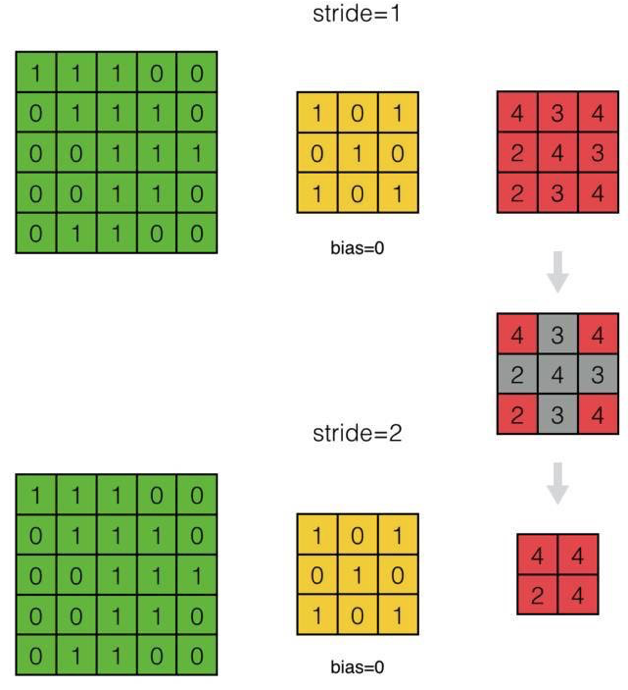
如何處理步長為2的情況？
- 如何將其統一為步長為1的情況？
  答：我們可以看出，因為步長為2，得到的feature map跳過了步長為1時相應的部分。因此，當我們反向計算誤差項時，我們可以對步長為S的\(\delta^l\)相應的位置進行補0，將其『還原』成步長為1時的\(\delta^l\)
下面我們來推導深度為D和Filter個數為N的情況
如果把每個深度看成一個結點，把互相關操作變成乘上權重，則深度為3、Filter個數為2的情況如下圖所示：
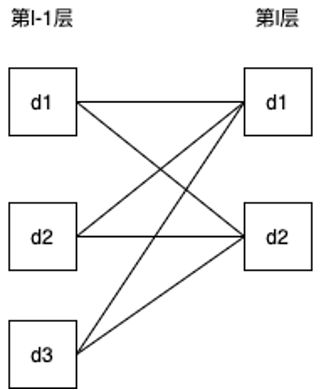
第l-1層的d1影響了第l層的哪幾個結點？
答：影響了第l層的所有結點，包括第l層的d1,d2
所以第l-1層的d1的誤差項應該等于什么？
答：\(= 第l層的d1的誤差項與第一個Filter反向計算出的第l-1層的誤差項 + 第l層的d2的誤差項與第二個Filter反向計算出的第l-1層的誤差項\)
因此，可以將誤差項計算公式改為什么？
答：

\[\begin{aligned} \delta_d^{l-1} &= \sum_{n=0}^{N-1} cross(padding(\delta_n^l), rotate180(W_{d, n})) \circ f'(net^{l-1}) \\ \end{aligned} \]

\[其中：\\ d為深度序號，即第d層\\ n為Filter的序號，即第n個Filter\\ \]

結學

如何反向計算誤差項？

任務：實現反向計算誤差項

請實現反向計算誤差項？
答：待實現的函數為ConvLayer->bpDeltaMap函數，實現后的函數為：ConvLayer->bpDeltaMap函數

主問題：如何計算Filter每個權重值的梯度？

我們要在得到本層的誤差項的情況下，計算本層的Filter的權重的梯度

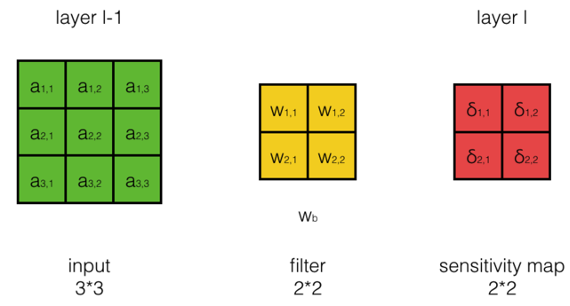
\[如上圖所示，a_{i,j}^{l-1} 是第l-1層的輸出，W_{i,j}是第l層filter的權重，\delta_{i,j}^{l} 是第l層的誤差項。我們的任務是計算W_{i,j}的梯度，即\frac{dE}{dw_{i,j}}\\ 為了計算偏導數，我們需要考察權重W_{i,j}對E的影響：\\ 權重項W_{i,j}通過影響net_{i,j}^l的值，進而影響E \\ 我們仍然通過幾個具體的例子來看權重項W_{i,j}對net_{i,j}^l的影響，然后再從中總結出規律。 \]

計算\(\frac{dE}{dw_{1,1}}\)？
- \(w_{1,1}對哪幾個net_{i,j}^l有影響？\)

答：

\[net_{1,1}^l = w_{1,1}a_{1,1}^{l-1} + w_{1,2}a_{1,2}^{l-1} + w_{2,1}a_{2,1}^{l-1} + w_{2,2}a_{2,2}^{l-1} + w_b \\ net_{1,2}^l = w_{1,1}a_{1,2}^{l-1} + w_{1,2}a_{1,3}^{l-1} + w_{2,1}a_{2,2}^{l-1} + w_{2,2}a_{2,3}^{l-1} + w_b \\ net_{2,1}^l = w_{1,1}a_{2,1}^{l-1} + w_{1,2}a_{2,2}^{l-1} + w_{2,1}a_{3,1}^{l-1} + w_{2,2}a_{3,2}^{l-1} + w_b \\ net_{2,2}^l = w_{1,1}a_{2,2}^{l-1} + w_{1,2}a_{2,3}^{l-1} + w_{2,1}a_{3,2}^{l-1} + w_{2,2}a_{3,3}^{l-1} + w_b \\ \]

\[從上面的公式看出，由于權值共享，權值W1,1對所有的net_{i,j}^l有影響\\ 因為E是所有所有的net_{i,j}^l的函數，而所有的net_{i,j}^l又都是w_{1,1}的函數\\ 所以根據全導數公式，計算\frac{dE}{dw_{1,1}}是要把每個偏導數都加起來：\\ \]

\[\begin{aligned} \frac{dE}{dw_{1,1}} &= \frac{dE}{dnet_{1,1}^l}\frac{{dnet_{1,1}^l}}{dw_{1,1}} + \frac{dE}{dnet_{1,2}^l}\frac{{dnet_{1,2}^l}}{dw_{1,1}} + \frac{dE}{dnet_{2,1}^l}\frac{{dnet_{2,1}^l}}{dw_{1,1}} + \frac{dE}{dnet_{2,2}^l}\frac{{dnet_{2,2}^l}}{dw_{1,1}} \\ &= \delta_{1,1}^l a_{1,1}^{l-1} + \delta_{1,2}^l a_{1,2}^{l-1} + \delta_{2,1}^l a_{2,1}^{l-1} + \delta_{2,2}^l a_{2,2}^{l-1} \end{aligned} \]

計算\(\frac{dE}{dw_{1,2}}\)

答：

\[\begin{aligned} \frac{dE}{dw_{1,2}} &= \delta_{1,1}^l a_{1,2}^{l-1} + \delta_{1,2}^l a_{1,3}^{l-1} + \delta_{2,1}^l a_{2,3}^{l-1} + \delta_{2,2}^l a_{2,3}^{l-1} \end{aligned} \]

實際上，每個權重項導數的計算都是類似的，我們不一一舉例了
現在，是我們再次發揮想象力的時候，我們發現計算\(\frac{dE}{dw_{i,j}}\)的規律是什么？

答：

\[\frac{dE}{dw_{i,j}} = \sum_m \sum_n \delta_{m,n}^l a_{i+m, j+n}^{l-1} \]

也就是用誤差項作為卷積核，在input上進行互相關操作，如下圖所示：

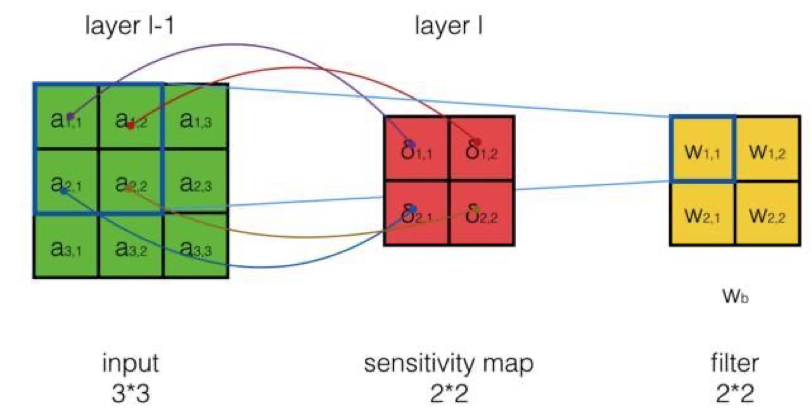
如何求偏置項的梯度\(\frac{dE}{dw_b}\)？

答：

\[\begin{aligned} \frac{dE}{dw_b} &= \frac{dE}{dnet_{1,1}^l}\frac{dnet_{1,1}^l}{w_b} + \frac{dE}{dnet_{1,2}^l}\frac{dnet_{1,2}^l}{w_b} + \frac{dE}{dnet_{2,1}^l}\frac{dnet_{2,1}^l}{w_b} + \frac{dE}{dnet_{2,2}^l}\frac{dnet_{2,2}^l}{w_b} \\ &= \delta_{1,1}^l + \delta_{1,2}^l + \delta_{2,1}^l + \delta_{2,2}^l \\ &= \sum_i \sum_j \delta_{i,j}^l \end{aligned} \]

\[ 也就是偏置項的梯度就是所有誤差項之和 \]

如何處理步長為2的情況？

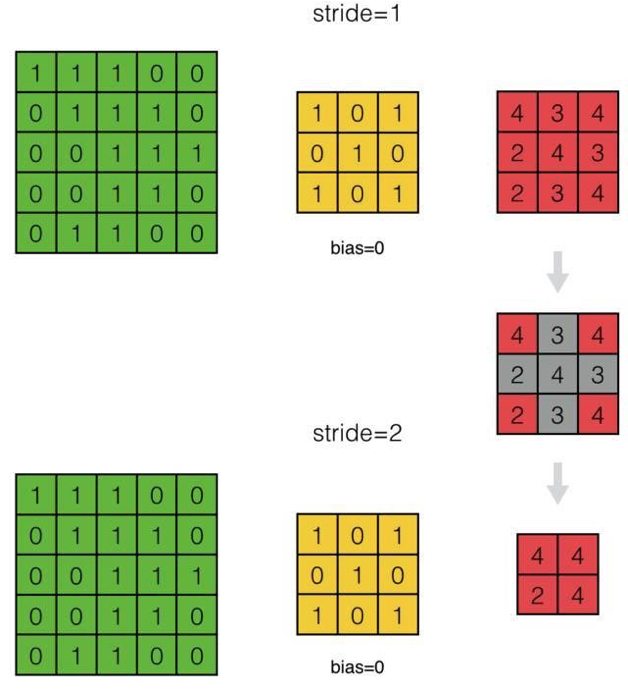
答：對于步長為S的卷積層，處理方法與傳遞誤差項時一樣：通過對\(\delta^l\)補0，將其『還原』成步長為1的情況

對于Filter個數為N和每個Filter的深度為D的情況，因為每個都對應輸出圖像的對應深度的Feature map和輸入圖像的對應深度的Feature map，每一個二維Filter只涉及到一次二維卷積運算
所以只需分別計算N×D次每個二維Filter的導數，再將其組合成4維張量，即可求得整個Filter的導數

結學

如何計算Filter每個權重值的梯度？

任務：實現計算Filter每個權重值的梯度

請實現計算Filter每個權重值的梯度？
答：待實現的代碼為：ConvLayer_compute_gradient，實現后的代碼為：ConvLayer_compute_gradient_answer, Filter_answer

總結

請總結本節課的內容？
請回答開始的問題？

參考資料

零基礎入門深度學習 | 第四章：卷積神經網絡
卷積神經網絡(CNN)反向傳播算法推導

擴展閱讀

卷積神經網絡(CNN)反向傳播算法推導
有詳細的數學推導(比如本課程中通過找規律得到的公式，在該文中有數學推導)

posted @ 2022-12-26 08:13 楊元超閱讀(120) 評論(0) 收藏舉報

刷新頁面返回頂部