深度學習基礎課：最大池化層的前向傳播推導

大家好~本課程為“深度學習基礎班”的線上課程，帶領同學從0開始學習全連接和卷積神經網絡，進行數學推導，并且實現可以運行的Demo程序

線上課程資料：

本節課錄像回放

加QQ群，獲得ppt等資料，與群主交流討論：106047770

本系列文章為線上課程的復盤，每上完一節課就會同步發布對應的文章

本課程系列文章可進入索引查看：
深度學習基礎課系列文章索引

回顧相關課程內容

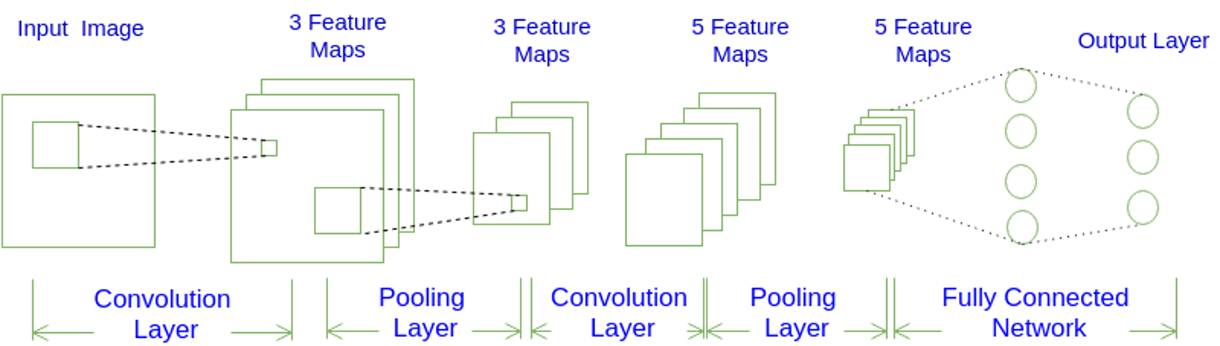
• 卷積神經網絡的常用架構模式是是什么？
• 最大池化層在卷積神經網絡中的作用是什么？

為什么要學習本課

• 如何推導最大池化層的前向傳播？

主問題：如何推導最大池化層的前向傳播？

• 最大池化層的輸入和輸出是什么？
  
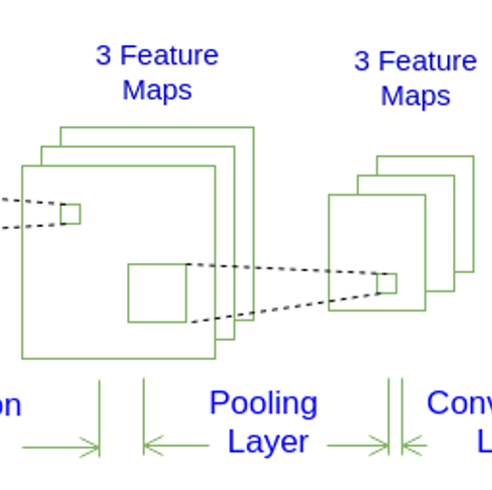
  答：輸入是上一層（卷積層）輸出的多個Feature Map，輸出是對每個Feature Map進行了下采樣后的多個Feature Map，其中輸出的Feature Map的個數與輸入的個數相同

• 最大池化層是否包含Filter？
  答：是

• Filter的作用是什么？
  答：Filter屬于抽象的概念，并沒有實際的值。它的作用是取對應區域的最大值

• 有幾個Filter？
  答：1個

• 假設有一個\(4*4\)的Feature Map，使用一個\(2*2\)的filter和步幅為2的最大池化層，得到一個\(2*2\)的Feature Map，如下圖所示：
  

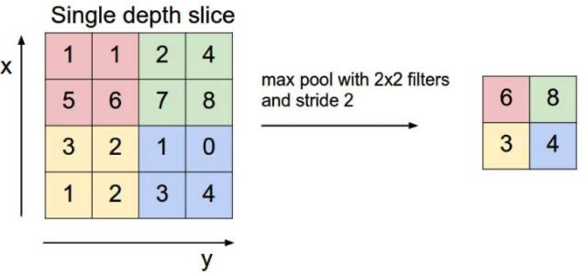
• 計算的公式是什么？
  答：

• 如果輸入Feature Map的深度大于1，計算的公式是什么？
  答：

• 如何計算輸出Feature Map大小？

答：

任務：實現最大池化層的前向傳播

• 請實現最大池化層的前向傳播？
  答：待實現的代碼為：MaxPoolingLayer，實現后的代碼為：MaxPoolingLayer_answer
• 請運行最大池化層的代碼，檢查前向傳播的輸出是否正確？
  答：在Test.init函數中，構造了輸入數據和MaxPooling Layer；
  在Test.test函數中，進行了前向傳播并打印了結果。
  結果為兩個Feature Map，它的數據如下所示：

["f:",[
    [2,2,[3,2,1,2]],
    [2,2,[5,2,2,2]]
    ]]

我們可以手動計算下\(a_{0,0,0}\)，結果等于3，與輸出的結果相同，證明forward的實現是正確的