大家好~本課程為“深度學習基礎班”的線上課程，帶領同學從0開始學習全連接和卷積神經網絡，進行數學推導，并且實現可以運行的Demo程序

線上課程資料：

本節課錄像回放1

本節課錄像回放2

加QQ群，獲得ppt等資料，與群主交流討論：106047770

本系列文章為線上課程的復盤，每上完一節課就會同步發布對應的文章

本課程系列文章可進入索引查看：
深度學習基礎課系列文章索引

回顧相關課程內容

• 如何使用全連接神經網絡識別手寫數字？
  

  • 網絡結構是什么？

為什么要學習本課

• 全連接神經網絡用于圖像識別任務有什么問題？
  

• 卷積神經網絡是怎樣解決這些問題的？

• Relu激活函數是什么？

• 如何推導卷積層的前向傳播？

主問題：卷積神經網絡是什么？

為什么引入卷積神經網絡？

• 全連接神經網絡用于圖像識別任務有什么問題？

答：

1、參數數量太多

考慮一個輸入1000*1000像素的圖片，輸入層有1000*1000=100萬節點。假設第一個隱藏層有100個節點，那么僅這一層就有(1000*1000+1)*100=1億參數！
而且圖像只擴大一點，參數數量就會多很多，因此它的擴展性很差。

2、沒有利用像素之間的位置信息

對于圖像識別任務來說，每個像素和其周圍像素的聯系是比較緊密的，和離得很遠的像素的聯系可能就很小了。如果一個神經元和上一層所有神經元相連，那么就相當于對于一個像素來說，把圖像的所有像素都等同看待，這不符合前面的假設。當我們完成每個連接權重的學習之后，最終可能會發現，有大量的權重，它們的值都是很小的(也就是這些連接其實無關緊要)。努力學習大量并不重要的權重，這樣的學習必將是非常低效的。

3、網絡層數限制

我們知道網絡層數越多其表達能力越強，但是通過梯度下降方法訓練深度全連接神經網絡很困難，因為全連接神經網絡的梯度很難傳遞超過3層。因此，我們不可能得到一個很深的全連接神經網絡，也就限制了它的能力。

• 卷積神經網絡是怎樣解決這些問題的？

答：

1、局部連接

這個是最容易想到的，每個神經元不再和上一層的所有神經元相連，而只和一小部分神經元相連。這樣就減少了很多參數。

2、權值共享

一組連接可以共享同一個權重，而不是每個連接有一個不同的權重，這樣又減少了很多參數。

3、下采樣

可以使用池化（Pooling）來減少每層的樣本數，進一步減少參數數量，同時還可以提升模型的魯棒性。

主問題：卷積神經網絡是什么？

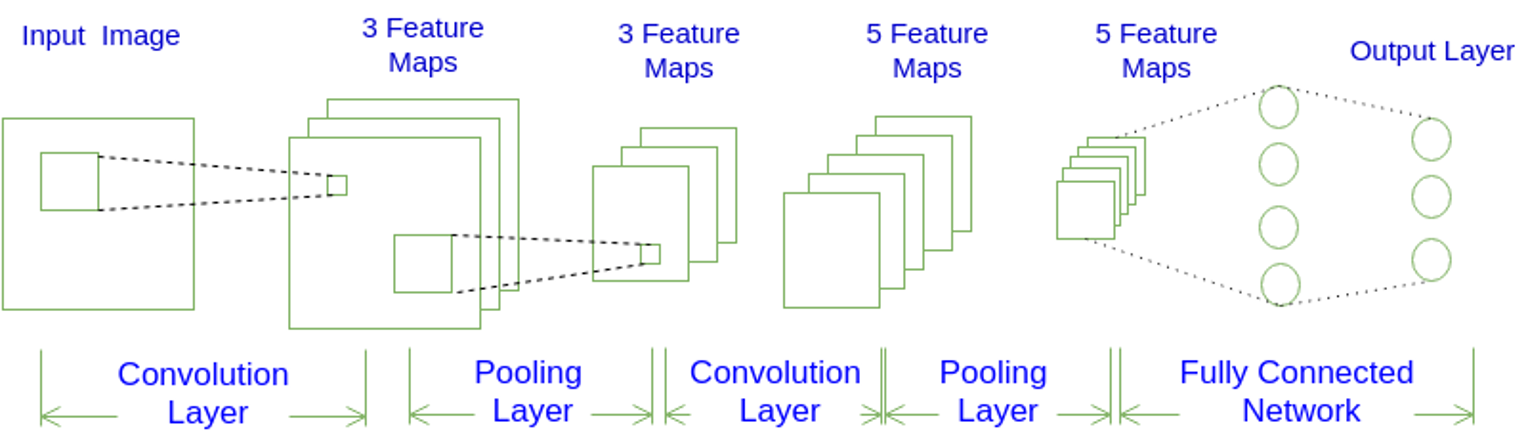
• 如圖1所示，一個卷積神經網絡由若干卷積層、池化層、全連接層組成

• 常用架構模式為：INPUT -> [[CONV]N -> POOL?]M -> [FC]*K

• 也就是N個卷積層疊加，然后(可選)疊加一個池化層，重復這個結構M次，最后疊加K個全連接層

• 圖1的N、M、K為多少？
  答：N=1, M=2, K=2

• 與全連接神經網絡相比，卷積神經網絡有什么不同？
  全連接神經網絡：
  

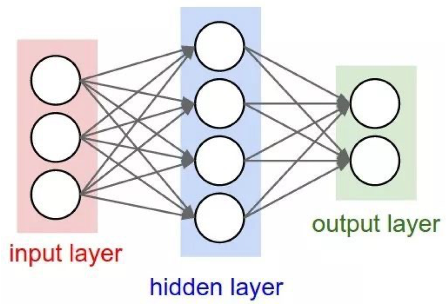
• 什么是Filter？Filter與卷積層是什么關系？
  答：Filter是卷積核，是一組參數，用來提取特征到Feature Map中。Filter的寬度和高度一般是相等的。
  卷積層包含多個Filter

• Filter的數量與Feature Map的數量有什么關系？
  答：卷積層包含的Filter的數量和卷積層輸出的Feature Map的數量是相等的，一一對應的

• 如何理解Feature Map？
  答：Feature Map保存了Filter提取的特征。如一個Filter為提取圖像邊緣的卷積核，那么對應的Feature Map就保存了圖像邊緣的特征

• 池化層在做什么？
  答：下采樣，即將Feature Map縮小

• 全連接層跟Feature Maps如何連接？
  答：全連接層的神經元跟所有的Feature Map的像素一一對應，如Feature Maps有5個，每個有30個像素數據，那么與其連接的全連接層就有150個神經元

• 請整體描述圖1卷積神經網絡的前向傳播過程？

主問題：Relu激活函數是什么？

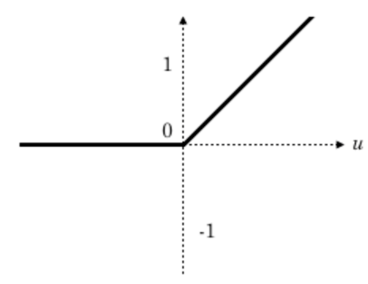
• Relu的定義是什么？
  答：\(f(x)=max(0,x)\)
  

• 與Sigmoid相比，Relu有什么優勢？
  答：

1、速度快

2、減輕梯度消失問題

全連接隱藏層的誤差項公式如下，它會乘以激活函數的導數：

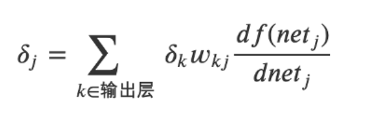
而Sigmoid激活函數的導數的圖形如下所示：

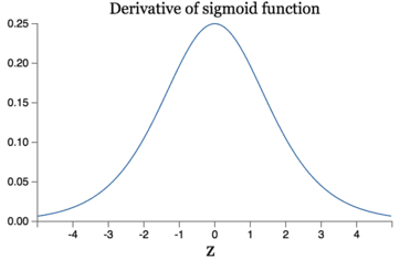
可知它的導數的最大值為\(\frac{1}{4}\)，所以第一個全連接隱藏層的誤差項會至少衰減為原來的\(\frac{1}{4}\)，上一個全連接隱藏層的誤差項則至少衰減為原來的\(\frac{1}{16}\)，以此類推，導致層數越多越容易出現梯度消失的問題

而Relu的導數為1，所以不會導致誤差項的衰減

3、稀疏性

通過對大腦的研究發現，大腦在工作的時候只有大約5%的神經元是激活的。有論文聲稱人工神經網絡在15%-30%的激活率時是比較理想的。因為relu函數在輸入小于0時是完全不激活的，因此可以獲得一個更低的激活率。

任務：實現Relu激活函數

• 請實現Relu激活函數
  答：待實現的代碼為：ReluActivator，實現后的代碼為：ReluActivator_answer

主問題：如何推導卷積層的前向傳播？

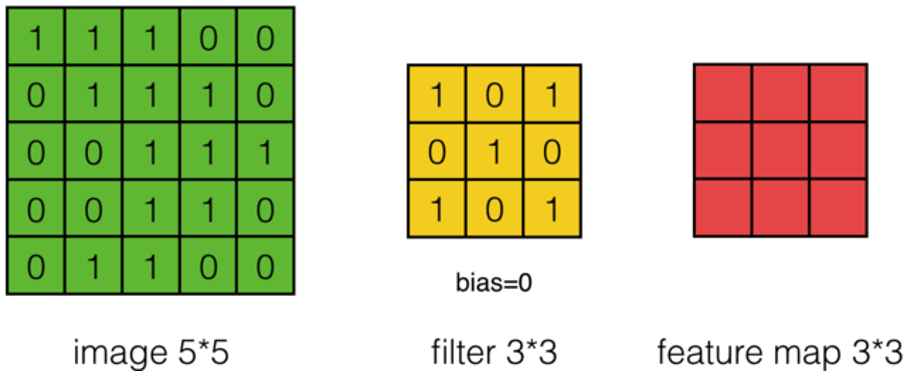
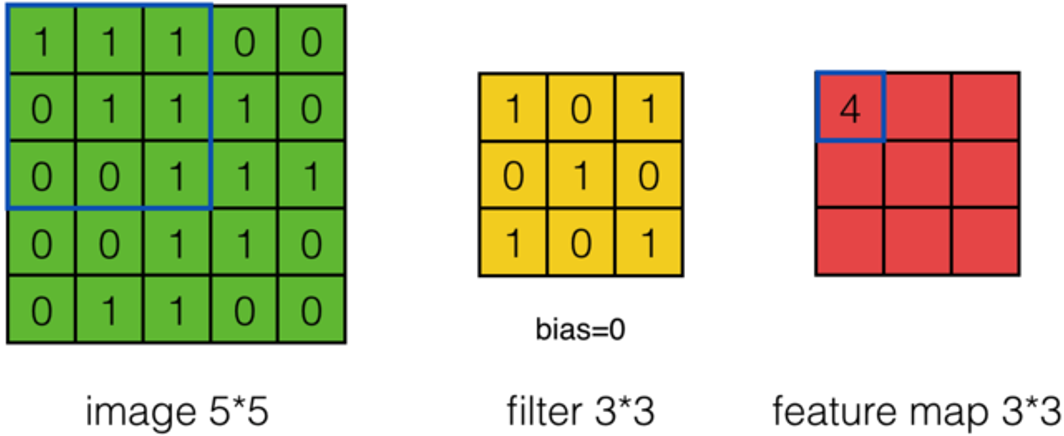
• 假設有一個55的圖像，使用一個33的filter進行卷積，想得到一個3*3的Feature Map，如下圖所示：
  

• 使用下列公式計算卷積：

• \(a_{0,0}=?\)
  答：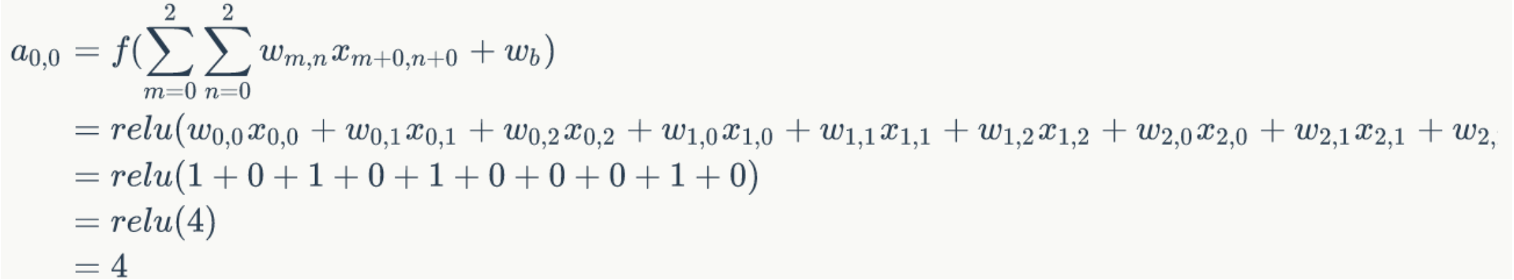
  

• \(a_{0,1}=?\)
  答：
  

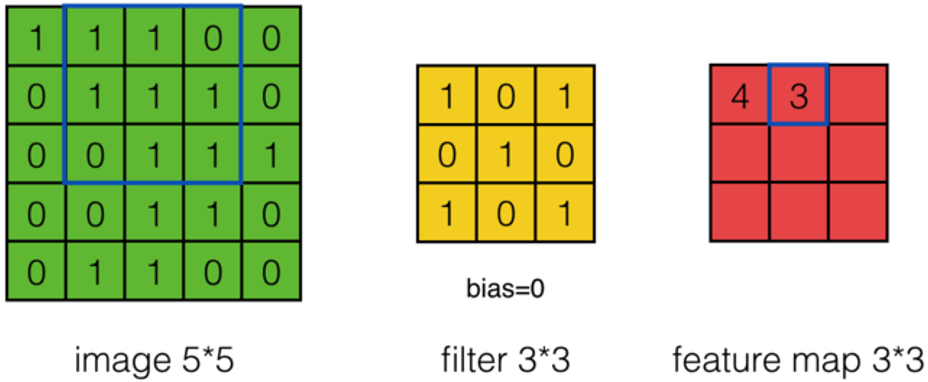
• 可以依次計算出Feature Map中所有元素的值。下面的動畫顯示了整個Feature Map的計算過程：
  

• 上面的計算過程中，步幅(stride)為1。步幅可以設為大于1的數。例如，當步幅為2時，Feature Map計算如下：
  
  
  
  

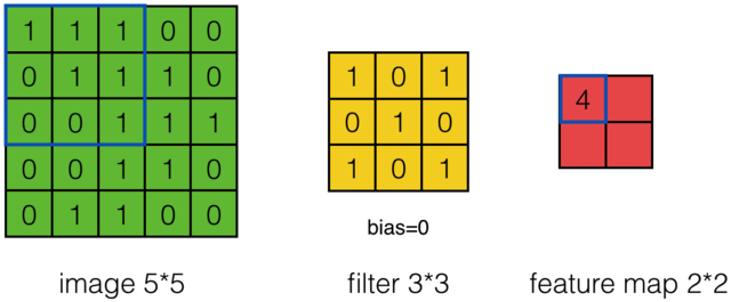
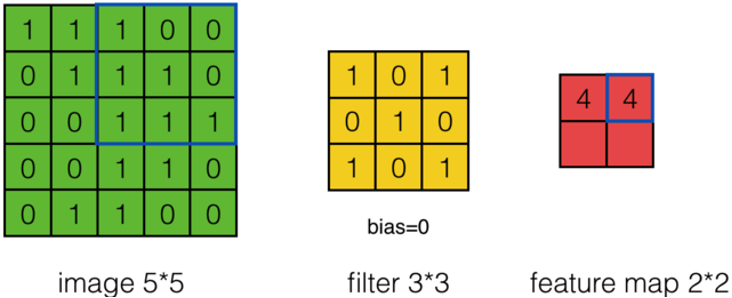
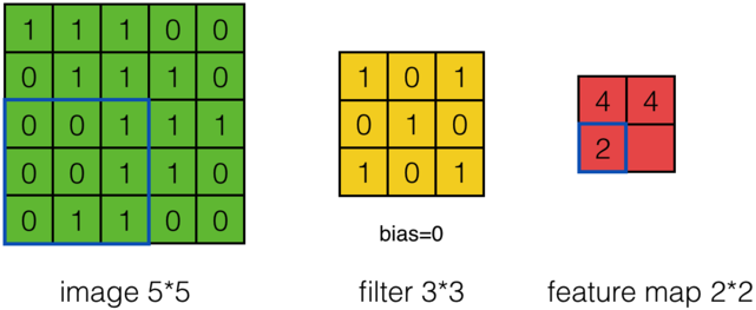
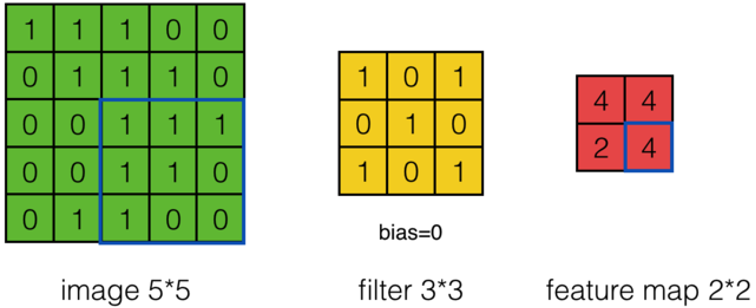
• 我們注意到，當步幅設置為2的時候，Feature Map就由\(3*3\)變成\(2*2\)了。這說明圖像大小、Filter的大小、步幅、卷積后的Feature Map大小是有關系的

• 它們滿足什么關系？

答：

• 什么是Zero Padding？
  答：Zero Padding是指在原始圖像周圍補幾圈0
• 為什么引入Zero Padding？
  答：Zero padding對于圖像邊緣部分的特征提取是很有幫助的
• 引入Zero Padding后，卷積后的Feature Map大小的公式應該修改為什么？
  答：

• 前面我們已經講了深度為1的卷積層的計算方法，如果深度大于1怎么計算呢（步幅為1）？
  答：

• 每個卷積層可以有多個filter。每個filter和原始圖像進行卷積后，都可以得到一個Feature Map。因此，卷積后Feature Map的深度(個數)和卷積層的filter個數是相同的
• 它的計算公式是什么（步幅為1）？
  答：

• 下面的動畫顯示了包含兩個filter的卷積層的計算
  \(7*7*3\)輸入->經過兩個\(3*3*3\)filter (步幅為2)->得到了\(3*3*2\)的輸出
  另外我們也會看到下圖的Zero padding是1，也就是在輸入元素的周圍補了一圈0
  
  • 如何計算\(a_{0,0,0}\)？
  • 如何計算\(a_{1,0,1}\)？
• 我們把卷積神經網絡中的『卷積』操作叫做互相關(cross-correlation)操作

結學

• 如何推導卷積層的前向傳播？

任務：實現卷積層的前向傳播

• 請實現卷積層的前向傳播？
  答：待實現的代碼為：ConvLayer, Filter，實現后的代碼為：ConvLayer_answer, Filter_answer
  這里我們可以使用類型驅動開發的方式寫代碼，實現順序為自頂向下、廣度優先遍歷。具體就是先實現forward函數的第一層抽象，并給出對應函數的空實現和類型定義，通過編譯；然后安裝廣度優先遍歷的順序實現每個對應函數的第一層、第二層。。。。。。
• 請運行卷積層的代碼，檢查前向傳播的輸出是否正確？
  答：在Test.init函數中，構造了輸入數據和Conv Layer；在Test.test函數中，進行了前向傳播并打印了結果。結果為兩個Feature Map，它的數據如下所示：

["f:",[
    [3,3,[6,7,5,3,-1,-1,2,-1,4]],
    [3,3,[2,-5,-8,1,-4,-4,0,-5,-5]]
    ]]

我們可以手動計算下\(a_{0,0,0}\)（注意：因為zeroPadding=1，所以要對inputs補一圈0），結果等于6，與輸出的結果相同，證明forward的實現是正確的

總結

• 請總結本節課的內容？
• 請回答開始的問題？

參考資料

• 零基礎入門深度學習 | 第四章：卷積神經網絡