真實感渲染:三角函數、向量和矩陣
大家好~本課程為“真實感渲染”的線上課程,從0開始,介紹相關的圖形學算法和數學基礎,給出詳細的數學推導、偽代碼和實現代碼,最終帶領大家開發出基于物理的渲染器
線上課程資料:
加QQ群,獲得ppt等資料,與群主交流討論:106047770
本系列文章為線上課程的復盤,每上完一節課就會同步發布對應的文章
本課程系列文章可進入索引查看:
真實感渲染系列文章索引
為什么要學習本課
- 如何在幾何上表示向量的加法?
- 如何在代數上計算向量的加法?
- 三角函數、向量、矩陣在圖形學中有哪些應用?
主問題:什么是三角函數
-
對直角三角形而言,下面的三角函數的值分別是多少?
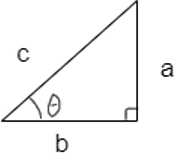
- sinθ
- cosθ
- tanθ
- cotθ
-
對任意三角形而言呢?
-
三角函數在圖形學中有哪些應用?
- 已知三角函數的值后,可以計算出角度:\(\arcsin\frac{1}{2} = 30^o\)
- 已知直角三角形的一邊和一個角度,可以計算另外一邊
主問題:什么是向量
-
用什么符號表示向量?
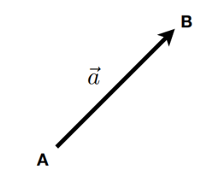
答:使用\(\overrightarrow{a}\)或者粗體a表示;
或者用起點和終點表示:\(\overrightarrow{AB} = B - A\) -
向量有什么特性?
答:具有方向和長度;
沒有絕對的起點; -
如何用代數表示向量?
答:
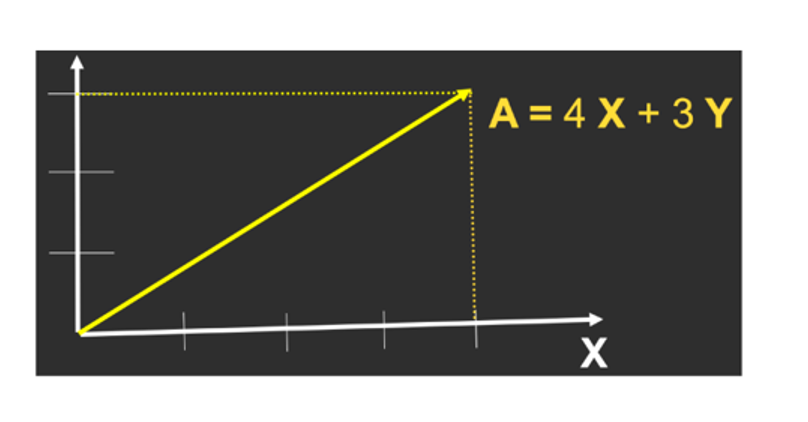
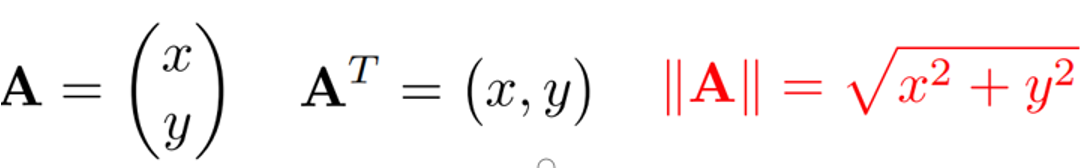
-
用什么符號表示向量的長度?
答:\(\Vert{\overrightarrow{a}}\Vert\) -
什么是單位向量?
答:長度為1的向量 -
如何計算一個向量的單位向量(向量正交化)?
答:\(\widehat{a}=\frac{\overrightarrow{a}} {\Vert{\overrightarrow{a}}\Vert}\) -
如何應用單位向量?
答:用來表示方向,如法線 -
如何計算向量的加法?
-
幾何上
答: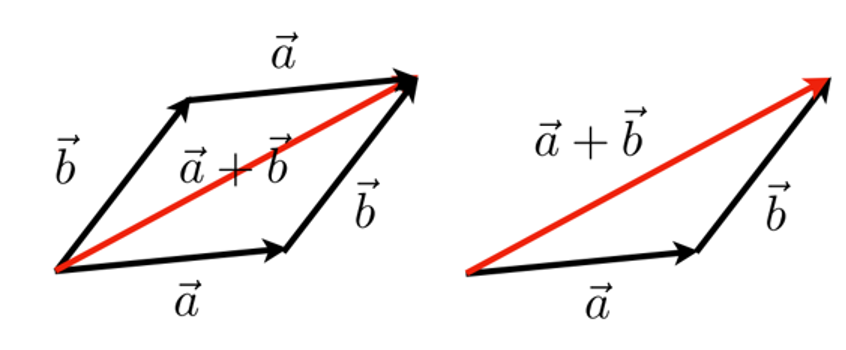
-
代數上
答:略
-
-
向量的點積的定義是什么?
答: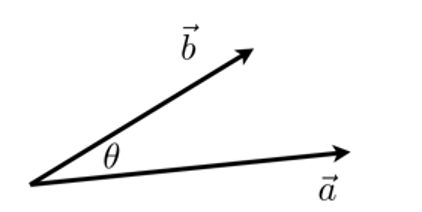
-
對于兩個單位向量,點積是多少?
答:\(\widehat{a} \cdot \widehat{{b}} = cos\theta\) -
點積滿足什么運算法則?
答: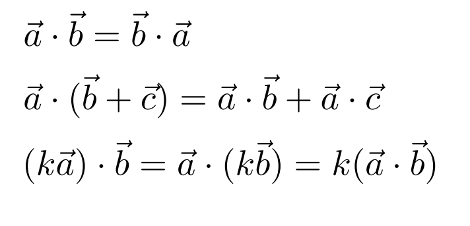
-
如何進行點積的代數運算?
答: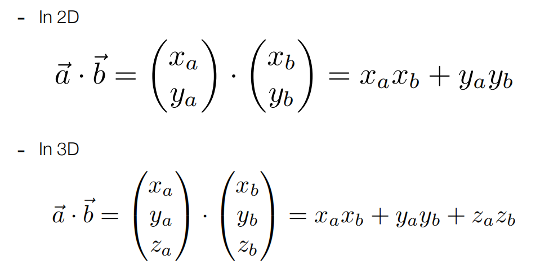
-
點積在圖形學中有哪些應用?
- 計算兩個向量的夾角
答:通過“兩個單位向量的點積”,得到\(cos\theta\),然后就可以得到夾角。這可以應用于計算光源方向和表面法線的夾角 - 計算一個向量到另一個向量的投影
答: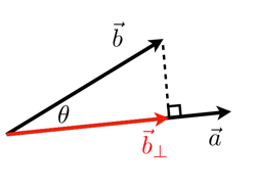

- 分解一個向量
答: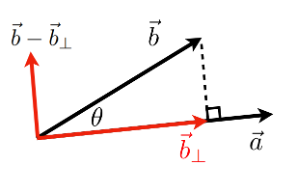
- 決定向量的前/后關系
答:
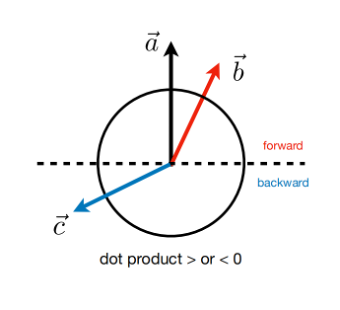
如上圖所示,如果兩個向量都在一個半圓內,則它們屬于“前”關系(如\(\overrightarrow{a},\overrightarrow{b}\));否則,則它們屬于“后”關系(如\(\overrightarrow{a},\overrightarrow{c}\))
如果兩個向量點積大于0,則\(cos\theta>0\),所以\(\theta \in [0, \frac{\pi}{2})\),它們屬于“前”關系;否則,它們屬于“后”關系
- 計算兩個向量的夾角
-
向量的叉積的定義是什么?
答:
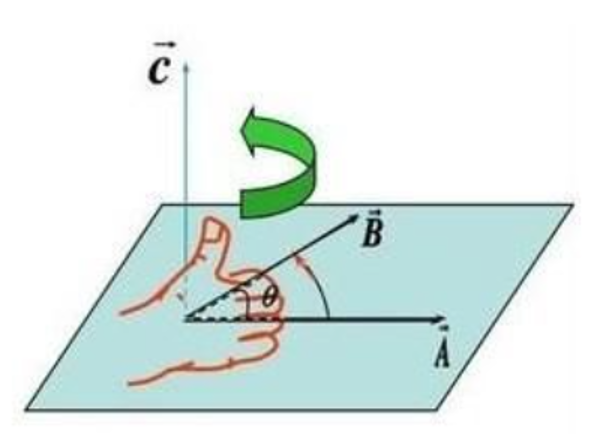
-
叉積滿足什么運算法則?
答: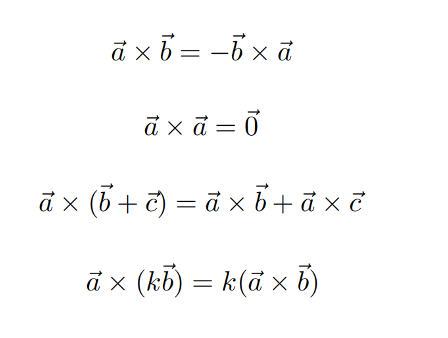
-
如何進行叉積的代數運算?
答: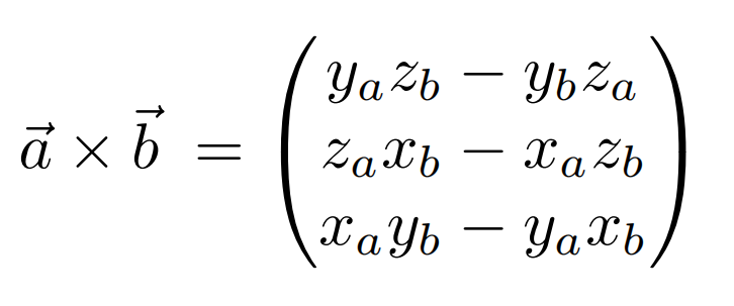
-
叉積在圖形學中有哪些應用?
- 構建坐標系
答: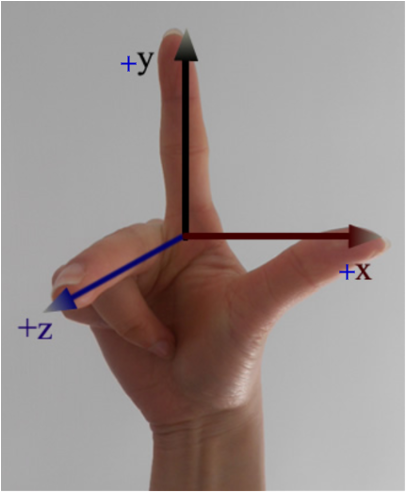
右手坐標系:
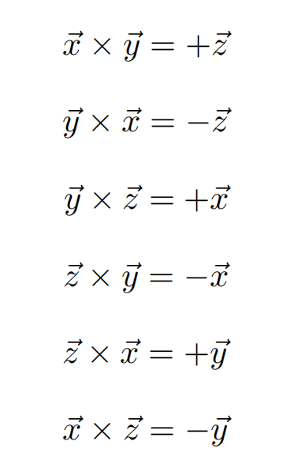
如上圖所示,通過兩個正交的單位向量的叉積來構建坐標系第三維的向量 - 決定向量的左/右關系
答: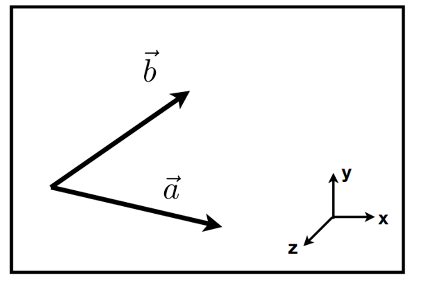
如上圖所示,假設\(\overrightarrow{a}, \overrightarrow{b}\)在xy平面,如果\(\overrightarrow{a} \times \overrightarrow{b} = +\overrightarrow{z}\),則\(\overrightarrow{b}在\overrightarrow{a}\)的左側;否則在右側 - 判斷一個點是否在三角形內
答:
分別判斷上圖的AB和AP、BC和BP、CA和CP,如果它們叉乘的結果同號,則點在三角形內。
- 構建坐標系
結學
- 什么是向量?
- 向量有什么特性?
- 點積在圖形學中有哪些應用?
- 叉積在圖形學中有哪些應用?
主問題:什么是矩陣
-
在圖形學中,矩陣有哪些應用?
答:用于坐標變換,如位移、旋轉、縮放 -
什么是矩陣?
答:可以看成是一個包含數字的數組


-
如何進行矩陣與標量相乘的代數計算?
答:矩陣的每個元素乘以該標量 -
“矩陣與矩陣”相乘有什么約束?
答: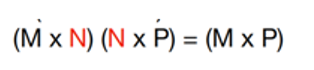
-
如何進行矩陣與矩陣相乘的代數計算?
答: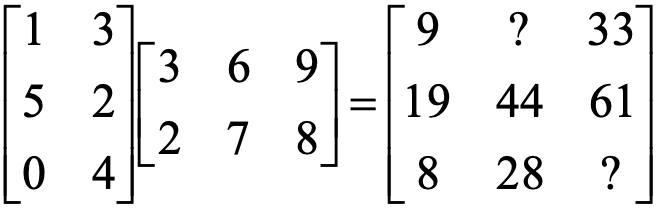
乘積中的第(i, j)個元素=第一個矩陣的第i行與第二個矩陣的第j列的點積 -
矩陣與矩陣相乘滿足什么運算法則?
答:不滿足交換律;
滿足結合律和分配律:
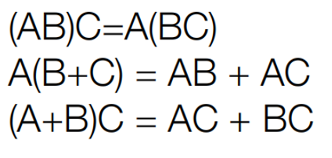
-
“矩陣與向量”相乘有什么約束?
答:矩陣(mxn)乘以向量(nx1) -
如何進行矩陣與向量相乘的代數計算?
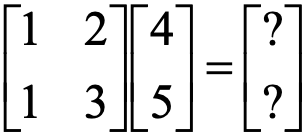
-
“矩陣與向量相乘”在圖形學中有哪些應用?
- 變換一個點
答:如將一個點沿y軸鏡像變換:
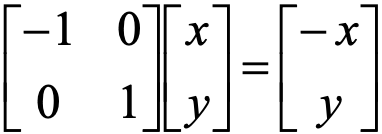
- 變換一個點
-
什么是矩陣轉置?
答: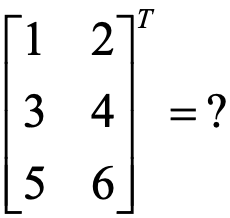
-
矩陣轉置滿足什么運算法則?
答: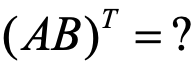
-
什么是單位矩陣?
答: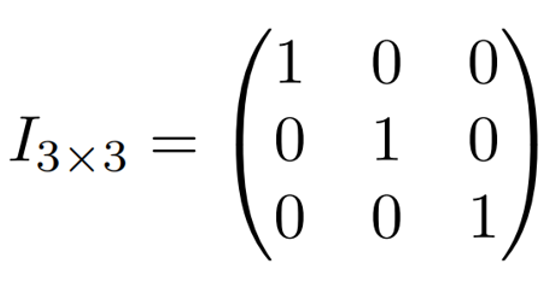
-
什么是逆矩陣?
答:
-
如何用矩陣表示向量的點積?
答: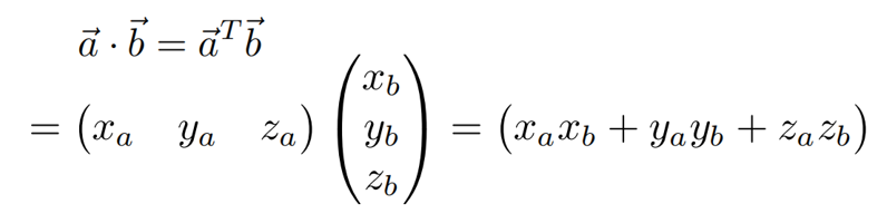
-
如何用矩陣表示向量的叉積?
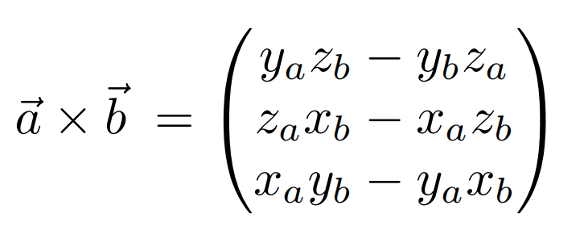
答:
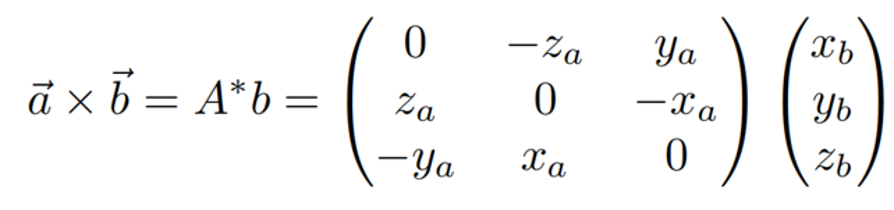
結學
- 什么是矩陣?
- “矩陣與向量相乘”在圖形學中有哪些應用?
總結
- 回答開始的問題?




 浙公網安備 33010602011771號
浙公網安備 33010602011771號