深度學習基礎課：使用交叉熵損失函數和Softmax激活函數（下）

大家好~本課程為“深度學習基礎班”的線上課程，帶領同學從0開始學習全連接和卷積神經網絡，進行數學推導，并且實現可以運行的Demo程序

線上課程資料：
本節課錄像回放

加QQ群，獲得ppt等資料，與群主交流討論：106047770

本系列文章為線上課程的復盤，每上完一節課就會同步發布對應的文章

本課程系列文章可進入索引查看：
深度學習基礎課系列文章索引

主問題：如何加快多分類的訓練速度？
- 結學
任務：識別手寫數字使用交叉熵損失函數和softmax激活函數
任務：改進代碼
總結
參考資料
謝謝你~

主問題：如何加快多分類的訓練速度？

“識別手寫數字“屬于單分類還是多分類？
答：多分類
“識別手寫數字“是否能使用單分類中的交叉熵損失函數？
答：不能
為什么？
答：

\[\begin{aligned} \frac{dE}{dw_{kj}} &=\delta_k a_j \\ &= \frac{dE}{dy_k}\frac{df(net_k)}{dnet_k} a_j \\ \end{aligned} \]

因為目前的交叉熵損失函數是在單分類下推導的。
而在多分類下，由于原有的激活函數不再適合，需要更換新的激活函數，導致上面公式中的\(\frac{df(net_k)}{dnet_k}\)發生了變化，導致損失函數E也需要改變，
所以需要新的損失函數

輸出層原來的sigmoid激活函數是否適用于多分類的情況？
答：不適用
輸出層需要新的激活函數
如何設計新的激活函數？
- 我們現在用a表示激活函數的輸出值
- 激活函數要滿足什么條件？
  答： \( a_k \in [0.0, 1.0] 以及 \sum_{k=1}^n a_k= 1 \)
- 你能設計一個滿足該條件的激活函數嗎？
  答：\(a_k = \frac{t_k}{\sum_{i} t_i} 且t_i(包括t_k) >0.0\)
我們使用softmax激活函數，它的公式為：
答： \( a_k = \frac{e^{net_k}}{\sum_{i=1}^n e^{net_i}} \)
為什么\(t_k\)使用\(e^k\)這種函數呢？這可能是因為它大于0.0；并且由于是非線性的所以值的間隔拉的比較開，從而能適應更多的變化
softmax是否滿足條件？
答：滿足
我們現在用y表示真實值（即標簽）
如何計算loss？
答：\( \overrightarrow{loss} = \overrightarrow{a_{輸出層}} - \overrightarrow{y} \)
如何參考設計單分類誤差項公式的思路來設計多分類誤差項的公式，使其滿足loss與誤差項成正比？
答：\( \overrightarrow{\delta_{輸出層}} =\overrightarrow{loss} = \overrightarrow{a_{輸出層}} - \overrightarrow{y} \)
我們需要將單分類的交叉熵損失函數修改一下，使其滿足什么公式？
答：為了簡單，我們暫時不考慮誤差項向量，而只考慮單個神經元的誤差項。所以應該滿足下面的公式：
\( E = ?從而 \sum_{i=1}^n \frac{dE}{da_i} \frac{da_i}{dnet_k}=\delta_k =a_k - y_k \)
（注意：因為每個a的計算都有所有的net參加，所以要使用全導數公式進行累加）
現在直接給出修改后的交叉熵損失函數的公式： \(E = - \sum_{j=1}^n y_j \ln a_j \\\)
請根據修改后的損失函數和softmax激活函數公式，推導誤差項，看下是否為設計的公式： \( \delta_k =\sum_{i=1}^n \frac{dE}{da_i} \frac{da_i}{dnet_k}= ?(應該為a_k - y_k) \)

答：

\(\because\)

\[\begin{aligned} \frac{dE}{da_i} &= \frac{d- \sum_{j=1}^n y_j \ln a_j }{da_i} &= - \frac{y_i}{a_i} \end{aligned} \]

\(\therefore\)

\[\begin{aligned} \delta_k &= \sum_{i=1}^n \frac{dE}{da_i} \frac{da_i}{dnet_k} \\ &= - \sum_{i=1}^n \frac{y_i}{a_i} \frac{da_i}{dnet_k} \\ \end{aligned} \]

因為只能有一個真實值為1，所以假設\(y_j=1\)，其它\(y_i=0\)，則

\[\begin{aligned} \delta_k &= - \frac{1}{a_j} \frac{da_j}{dnet_k} \\ \end{aligned} \]

現在需要推導\(\frac{da_j}{dnet_k}\)，推導過程如下：

因為\(a_j\)可以看作是\(net_j\)的復合函數：

\[ a_j =\frac{e^{net_j}}{\sum_{m=1}^n e^{net_m}} = f(e^{net_j}, \sum_m e^{net_m}) \\ \]

所以：

\[\frac{da_j}{dnet_k} = \frac{da_j}{de^{net_k}} \frac{de^{net_k}}{dnet_k} + \frac{da_j}{d\sum_m e^{net_m}} \frac{d\sum_m e^{net_m}}{dnet_k} \\ \]

現在分兩種情況：

若 k = j

\[\frac{da_j}{dnet_k} = \frac{da_j}{dnet_j} = \frac{da_j}{de^{net_j}} \frac{de^{net_j}}{dnet_j} + \frac{da_j}{d\sum_m e^{net_m}} \frac{d\sum_m e^{net_m}}{dnet_j} \\ \]

\(\because\)

\[ \begin{aligned} \frac{da_j}{de^{net_j}} &= \frac{1}{\sum_j e^{net_j}} \\ \frac{de^{net_j}}{dnet_j} &= e^{net_j}\\ \frac{da_j}{d\sum_m e^{net_m}} &= - \frac{e^{net_j}}{(\sum_m e^{net_m})^2} \\ \frac{d\sum_m e^{net_m}}{dnet_k} &= \frac{d\sum_m e^{net_m}}{de^{net_k}} \frac{de^{net_k}}{dnet_k} = e^{net_k} \\ \end{aligned} \]

\(\therefore\)

\[ \frac{da_j}{dnet_k} = \frac{da_j}{dnet_j} = a_j(1-a_j) \]

若 k \(\neq\) j

\[\frac{da_j}{dnet_k} = \frac{da_j}{de^{net_k}} \frac{de^{net_k}}{dnet_k} + \frac{da_j}{d\sum_m e^{net_m}} \frac{d\sum_m e^{net_m}}{dnet_k} \\ \]

\(\because\)

\[ \begin{aligned} \frac{da_j}{de^{net_k}} &= 0 \\ \frac{da_j}{d\sum_m e^{net_m}} &= - \frac{e^{net_j}}{(\sum_m e^{net_m})^2} \\ \frac{d\sum_m e^{net_m}}{dnet_k} &= e^{net_k} \\ \end{aligned} \]

\(\therefore\)

\[ \frac{da_j}{dnet_k} = -a_j a_k \]

經過上面的推導后，寫成向量的形式就是：

\[ \overrightarrow{\delta_{輸出層}} = \begin{bmatrix} - \frac{1}{a_j} \cdot (-a_j a_1) \\ \vdots \\ - \frac{1}{a_j} \cdot (a_j(1-a_j)) \\ \vdots \\ - \frac{1}{a_j} \cdot (-a_j a_n) \\ \end{bmatrix} = \begin{bmatrix} a_1 \\ \vdots \\ a_j - 1 \\ \vdots \\ a_n \\ \end{bmatrix} = \overrightarrow{a_{輸出層}} - \overrightarrow{y} \\ \]

結學

如何加快多分類的訓練速度？
根據交叉熵損失函數和softmax，推導誤差項的過程是什么？

任務：識別手寫數字使用交叉熵損失函數和softmax激活函數

請在“識別手寫數字Demo”中使用交叉熵損失函數和softmax激活函數，并且加入“通過打印loss來判斷收斂”
答：待實現的代碼為：NewCross_softmax，實現后的代碼為：NewCross_softmax_answer
請每個同學運行代碼
- 剛開始訓練時，有什么警告？
  答：如下圖所示：有“輸出層梯度過大”的警告
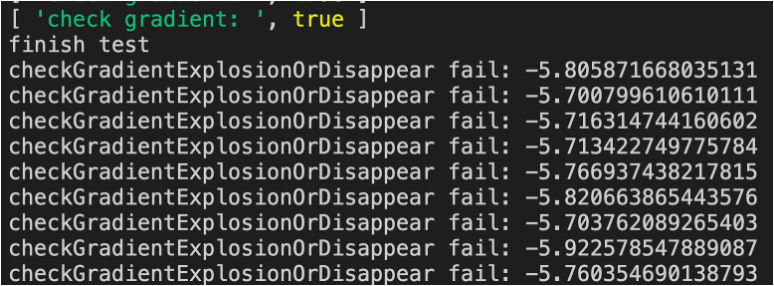
- 注釋掉警告代碼后，看下loss的訓練速度與之前的代碼相比是否明顯加快？
  答：沒有

任務：改進代碼

找到發生警告的原因？
答：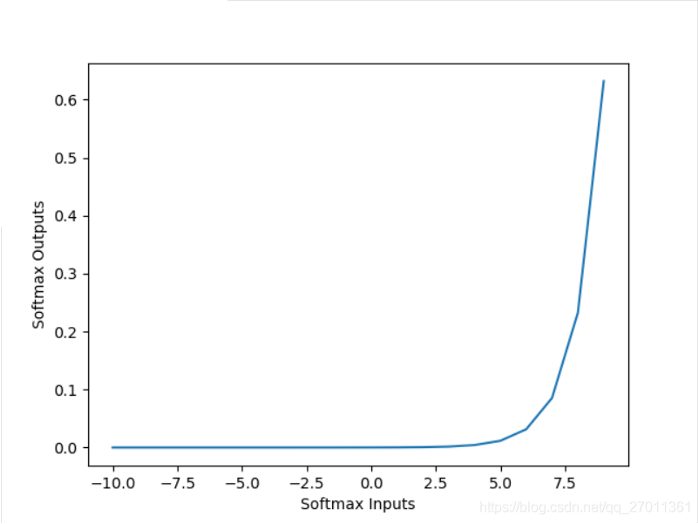
因為輸出層加權和沒有做縮小處理，所以加權和比較大（范圍為[10.0,15.0]左右）。
通過上圖(softmax的圖像)可知，該范圍內的梯度很大，所以報“梯度爆炸”的警告
如何改進代碼？
答：將輸出層的學習率變小為0.1
將輸出層的學習率分別變小為1.0、0.1，運行代碼，看是否解決了警告，并提升了訓練速度？
答：變小為0.1后運行代碼的結果如下圖所示：

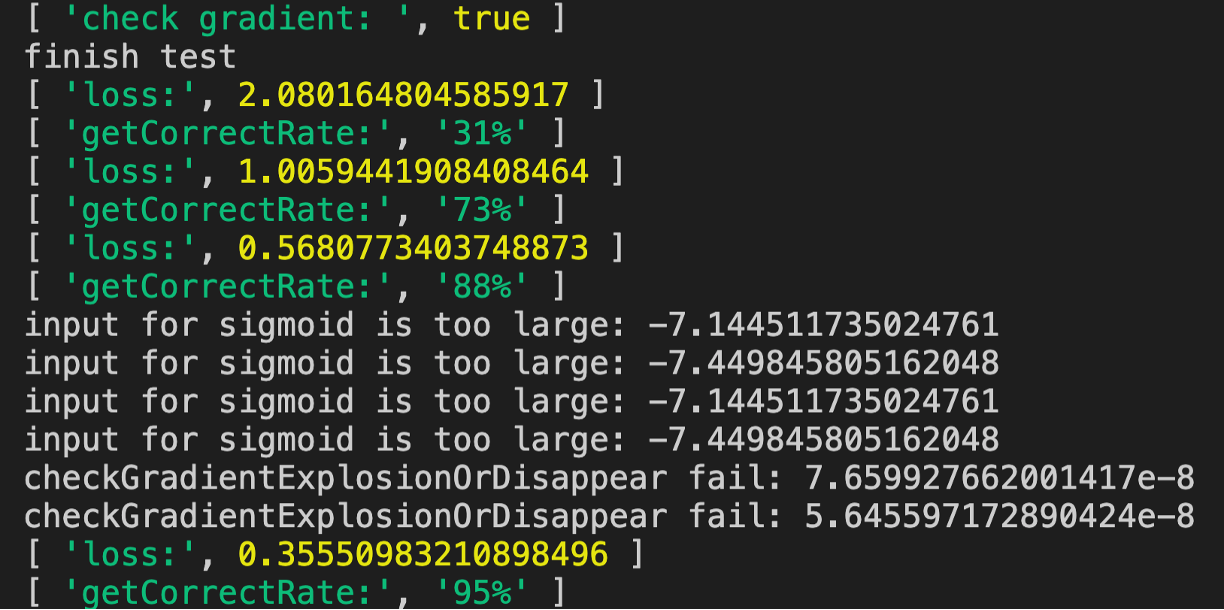
我們看到只需要四輪訓練既達到95%的正確率
那么為什么在正確率到88%后會開始報輸出層的一些梯度值過小的警告呢？這是因為此時loss小，所以梯度也小了