深度學習基礎課：全連接層的前向和后向傳播推導（下）

大家好~我開設了“深度學習基礎班”的線上課程，帶領同學從0開始學習全連接和卷積神經網絡，進行數學推導，并且實現可以運行的Demo程序

線上課程資料：
本節課錄像回放1
本節課錄像回放2
本節課錄像回放3

加QQ群，獲得ppt等資料，與群主交流討論：106047770

本系列文章為線上課程的復盤，每上完一節課就會同步發布對應的文章

本文為第三節課：“全連接層的前向和后向傳播推導（下）”的復盤文章

本課程系列文章可進入索引查看：
深度學習基礎課系列文章索引

回顧相關課程內容
主問題：如何推導全連接層的后向傳播？
- 為什么要推導全連接層的后向傳播？
- 主問題：如何推導全連接層的后向傳播？
任務：實現全連接層的后向傳播
任務：使用全連接層實現“判斷性別Demo”
總結
參考資料

回顧相關課程內容

第二節課“判斷性別”Demo需求分析和初步設計（下1）
- 損失函數的表達式是什么？
- 隨機梯度下降算法是什么？
- 隨機梯度下降公式是什么？
- 求損失函數的極小值點的梯度下降公式是什么？
第二節課“判斷性別”Demo需求分析和初步設計（下2）
- 對于“判斷性別”的Demo，??可以是什么函數？
- 什么是訓練?
- 如何求梯度？
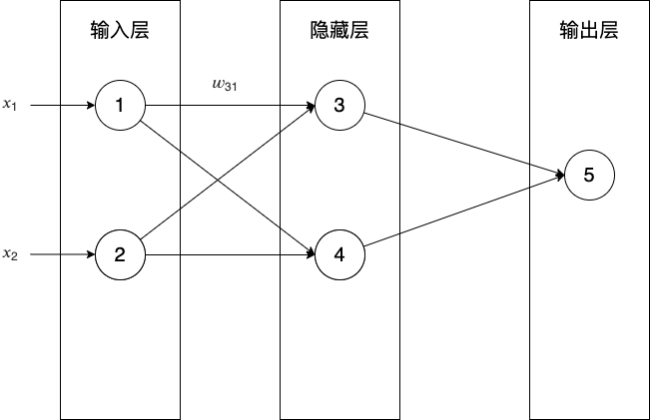
  - 如何求\(\frac{dE}{dw_{53}}\)？
  - 如何求\(\frac{dE}{dw_{31}}\)？

主問題：如何推導全連接層的后向傳播？

為什么要推導全連接層的后向傳播？

通過訓練，我們希望得到什么？
為了得到更新后的權重和偏移，需要知道什么？
“判斷性別Demo”是如何實現訓練的？
梯度的數量太多，導致計算很臃腫，如何優化？
如果增加隱藏層中的神經元數量，是否會修改梯度計算的代碼？
如何才能不修改代碼，只調整參數即可？

答：將梯度向量化

回顧計算梯度的代碼，有哪些是重復的計算？
能否在梯度向量化公式中，將重復計算提出來？

答：參考一文搞懂反向傳:

其實對于已經計算完畢的節點我們完全可以直接拿來用，因此我們可以重新看待這個問題，從后往前更新。先更新后邊的權重，之后再在此基礎上利用更新后邊的權重產生的中間值來更新較靠前的參數。
這個中間變量就是本課要引入的誤差項

因此，我們需要先計算出輸出層的誤差項；
再根據它來計算出隱藏層的誤差項；
最后根據它們分別計算出輸出層和隱藏層的梯度

主問題：如何推導全連接層的后向傳播？

輸出層神經元的誤差項是什么？
答：
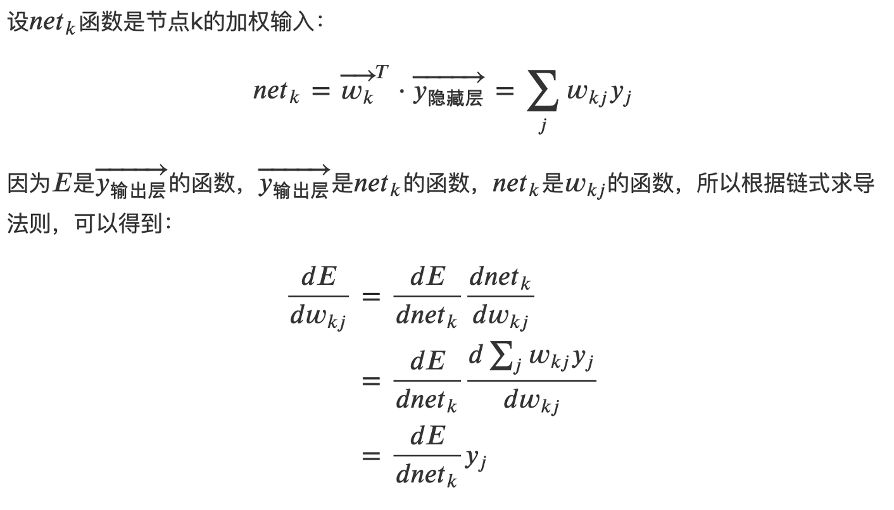
隱藏層神經元的誤差項是什么？
答：
所以每層神經元的誤差項計算公式都是什么？
答：

\[\delta_j=\frac{dE}{dnet_j} \]

每個神經元權重\(??_{ji}\)的梯度（ \(??_{ji}\)表示從神經元i接到神經元j的權重）是什么？
答：

\[\frac{dE}{dw_{ji}}=\delta_j a_i\\ 其中a_i為神經元i的輸出 \]

所以求梯度的問題轉換為求什么？
答：求誤差項
如何計算輸出層神經元的誤差項： \(\delta_k=\frac{dE}{dnet_k}\) ？
答：
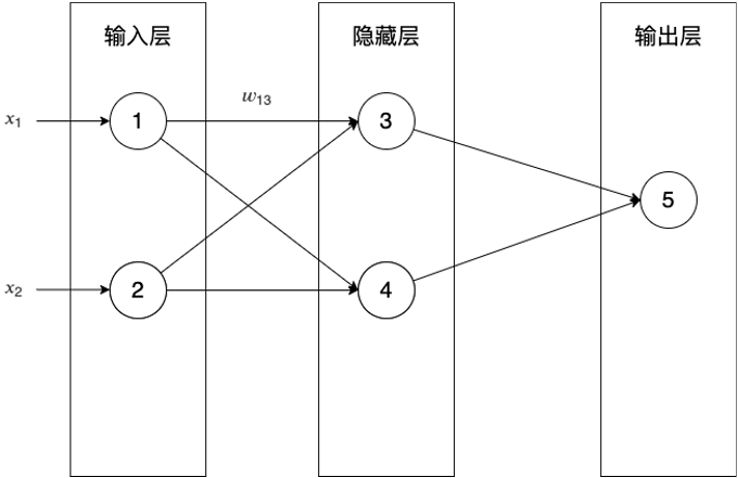
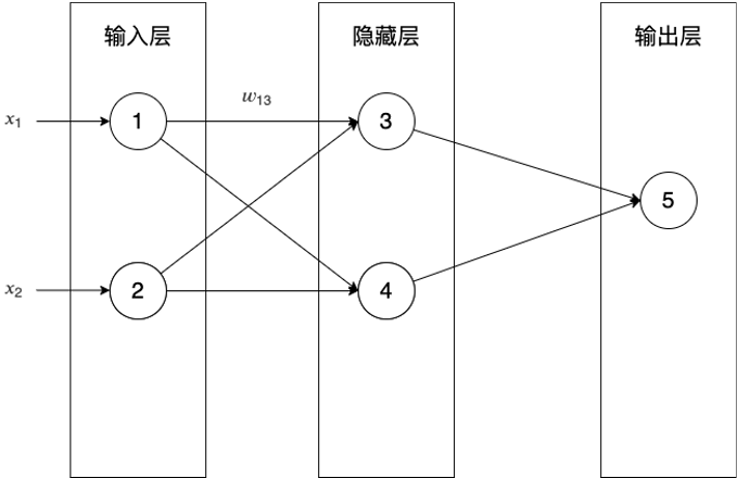
對于下圖的神經網絡，輸出層的誤差向量是什么？

答：

\[\overrightarrow{\delta_{輸出層}} = \begin{bmatrix} \delta_{5} \\ \end{bmatrix} \]

如何計算隱藏層神經元的誤差項： \(\delta_j=\frac{dE}{dnet_j}\) ？
答：
對于下圖的神經網絡，隱藏層的誤差向量是什么？

答：

\[\begin{aligned} W_{輸出層} &=\begin{bmatrix} w_{53}, w_{54}, w_{b_5} \\ \end{bmatrix} \\ \overrightarrow{\delta_{隱藏層}} &=\begin{bmatrix} \delta_{3} \\ \delta_{4} \\ \end{bmatrix}\\ &= \begin{bmatrix} \overrightarrow{\delta_{輸出層}} \cdot W_{輸出層_{1列}} \;\; \frac{df(net_3)}{dnet_3} \\ \overrightarrow{\delta_{輸出層}} \cdot W_{輸出層_{2列}} \;\; \frac{df(net_4)}{dnet_4} \\ \end{bmatrix} \end{aligned} \]

該向量公式同樣適用于輸出層有多個神經元的情況

更新后的輸出層和隱藏層的梯度下降算法是什么？
答：更新前的算法公式如下：

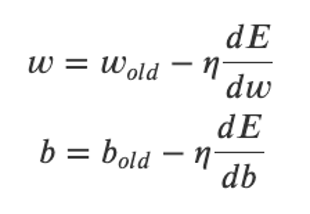
更新后的輸出層和隱藏層的算法公式如下：
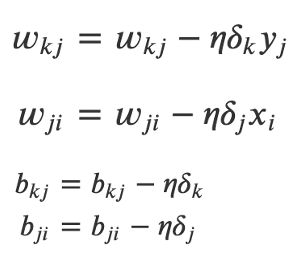
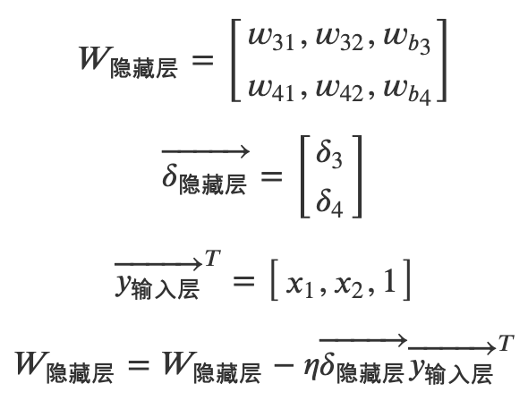
對于下圖的神經網絡，如何向量化輸出層和隱藏層的梯度下降算法？

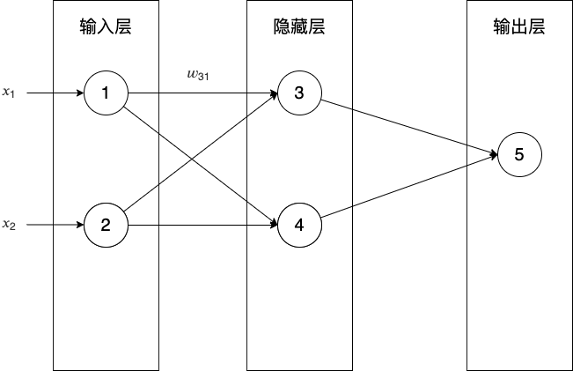
答：輸出層梯度下降算法向量化公式如下：

隱藏層梯度下降算法向量化公式如下：
什么是后向傳播算法？
答：先計算輸出層的誤差項，然后反向依次計算每層的誤差項直到與輸入層相連的層，最后根據每層的誤差項和輸入得到每層的梯度

任務：實現全連接層的后向傳播

請實現全連接層的后向傳播的代碼（損失函數和激活函數與判斷性別Demo一樣）
答：待實現的代碼：NeuralNetwork_train
實現后的代碼：NeuralNetwork_train_answer
使用判斷性別Demo的神經網絡結構，運行代碼，通過運行測試

答：因為NeuralNetwork_train_answer->train函數打印的loss的結果與判斷性別Demo的NeuralNetwork_train_before->train函數打印的loss一樣，所以說明代碼正確，通過了運行測試

任務：使用全連接層實現“判斷性別Demo”

請參考判斷性別Demo的代碼NeuralNetwork_train_fix_zeroMean_answer_fix，整合全連接層的前向、后向傳播的代碼
答：待實現的代碼：LinearLayer
實現后的代碼：LinearLayer_answer
使用判斷性別Demo的神經網絡結構，運行代碼，通過“判斷性別Demo”的運行測試

答：運行代碼LinearLayer_answer，運行結果是loss收斂，并且正確地推理出兩個樣本的性別，從而通過了運行測試