1.流程

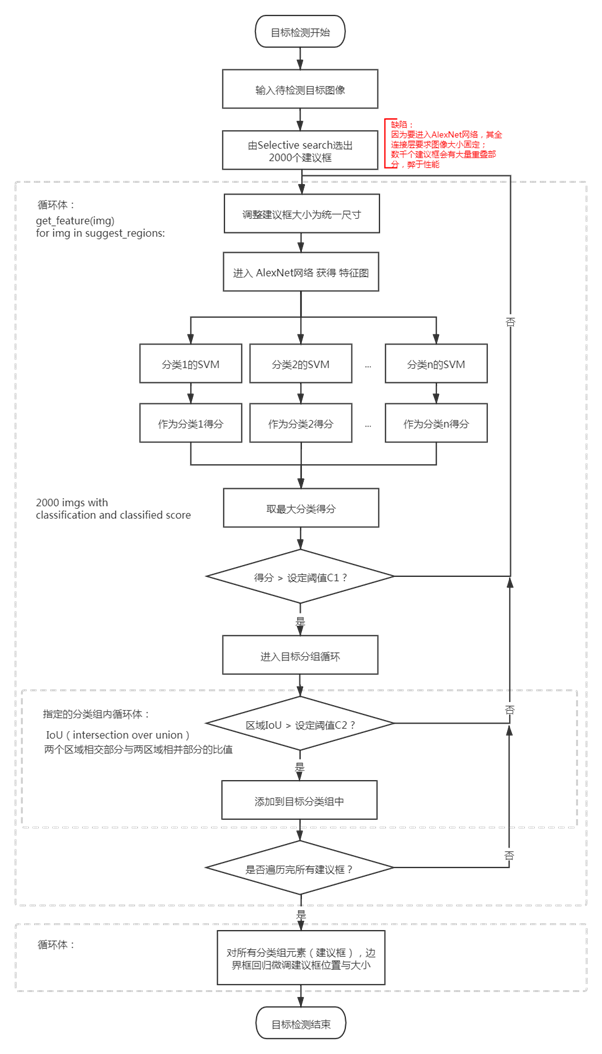
為什么要用SVM而不是CNN最后一層的softmax？

取什么模型必然是有標(biāo)準(zhǔn)衡量，這個(gè)流程取得是書上[4]寫的，作者說他得實(shí)驗(yàn)證明SVM比FC的mAP要高，所以我流程暫且這樣畫了。

R-CNN取的是alexNet的遷移學(xué)習(xí)進(jìn)行微調(diào)，它原來的訓(xùn)練數(shù)據(jù)就是隨機(jī)的，而為了避免正樣本數(shù)據(jù)過小導(dǎo)致卷積網(wǎng)絡(luò)過擬合，正樣本的框中沒有SVM訓(xùn)練時(shí)嚴(yán)格，

也即說，訓(xùn)練中，相同的數(shù)據(jù)，在SVM里正樣本卡得更嚴(yán)格，讓SVM判別是正樣本的概率也會低一些，那SVM的mAP高一些也能理解。

那么又有一個(gè)新問題，既然alexNet后接softmax結(jié)果不理想，那用fc+softmax替代svm呢？這個(gè)討論在下節(jié)。 

（剛好有一個(gè)圖說明這個(gè)mAP怎么算，它更關(guān)注在確實(shí)有目標(biāo)的建議框里面，模型給出的“信心”是多少）

引自：https://blog.csdn.net/asasasaababab/article/details/79994920

2.數(shù)學(xué)概念

SVM（Support Vector Machines），主要想找到分離一批數(shù)據(jù)的超平面，約定是，找到距離這個(gè)超平面最近的點(diǎn)做距離該點(diǎn)最遠(yuǎn)的線（/面）。

支持向量（support vecotr）就是離超平面最近的點(diǎn)，SVM由此命名。

而規(guī)劃超平面涉及到核（Kernal）函數(shù)概念，最終計(jì)算SVM會是解決不等式約束問題，這里面就有多種方式。

（原始的SVM僅用于二分類，分類標(biāo)簽按計(jì)算需求確定，可能是0和1，或者是-1和1，以此區(qū)分兩個(gè)類別。多種分類需要動刀函數(shù)距離）

對于一個(gè)二維平面來說，如果能用一條直線區(qū)分出兩批數(shù)據(jù)，那么如何確定這條直線呢（可能會有多條），

SVM原則是找到兩批數(shù)據(jù)中點(diǎn)距離目標(biāo)線最近的點(diǎn)，距離最大的解。這聽起來有很多個(gè)未知數(shù)

已知點(diǎn)A，假設(shè)超平面表達(dá)式（目標(biāo)函數(shù)）為 ，那么點(diǎn)A對y的距離（推導(dǎo)過程讓人腦閉，有需要再深究）：

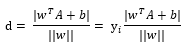
這個(gè)yi是取-1和1的標(biāo)簽值，注，yi的i不同書寫在了不同位置（上標(biāo)或下標(biāo)），但都是表示標(biāo)簽。

為了下文計(jì)算方便，把分子拎出來，為了掉絕對值，此處添加變量yi（表示標(biāo)簽值，i = 1,2,3,..n，表示第幾個(gè)數(shù)據(jù)）[2]， 

yi取-1或1，以使分子結(jié)果不變，

設(shè)定下式為函數(shù)距離（或稱為函數(shù)間隔），可以表示點(diǎn)到超平面的距離遠(yuǎn)近。

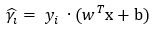
目標(biāo)是找到函數(shù)距離最小值，

下一步是求距離超平面最近的點(diǎn)對超平面的距離最大化之解：

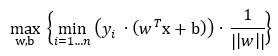
優(yōu)化問題，分成兩個(gè)整體來處理，

已知要求的函數(shù)間隔最小，那么有：

整理一下，

又  不影響margin取值，此處可令其為1，（？[2]筆者并不太明白），

求||w||最小值等價(jià)于||w||2/2的最小值，為了求導(dǎo)方便，上式可轉(zhuǎn)化為：

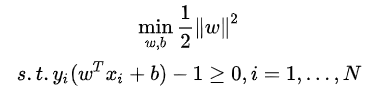
為了求解線性可分支持向量機(jī)的最優(yōu)化問題，將它作為原始最優(yōu)化問題，

應(yīng)用拉格朗日對偶性，通過求解對偶問題(dual problem)得到原始問題(primal problem)的最優(yōu)解，這就是線性可分支持向量機(jī)的對偶算法，

這樣做的優(yōu)點(diǎn)：一是對偶問題往往更容易求解；二是自然引入核函數(shù)，進(jìn)而推廣到非線性分類問題。

——《統(tǒng)計(jì)學(xué)習(xí)方法》

關(guān)于如何求解拉格朗日此處不敘述，詳見[2][3]，

拉格朗日乘數(shù)法式子：

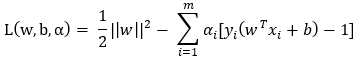
省略化簡，得到約束：

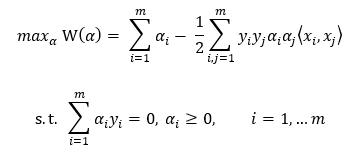
注，尖括號表示向量內(nèi)積（也即點(diǎn)積）。

由于此時(shí)假設(shè)數(shù)據(jù)100%線性可分，然而真實(shí)數(shù)據(jù)并不都是那么“干凈”，此處引入松弛變量（slack variable），以允許有些數(shù)據(jù)點(diǎn)處于分隔面錯(cuò)誤的一側(cè)，約束條件變?yōu)椋篊≥α ≥ 0 ，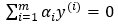

如何求解，傳統(tǒng)地有二次規(guī)劃求解（quadratic solver），但是這個(gè)計(jì)算量大，John Platt發(fā)布了一個(gè)叫SMO（Sequential Minimal Optimization，序列最小優(yōu)化）的算法以減少計(jì)算。

簡化的SMO偽代碼：

創(chuàng)建一個(gè)α向量并將其初始化為0的向量

當(dāng)?shù)螖?shù)小于最小迭代次數(shù)時(shí)（外循環(huán)）：

對數(shù)據(jù)集中的每個(gè)數(shù)據(jù)向量（內(nèi)循環(huán)）：

　　如果該數(shù)據(jù)向量可以被優(yōu)化：

　　　　隨機(jī)選擇另外一個(gè)數(shù)據(jù)向量

　　　　同時(shí)優(yōu)化這兩個(gè)向量

　　　　如何這兩個(gè)向量不能被同時(shí)優(yōu)化，退出內(nèi)循環(huán)

如果所有向量都沒被優(yōu)化，增加迭代數(shù)目，繼續(xù)下一次循環(huán)

核（kernel）函數(shù)

如果一批數(shù)據(jù)并沒有呈現(xiàn)明顯的直線劃分規(guī)律，例如呈現(xiàn)環(huán)分布的劃分規(guī)律，

那么求解這個(gè)低緯度的非線性問題，最好就把它轉(zhuǎn)化成高緯度的線性問題，前者轉(zhuǎn)化到后者，這個(gè)映射過程用核函數(shù)滿足。

因?yàn)镾VM的向量都是內(nèi)積表示，這里面把內(nèi)積運(yùn)算替換成核函數(shù)的方式，就叫做核技巧（kernel trick）或核變電（kernel substation）。

徑向基核函數(shù)（Radial Basis Function），是某種沿徑向?qū)ΨQ的標(biāo)量函數(shù)，是一個(gè)常用的度量兩個(gè)向量距離的核函數(shù)。

例如，線性問題，是 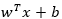，非線性問題，假設(shè)核函數(shù)取徑向基函數(shù)的高斯版本：

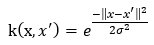
（？）其中，σ是用戶定義的用于確定到達(dá)率（reach）或者說函數(shù)值跌落到0的速度參數(shù)。

def kernelTrans(X, A, kTup):
  m,n = shape(X)
  K = mat(zeros((m, 1)))
  if kTup[0] == 'lin' : K = X*A.T
  elif kTup[0] == 'rbf' :
      for j in range(m):
          deltaRow = X[j, :] – A  # 公式
          K[j] = deltaRow*deltaRow.T  # 平方
      K = exp(K / (-1*kTup[1]**2))  # 元素間的除法
  else : raise NameError('That Kernel is not recognizaed~ ')
  return K

class optStruct:
  def __init__(self, dataMatIn, classLabels, C, toler, kTup):
      self.X = dataMatIn
      …
      self.m = shape(dataMatIn)[0]
      self.K = mat(zeros((self.m, self.m)))
      for i in range(self.m):
          self.K[:,i] = kernalTrans(self.X, self.X[i, :], kTup)

SVM用于數(shù)值型數(shù)據(jù)，可視化分割超平面，其主要求解在于兩個(gè)變量的調(diào)優(yōu)，幾乎所有分類問題都能用它，

原始的SVM是一個(gè)二分類器，應(yīng)對多類問題需要調(diào)整SVM，

但其核函數(shù)的選擇，以及核函數(shù)里自定義變量的影響，使得這個(gè)最優(yōu)解需要大量訓(xùn)練。

=======================================================

資料：

[1] https://baike.baidu.com/item/拉格朗日乘數(shù)法/8550443?fromtitle=拉格朗日乘子法

[2] https://zhuanlan.zhihu.com/p/146515617

[3] https://blog.csdn.net/m0_37687753/article/details/80964472?spm=1001.2014.3001.5501

[4]杜鵬、諶(chen2)明、蘇統(tǒng)華 編著《深度學(xué)習(xí)與目標(biāo)檢測》

Peter Harrington著《機(jī)器學(xué)習(xí)實(shí)戰(zhàn)》

https://blog.csdn.net/m0_37687753/article/details/80964487

https://blog.csdn.net/laobai1015/article/details/82763033

https://baike.baidu.com/item/函數(shù)間隔/23224467?fr=aladdin

按這個(gè)計(jì)算原理來說，如果有一份數(shù)據(jù)，代入到SVM的分隔面里，為0是在面上，如果值>0，是正分類，<0是負(fù)分類；

此處可以觀察到，如果值越大，即距離分隔面越遠(yuǎn)，那分類正確性也會越大。

如何改造SVM處理多種分類呢？

改造SVM為多分類識別：

1 直接法：在目標(biāo)函數(shù)上修改，將多個(gè)分類面的參數(shù)求解合并成一個(gè)最優(yōu)化問題，這種計(jì)算復(fù)雜，僅適合小型問題。

2 間接法：把多分類轉(zhuǎn)變成多個(gè)二分類問題，常見有one-against-one和one-against-all兩種。

資料：

http://blog.itpub.net/29829936/viewspace-2168864/

3.應(yīng)用代碼

筆者還沒有實(shí)現(xiàn)過，暫且擱置。