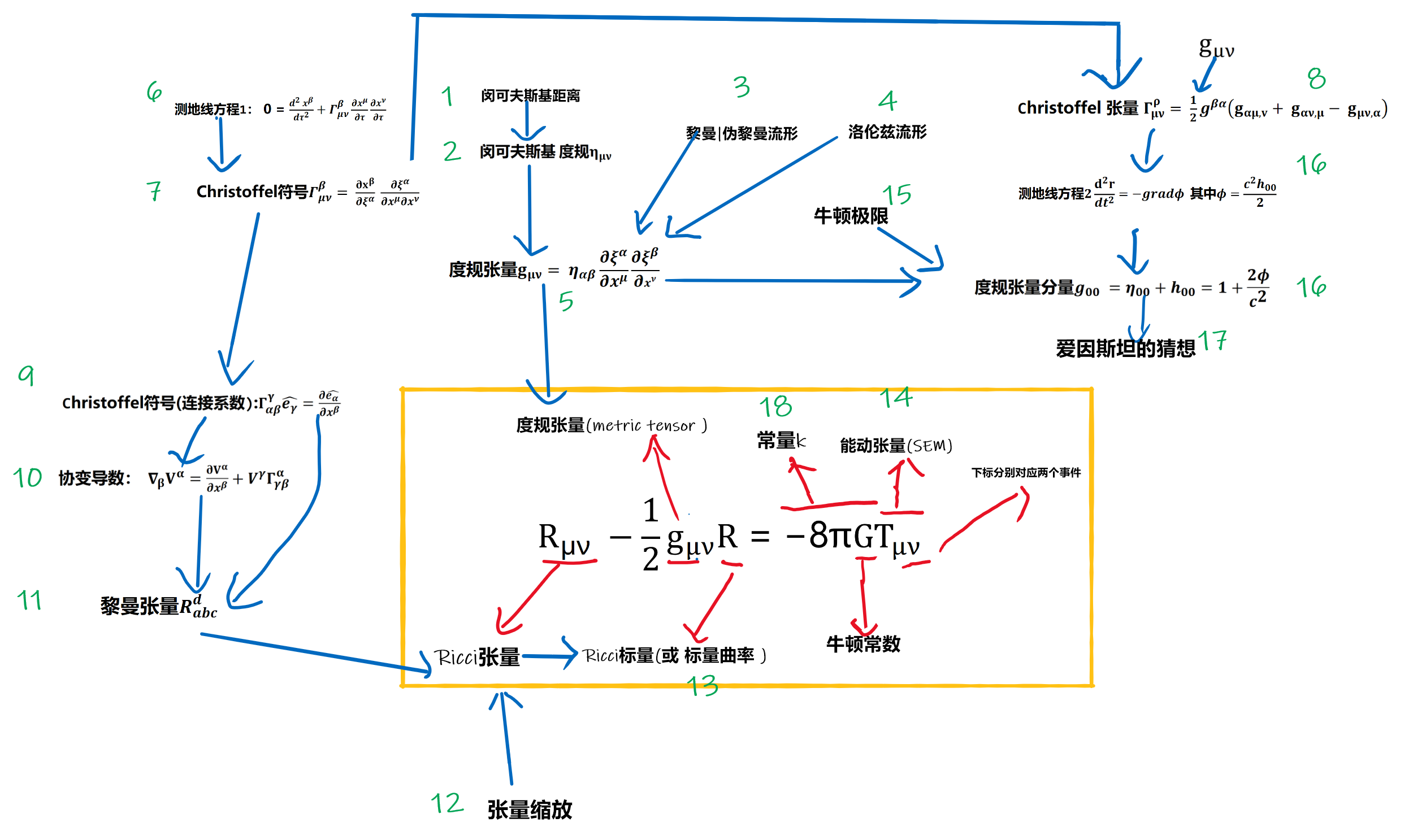
從狹義相對論洛倫茲變換到廣義相對論場方程的推導
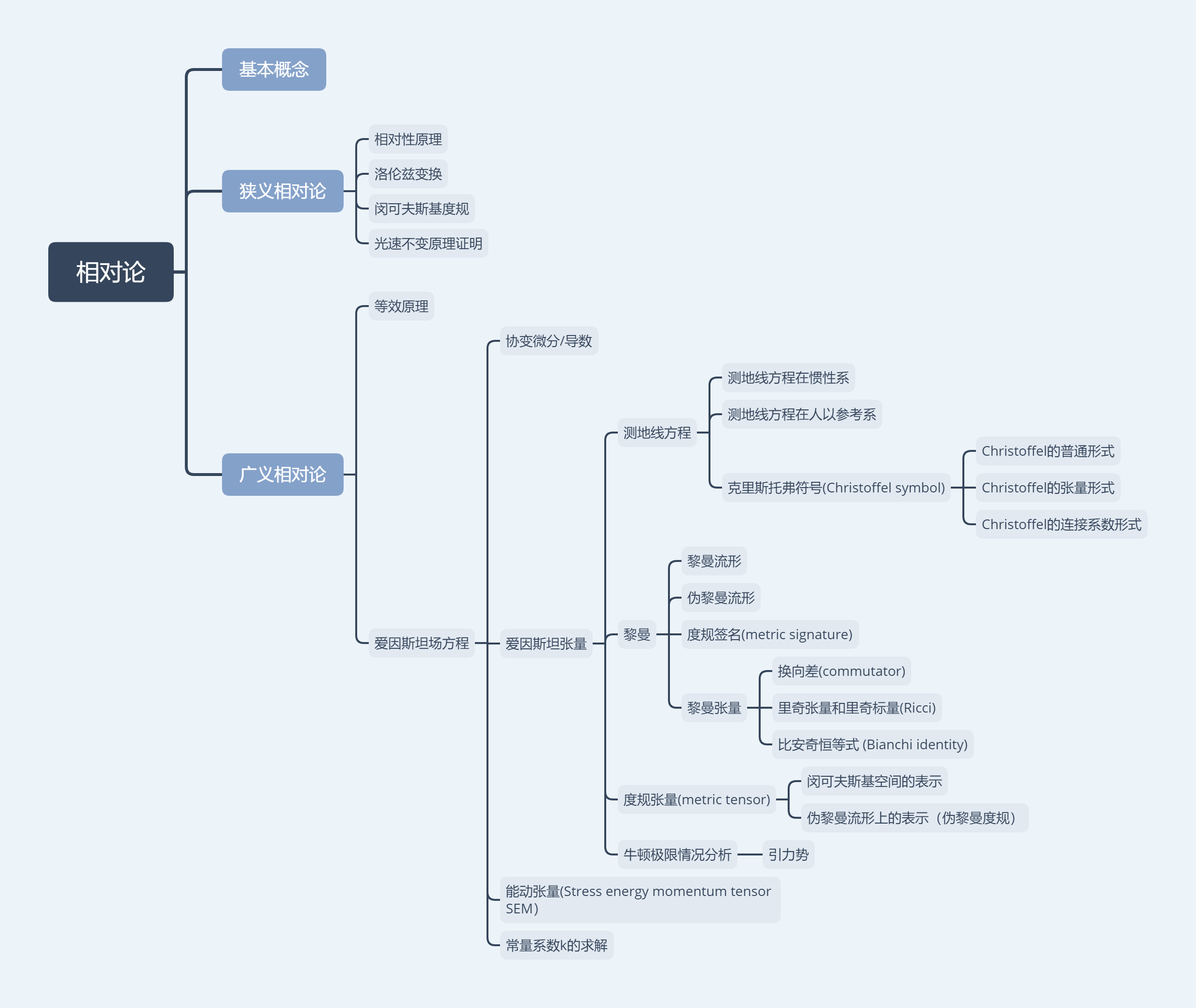
| 空間類型 | 空間曲率 | 平行線 | 三角形三內角之和 | 圓周率 | 例子 |
|---|---|---|---|---|---|
| 黎氏空間 | 正 | 無 | >180° | <π | 球面 |
| 歐式空間 | 零 | 一條 | =180° | =π | 平面 |
| 羅氏空間 | 負 | 無 | >=兩條以上 | >π | 偽球面,馬鞍面 |
我們稱這個符號為dummy index
$$ 連續出現兩次相同的符號,不強調他們是上標還是下標,都是滿足愛因斯坦取和原則的 $$$$- 只出現一次的稱為自由索引 $$$$- 但是注意不會出現三個相同的標記在同一項中 $$$$如x_{ii} \cdot y_{ji} 但是x_{ii}+y_{ji}卻是可以的 $$$$- 當同時出現上下標時,也表示他們的取和如 x^i_j = \sum_{i,j}x^i_j $$$$- 一個等式兩邊的自由索引和虛擬索引個數應該一致 $$
洛倫茲變換的推導
假設最簡單的線性變換, (t,x,y,z)代表s系,另外的一個代表s', 其他情況更復雜的情況都可以從基本情況推出來 $$ \begin{cases} t'=\alpha t + \beta x \\\\ x'=\gamma t + \sigma x \\\\ y'=y\\\\ z'=z\\\\ \end{cases} $$
$$這里的\alpha,\beta,γ和\sigma 都只依賴于v,如果 x=vt,則 x′ = 0$$
因為相對我s系是vt,就說明我是起點,因為是勻速直線運動 代入第二個式子得
$$x' = \sigma (v)?(x?vt ) ①$$
$$相對另一物體速度為0時,說明x=x^′,則此時\sigma =1 ,即\sigma (0)=1$$
$$根據相對性原理,s觀察s'的相對速度是-v,代入 x = \sigma (?v)(x^′+vt^′ ) ②$$
$$由2式可得 : \frac{x?\sigma x^′}{\sigma v}= t' $$
$$將1式代入2式可得 (\frac{1}{\sigma v}?\frac{\sigma }{v})x+\sigma t=t^{'} ③式$$
$$將該式與方程組中第一個方程對比,可得 \sigma =\alpha$$
$$再由四維時空中兩點的間隔對于兩種參照系下相等:$$
$$ t^′2?x^′2= t^2?x^2 $$
代入特殊點 x = vt, x' = 0 有:
$$(\frac{x?\sigma x}{\sigma v})^2+0 =?t^2+x^2$$
$$兩邊同除以t得:\frac{1}{\sigma} =?1+v^2 即\sigma =\frac{1}{\sqrt{1?v^2 }}$$
$$將\sigma 代入③式可得\beta=0$$
于是得到洛倫茲坐標變換公式:
$$ \begin{cases} t'=t- \frac{\frac{v^2}{c^2} x}{\sqrt{\frac{1-v^2}{c^2}}}\\\\ x'=\frac{x-vt}{\sqrt{\frac{1-v^2}{c^2}}}\\\\ y'=y\\\\ z'=z\\\\ \end{cases} $$
對時間乘因子ic,c是具有速度量綱的常數,ict就是具有長度量綱的一個虛數了,將ict第四維度,規定坐標變換時,變換矩陣必須正交,用來保證任意兩點的距離不變,比如洛倫茲變換: $$t^′= \frac{\frac{t? vx}{c^2} }{\sqrt{1?(\frac{v}{c})^2 } }$$
通過洛倫茲變換就可以解釋 鐘慢效應,尺短效應等高速運動物體物理特性發生的差異,這里不再詳細解釋。
洛倫茲變換的矩陣形式 $$如果把x,y,z依次記為x_1, x_2 , x_3 ,記ict為x^4,寫成矩陣形式就是: $$$$ \begin{pmatrix}x_1'\\\\ x_2'\\\\x_3'\\\\x_4' \end{pmatrix}= \begin{pmatrix} \gamma & 0 & 0 & i\beta\gamma \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 & 0 \\\\ -i\beta\gamma & 0 & 0 & \gamma \\\\ \end{pmatrix} \begin{pmatrix}x_1\\\\ x_2\\\\x_3\\\\x_4 \end{pmatrix} $$ $$ 上式中 \beta = \frac{v}{c} , \gamma =\frac{1}{\sqrt{1-(\frac{v}{c})}} $$$$ $$此時 s^2=x_1^2+x_2^2+x_3^2+x_4^2=r^2+(ict)^2 $$ $$注意這里說的x是\Delta x,即物體的距離s^2= r^2?(ct)^2$$ $$s就是四維時空兩點中的間隔, 為了后面統一表述這里將s^2 替換成 ds^2 $$ $$他們并沒有什么差別,d是距離而不是微分, 將ds^2 表示成矩陣相乘的形式 $$ $$ ds^2 = \begin{pmatrix}-1 & & &\\\\ & 1 & & \\\\ & & 1 &\\\\& & & 1 \end{pmatrix} \begin{pmatrix}c^2t^2\\\\ x_2^2\\\\x_3^2\\\\x_4^2 \end{pmatrix}=\eta?(c^2 t^2, x_1^2,x_2^2,x_3^2 ) $$ $$ 其中 \eta_{\alpha\beta}=diag(?1,1,1,1),這里 \eta_{\alpha\beta} 對角線有三正一負,$$ $$這里的系數矩陣稱為\eta,也被稱為閔可夫斯基度量(度規), 那么距離也可以表示成 $$ $$ds^2= \sum_{\mu=0}^3\sum_{\nu=0}^3\eta_{\mu\nu} x^\mu x^\nu$$ $$如果用愛因斯坦取和標記表示 ds^2=\eta_{\mu\nu} x^\mu x^\nu (\mu、\nu為矩陣的行和列的取值)$$ $$在閔可夫斯基空間V中的適合 s^2=0的x稱為類光向量或者零矢量,$$ $$ 或稱x是類光的(lightlike)(因為此時空間距離x^2=(ict)^2 ),$$ $$V中適合 \eta(x,x)>0的向量 x 成為類空向量或稱x是類空的(spacelike ),$$ $$適合\eta(x,x)\lt 0 的向量x稱為類時向量或稱x是類時的(timelike) , $$$$閔可夫斯基空間中所有零矢量的集合構成了該時間所有事件的光錐$$
流形是局部具有歐幾里得空間性質的空間,流形的定義體現了坐標系是局部的,并限制了這些局部范圍內坐標允許的變換, 一個表面是一個二維流形,時空是一個四維流形,經典力學空間和廣義相對論所用時空都是流形,$$黎曼流形具有正定的量度,即 ds^2 始終為正$$

5. 度規張量($g_{\mu\nu}$):
我們命名時空時空坐標$$\xi^\alpha 即 \xi^0=CT,\xi^1=Y, \xi^2=Y,\xi^3=Z $$ 我們繼續表述在新參考系下坐標進行微分: $$d\xi^\alpha =\frac{\partial \xi^\alpha }{\partial x^0 }dx^0+\frac{\partial \xi^\alpha }{\partial x^1 } dx^1+\frac{\partial \xi^\alpha }{\partial x^2 } dx^2+\frac{\partial \xi^\alpha}{\partial x^3} dx^3 $$$$ d\xi^\alpha = \frac{\partial \xi^\alpha}{\partial x^\mu} dx^\mu,d\xi^\beta= \frac{\partial \xi^\beta}{\partial x^ \nu} dx^\nu $$ $$那么 ds^2=\eta_{\alpha \beta} \frac{\partial \xi^\alpha}{\partial x^\mu} \frac{\partial \xi^\beta}{\partial x^ \nu} dx^\nu dx^\mu =g_{\mu\nu} dx^ \nu dx^\mu $$ $$其中 g_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi^\alpha }{\partial x^\mu } \frac{\partial \xi^\beta}{\partial x^\nu } $$ $$ 可以看到g_{\mu\nu}=g_{\nu\mu},因為\eta是一個對角矩陣 $$ $$ 我們將g的逆表示成 g^{\mu\alpha} $$ $$ g^{\mu\alpha} g_{\alpha\nu}=(\eta_{\gamma\beta} \frac{\partial \xi^\gamma}{\partial x^\alpha} \frac{\partial \xi^\beta}{\partial x^\mu })^{-1}? (\eta_{\gamma\beta} \frac{\partial \xi^\gamma}{\partial x^\alpha} \frac{\partial \xi^\beta}{\partial x^\nu }) $$$$=\frac{\partial \xi^\beta}{\partial x^\mu }^{-1}?\frac{\partial \xi^\gamma}{\partial x^\alpha }^{-1}?\eta_{\gamma\beta}^{-1}? \eta_{\gamma\beta}?\frac{\partial \xi^\gamma}{\partial x^\alpha } \frac{\partial \xi^\beta}{\partial x^\nu} = \delta_\nu^\mu (Kronecker delta) $$ $$ 上面這個表示和結果非常重要,后面也要用到 g_{\mu\nu} 非常重要就在于 $$$$ 它包含了所有關于時空和引力場的信息,g_{\mu\nu}一共有16個項$$$$ 但是由于對稱的原因合并下來只有10個項就是上三角或下三角那10個 $$

6. 測地線方程:
對等效原則的考慮,如果我們要描述一個物體在地球引力場中運動,必須遵循以下步驟: $$ 1.用局部慣性自由落體參考系來描述運動 $$ $$ 2.對局部慣性參考系進行變換,變換到大地參考系 $$ $$ 1.用自由落體參考系來描述運動 $$ $$ 在自由下落的參考系中,我們命名時空坐標為\xi^\alpha ,其中\alpha \in {0,1,2,3} $$ $$ \frac{d^2 \xi^\alpha}{d\tau ^2}=0 , ds^2=cd\tau ^2 $$$$ (\because t' = \frac{t ? \frac{v^2}{c^2} x}{\sqrt{\frac{1?v^2}{c^2}}} \therefore dt' = cdt \Rightarrow ds^2=cd\tau ^2) $$ $$ 這里\tau 值得是在靜止參考系中觀察者測量的時間,也稱為固有時間 $$ $$ 2.在大地參考系中描述運動(向上加速) $$ $$ 令x^\mu 是任意非慣性參考系的各軸 $$ $$ 有: \frac{d\xi^\alpha }{d\tau} =\frac{\partial \xi^\alpha }{\partial x^\mu} \frac{dx^\mu}{d\tau} $$ $$ 這就是愛因斯坦取和標記: 對于上式實際上為 \frac{d\xi^\alpha }{d\tau} =\sum_{i=0}^{3}\frac{\partial \xi^\alpha }{\partial x^i} \frac{dx^i}{d\tau} $$ $$ 將鏈式法則運用到自由落體方程中有: $$ $$ 0 = \fracw0obha2h00{d\tau} (\frac{d\xi^\alpha }{d\tau}) =\fracw0obha2h00{d\tau}( \frac{\partial \xi^\alpha }{\partial x^\mu } \frac{dx^\mu}{d\tau}) $$ $$ = \fracw0obha2h00{d\tau} (\frac{\partial \xi^\alpha }{\partial x^\mu }) \frac{dx^\mu}{d\tau} +\frac{\partial \xi^\alpha}{\partial x^\mu } \frac{d^2 x^\mu}{d\tau ^2 } $$ $$ = \fracw0obha2h00{d\tau} (\frac{\partial \xi^\alpha }{\partial x^\mu }) \frac{dx^u}{dx^\nu } \frac{dx^ \nu}{d\tau} +\frac{\partial \xi^\alpha}{\partial x^\mu } \frac{d^2 x^\mu}{d\tau ^2 } $$ $$ = \frac{dx^\nu}{d\tau} (\frac{\partial \xi^\alpha}{\partial x^\mu \partial x^ \nu }) \frac{dx^\mu}{d\tau} +\frac{\partial \xi^\alpha }{\partial x^\mu } \frac{d^2 x^\mu}{d\tau ^2 } $$ $$ 兩邊同時乘\frac{\partial x^\beta}{\partial \xi^\alpha} 得: $$ $$ 0 = \frac{\partial x^\beta}{\partial \xi^\alpha } \frac{dx^\nu}{d\tau} (\frac{\partial \xi^\alpha}{\partial x^\mu \partial x^ \nu }) \frac{dx^\mu}{d\tau} +\frac{\partial \xi^\alpha }{\partial x^\mu} \frac{d^2 x^\mu}{d\tau ^2 } \frac{\partial x^\beta}{\partial \xi^\alpha} $$ $$ 令\frac{\partial x^\alpha }{\partial x^\mu }=\delta_\mu^\beta (Kronecker delta 克羅內科函數, $$$$即如果\beta和\mu一致值為1,不一樣則值為0 ) 帶入可得: $$ $$ 0 = \frac{\partial x^\beta}{\partial \xi^\alpha} \frac{dx^\nu}{d\tau} \frac{\partial \xi^\alpha }{\partial x^\mu \partial x^ \nu } \frac{dx^\mu}{d\tau} +\delta_\mu^\beta \frac{d^2 x^\mu}{d\tau ^2 } 因為只有相等時為1,所以可以用\beta代替\mu ,即 $$$$ 0 = \frac{\partial x^\beta}{\partial \xi^\alpha} \frac{dx^\nu}{d\tau} \frac{\partial \xi^\alpha }{\partial x^\mu \partial x^ \nu } \frac{dx^\mu}{d\tau} +\frac{d^2 x^\beta}{d\tau ^2 } $$ $$ 最終: 0 = \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial\tau} \frac{\partial x^ \nu}{\partial \tau} (測地線方程Geodesic equation) $$ $$ 其中 \Gamma_{\mu \nu}^\beta= \frac{\partial x^\beta}{\partial \xi^\alpha} \frac{\partial \xi^\alpha}{\partial x^\mu \partial x^ \nu } (Christoffel symbol) $$ $$ 上式被稱為測地線方程 $$ $$ 通過方程可知: $$ $$ 1. 在加速的參考系下,粒子的運動不再是直線運動了,因為某種慣性力施加在它上面: $$$$f^\beta=?m \Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial \tau } \frac{\partial x^ \nu}{\partial \tau} $$$$ 上述環境如果實在重力場中進行自由落體,那么慣性力就是重力了, $$$$ 如果我們知道christoffel符號的組成部分,我們就可以確定上述中物體的運動速度了。 $$$$ - 這個等式將直線運動推廣到了彎曲的時空中,等會我們會介紹如按照度量張量 $$$$看到從時空度兩種計算christoffel符號 $$$$ - 該方程實際上代表10項的4個不同方程\beta從0到3, \mu和 \nu 的組合$$$$會有16種,但其中有些對稱 所以只有10個 $$$$- 在同一個測地線方程中,我們將在牛頓極限測地線方程中演示如何在$$$$特定條件下推導張量和重力之間的直接關系。 $$

8.Christoffel張量

9.Christoffel符號2(連接系數)

10. 協變導數:
在微分幾何里,人們希望推廣這個概念到一般微分流形上。首先求導(或求微)的對象從函數推廣到向量場(就是向量叢的截面,如切向量場和余切向量場), 定義域則移到了整個流形上(不再是平坦的空間), 求導的方向可以是任何切向量的方向。 這樣得到的導數就稱為協變導數,其微分稱為協變微分。
向量的協變微分
$$ 對于一個向量V = V^\alpha e_{\alpha} 其對x^{\beta} 求偏導 為:\frac{ \partial V}{\partial x^\beta }=\frac{\partial V^\alpha }{\partial x^\beta} e_\alpha +V^{\alpha} \frac{\partial e_\alpha }{\partial x^\beta } $$$$ 之前我們得到連接系數為: \Gamma_{\alpha \beta}^\gamma (e_\gamma ) = \frac{\partial e_{\alpha} }{\partial x^\beta } $$$$ 將其帶入上式可得: \frac{\partial V}{\partial x^\beta} =\frac{\partial V^\alpha }{\partial x^\beta } e_\alpha +V^\alpha \Gamma_{\alpha \beta}^\gamma e_\gamma $$$$ 等式的右側有兩個虛擬符號\alpha 和\gamma ,交換他們 (為什么能交換) $$$$ \frac{\partial V}{\partial x^\beta}=\frac{\partial V^\alpha }{\partial x^\beta} e_\alpha +V^\gamma \Gamma_{\gamma\beta}^\alpha e_\alpha , 提出e_\alpha $$$$ \frac{\partial V}{\partial x^\beta}=(\frac{\partial V^\alpha }{ \partial x^\beta } +V^\gamma \Gamma_{\gamma\beta}^\alpha )e_\alpha $$$$ 此表達式表示V在x的\beta方向上的變化率 $$$$ 可以用 \nabla來表示 協變導數值: $$$$\nabla_\beta V^\alpha =\frac{\partial V^\alpha }{ \partial x^\beta } +V^\gamma \Gamma_{\gamma\beta}^\alpha $$$$ \nabla_\beta V^\alpha 的等價符號是 D_\beta V^\alpha 和 V_{;\beta}^\alpha $$$$ 備注: $$$$ - 度規張量的偏導數消失在M的任何點等價于Christoffel符號的消失, $$$$這樣我們可以在任何慣性或局部慣性狂阿基背景下重寫整個基本等式: $$$$\nabla_\beta V^\alpha =\frac{\partial V^{\alpha} }{\partial x^\beta } $$$$ - Christoffel符號本身不會轉換成張量是因為,總可以找到令Christoffel為0 $$$$ 的局部慣性系,但對于張量卻不會。 $$$$ 此外還可以推導出協變向量的協變微分。 由于此等式對于每個任意A向量都成立,$$$$因此方括號中的數量必須為null。因此,我們證明了向量B的協變分量的$$$$協變導數的表達式如下: $$$$ \nabla_\alpha B_\mu = \frac{\partial B_\mu}{\partial x^\alpha} - B_\sigma \Gamma^\sigma_{\alpha \mu} $$$$ 其中B為協變向量 $$
11. 黎曼張量
換向差(commutator):表示一個操作整箱和方向的差異如:[AB] = AB-BA ,如果更改順序后沒有影響,則換向差為0 ,因為在平坦的空間求協變微分操作先后都一樣將換向差應用于協變微分的任何非零結果都可以歸因與空間的曲率,從而歸因于黎曼張量, 黎曼張量實際上衡量了時空的曲率
$$ 我們通過計算協變微分的換向差(commutation)\nabla_c \nabla_b V_\alpha ?\nabla_b \nabla_c V_\sigma $$$$來推導黎曼張量 或者用分號表示:V_{\alpha ;bc} ?V_{\alpha ;cb} $$$$ 前面推導的協變微分為:\nabla_b V_\alpha =\partial _b V_\alpha ?\Gamma_{ab}^d V_d $$$$ 于是: \nabla_c \nabla_b V_\alpha = \partial _c (\nabla_b V_\alpha )?\Gamma_{\alpha c}^e \nabla_b V_e ?\Gamma_{bc}^e \nabla_e V_\sigma $$$$ 其中右側第一項:\partial _c (\nabla_b V_\alpha )=\partial _c \partial _b V_\alpha ?\partial _c (\Gamma_{ab}^d V_d ) $$$$ \partial _c (\nabla_b V_\alpha )=\partial _c \partial _b V_\alpha ?\partial _c (\Gamma_{ab}^d ) V_d?\partial _c \Gamma_{ab}^d (V_d ) $$$$ 右二\Gamma_{ac}^e \nabla_b V_e=\Gamma_{ac}^e (\partial _b V_e ?\Gamma_{be}^d V_d) $$$$ 右三\Gamma_{bc}^e \nabla_e V_\alpha =\Gamma_{bc}^e (\partial _e V_\alpha ?\Gamma_{\alpha e}^d V_d ) $$$$ 帶入公式可得\nabla_c \nabla_b V_\alpha = $$$$\partial _c \partial _b V_\alpha - \partial _c (\Gamma_{ab}^d ) V_d ?\partial _c (V_d ) \Gamma_{ab}^d ?\Gamma_{ac}^e (\partial _b V_e?\Gamma_{be}^d V_d )?\Gamma_{bc}^e (\partial _e V_\alpha ?\Gamma_{ae}^d V_d ) $$$$ 然后交換bc可得\nabla_b \nabla_c V_\alpha $$$$ = \partial _b \partial _c V_\alpha - \partial _b (\Gamma_{ac}^d ) V_d ?\partial _c (V_d ) \Gamma_{ac}^d ?\Gamma_{ac}^e (\partial _c V_e?\Gamma_{ce}^d V_d )?\Gamma_{cb}^e (\partial _e V_\alpha ?\Gamma_{ae}^d V_d ) $$$$ 計算\nabla_c \nabla_b V_\alpha ?\nabla_b \nabla_c V_\alpha $$$$ = - \partial _c (\Gamma_{ab}^d ) V_d ?\partial _c (V_d ) \Gamma_{ac}^d ?\Gamma_{ac}^e (\partial _c V_e?\Gamma_{ce}^d V_d )?\Gamma_{cb}^e (\partial _e V_\alpha ?\Gamma_{ae}^d V_d ) $$$$ 展開: \nabla_c \nabla_b V_\alpha ? \nabla_b \nabla_c V_\alpha $$$$ = ?\alpha _c (\Gamma_{ab}^d ) V_d ?\alpha _c (V_d ) \Gamma_{ab}^d ? \Gamma_{ac}^e \partial _b V_e+\Gamma_{ac}^e \Gamma_{be}^d V_d+\partial _b (r_ac^d ) V_d+\partial _b (V_d ) \Gamma_{ac}^d+\Gamma_{ab}^e \partial _c V_e+\Gamma_{ce}^d V_d $$$$ = \partial _b (V_d ) \Gamma_{ac}^d ?\partial _c (V_d ) \Gamma_{ab}^d+\Gamma_{ab}^e \partial _c V_e ?\Gamma_{ac}^e \partial _b V_e+(\partial _b (\Gamma_{ab}^d )?\partial _c (\Gamma_{ab}^d )+\Gamma_{ac}^e \Gamma_{be}^d ?\Gamma_{ab}^e \Gamma_{ce}^d ) V_d $$$$ 前面我們計算出Christoffel的另一種表示\Gamma_{\alpha \beta}^\Gamma e_\gamma = \frac{\partial (e_{\alpha } )}{\partial x^\beta } $$$$ 因此: \Gamma_{ab}^e \partial _c V_e ? \Gamma_{ac}^e \partial _b V_e= \partial _c \Gamma_{ab}^e V_e ?\partial _b \Gamma_{ac}^e V_e (偏導順序無關)$$$$ =\partial _c \partial _b V_a?\partial _b \partial _c V_\alpha =0 $$$$ 通過交換b,c 可以得到: \partial _b (V_d ) \Gamma_{ac}^d ?\partial _c (V_d ) \Gamma_{ab}^d=0 $$$$ 最后,commutation為: $$$$ \nabla_c \nabla_b V_\alpha ? \nabla_b \nabla_c V_\alpha =(\partial _b (\Gamma_{ac}^d ) ?\partial _c (\Gamma_{ab}^d )+\Gamma_{ac}^e \Gamma_{be}^b ?\Gamma_{ab}^e \Gamma_{ce}^d ) V_d=R_{abc}^d V_d $$$$ 將R_{abc}^d 稱為黎曼張量。 $$$$ 簡化表示成:R_{abc}^d= \Gamma_{ac,b}^d ?\Gamma_{ab,c}^d+\Gamma_{ac}^e \Gamma_{be}^d ?\Gamma_{ab}^e \Gamma_{ce}^d $$$$ 因為有4個索引,所以 每個索引有4種取值,所以一種有4^4=256個項 $$

12.張量收縮
坐標系變換
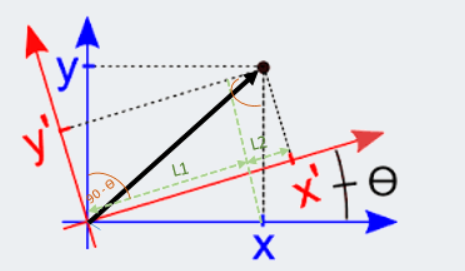
$$對坐標系旋轉\theta 可以得到新的坐標系,則向量A在兩個坐標系下的坐標分別為: $$$$ A=A^x e_x+A^y e_y $$$$ A=A^′x e_x+a^′y e_y $$$$ 其中A^{′x}=L_1+L_2 $$$$ L_1=A^x cos?(\theta ) $$$$ L_2=A^y cos?(\pi/2?\theta ) $$$$ 則(A^′)^x= A^x cos?(\theta )+A^y cos?(\pi/2?\theta ) $$$$ 同理 A^′y= A^x cos?(\pi/2+\theta )+A^y cos?(\theta ) $$$$ 則A'就可以表示成矩陣的乘法: $$$$ \begin{pmatrix} A^{'}_{x} \\\\ A^{'}_{y} \end{pmatrix} = \begin{pmatrix} cos(\theta) & sin(\theta) \\\\ -sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix}A^{x}\\\\ A^{y} \end{pmatrix} $$
基向量變換
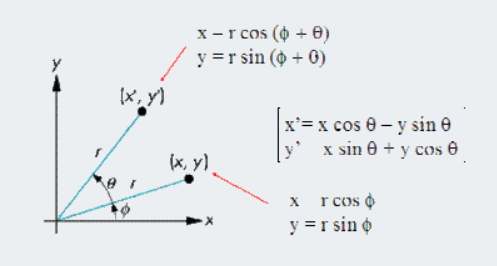
$$在新的基向量上表示旋轉后的向量,對于向量逆時針旋轉\theta 相當于順時針將坐標系旋轉\theta $$ $$ \begin{pmatrix} A^{'}_{x} \\\\ A^{'}_{y} \end{pmatrix} = \begin{pmatrix} cos(\theta) & -sin(\theta) \\\\ sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix}A^{x}\\\\ A^{y} \end{pmatrix} $$$$ dx^{′1}=(\partial x^{′1})/(\partial x^{1} ) dx^1+(\partial x^{′1})/(\partial x^2 ) dx^2 $$$$ dx^{′2}=(\partial x^{′2})/(\partial x^1 ) dx^1+(\partial x^{′2})/(\partial x^2 ) dx^2 $$$$ dx^{'i}=\frac{\partial x^{'i}}{\partial x^j} dx^j $$$$ 計算適當的導數我們得到: $$$$ \frac{\partial x^{'1}}{\partial x^1} = cos\theta \qquad \frac{\partial x^{'2}}{\partial x^1} = sin \theta $$$$ \frac{\partial x^{'1}}{\partial x^2} = -rsin\theta \qquad \frac{\partial x^{'2}}{\partial x^2} = rcos\theta $$$$ 因為dx^{'1}和d^{'2}實際上反映了e_1 和e_2 的大小所以: $$$$ e_1 = \frac{\partial x^{'1}}{\partial x^1} \vec{i} +\frac{\partial x^{'2}}{\partial x^1} \vec{j} = cos \theta \vec{i}+\ sin\theta vec{j} e_2 = \frac{\partial x^{'1}}{\partial x^2} \vec{i} +\frac{\partial x^{'2}}{\partial x^2} \vec{j} = -rsin\theta \vec{i} + rcos\theta \vec{j} $$$$這樣我們就得到了分量A^{'i}的定義,又稱為逆變(反變或contravariant)分量 $$$$ A^{'i} = \frac{\partial x^{'i}}{\partial x^j} A^j $$
協變分量和逆變分量
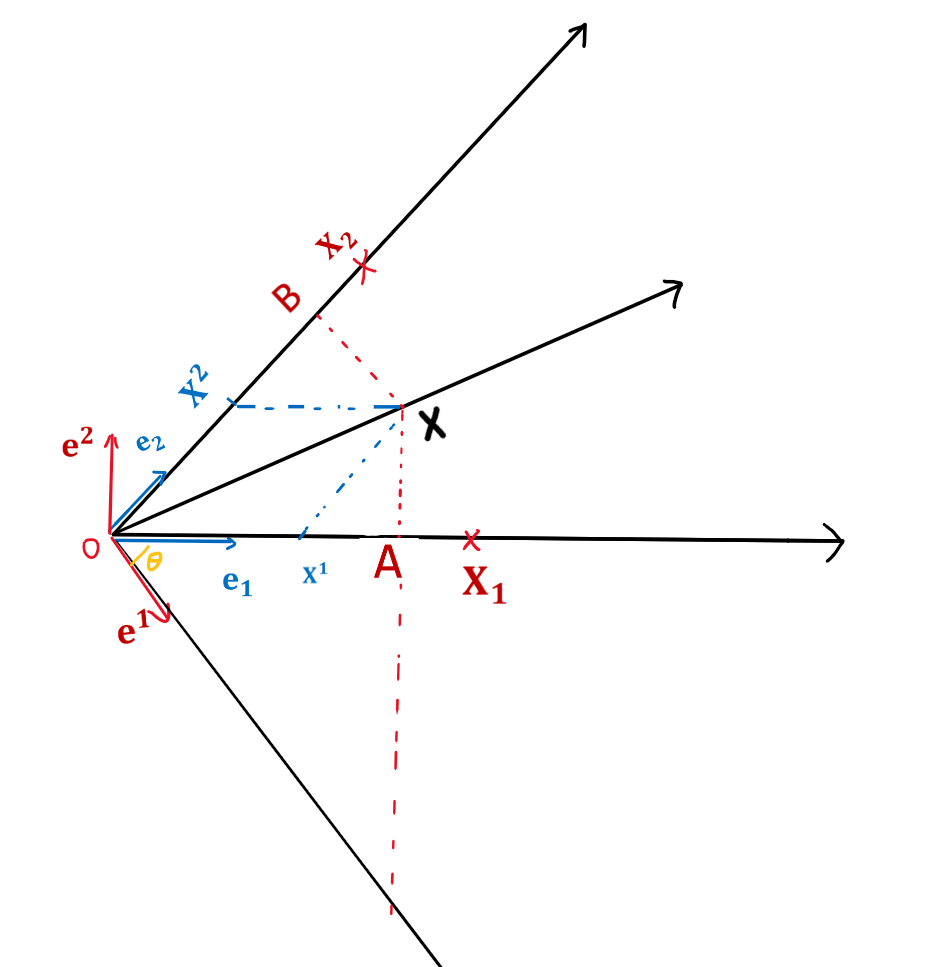
$$ 圖中 X = e_1 x^1+e_2 x^2 $$$$ 我們構造了e_1 和 e_2 的對偶向量e^1 和 e^2,我們希望用對偶向量表示原向量X $$$$ 我們令 協變分量為 x_1= e_1 x ,注意協變分量是標量 $$$$ 我們期望的結果是: X = e^1 X_1+e^2 X_2 $$$$ 對偶向量是對于e^i滿足\lt e^i,e_j \gt =\delta_j^i 的向量e^j $$$$ 舉個例子:e^1 是 e_1 的對偶向量,他滿足 e^1 \cdot e_1=1 $$$$ 即對偶空間的相同下標的基向量內積為1, 關于對偶空間和對偶基可以看: $$ https://blog.csdn.net/sumx2015/article/details/78909635 解釋的很形象了 $$ 對偶基的要求還蘊含了任意非相同標記的基向量和對偶基向量內積為0,就是說他們垂直 $$$$ 下面我們來證明為什么這樣的向量可以構造出來新的基底 $$$$ 由圖根據平行四邊形法則我們可知: $$$$ |x|sin\theta =|e^1 x_1 |cos\theta $$$$ sin\theta =\frac{|e^1 (e_1 x)|}{|x|} cos\theta $$$$ sin\theta =\frac{|e^1 | e_1 |cos?(\pi/2?\theta ) |}{|x|} cos\theta $$$$ 1 = |e^1| |e_1|cos\theta $$$$ 即e^1 e_1=1 , 同理可以證明e^2 e_2=1 $$$$ 反過來 也可以推導出 |x|sin\theta =|e^1 x_1 |cos\theta $$$$ 所以\lt e^i,e_j\gt =\delta_{j}^{i} 是滿足協變分量為x_1= \lt e_1 ,x\gt 的原向量X在對偶空間上的表示 $$$$ 尤其是當 e_1=1時,A點就和 X_1 重合了,此時X_1 就是x在 e_1 軸上的投影 $$$$ 對于逆變分量, 如果改變基向量e_1 的大小,為了保證X= e則逆變分量X^1 的大小會反向改變, $$ 比如基向量減小 一半,逆變分量就會增加一倍, 而對于協變分量,如果原空間的基向量模增加一倍, 對偶空間的基向量模減小一倍,因為內積為1的約束, 對應協變分量就增加一倍,所以 協變指的是,隨著原空間的基向量的變化而正相關變化 之前我們推導對于逆變張量的分量: $$ A^{'i} = \frac{\partial x^{'i}}{\partial x^{'i}} A^j $$$$ 同理對協變張量的分量效果也是一致的: $$$$ A_{'i} = \frac{\partial x^{'i}}{\partial x^{'i}} A_j $$
張量的縮放
當把上面的逆變張量和協變張量推廣到普通情況就相當復雜: $$ 令原張量表示成: S_{j_1 j_2?j_q}^{i_1 i_2?i_p } $$$$ 則經過變換后的矩陣\bar{S}可以表示成: $$$$ \bar{S}_{j_1 j_2?j_q}^{i_1 i_2?i_p}= S_{\beta_1 \beta_2?\beta_q}^{\alpha_1 \alpha_2?\alpha_p}\frac{\partial \bar{x}^{i_1 }}{\partial x^{\alpha_1}} \frac{\partial \bar{x}^{i_2 }}{\partial x^{\alpha_2}}\cdots \frac{\partial \bar{x} ^{i_p }}{\partial x^{\alpha_p } } \frac{\partial \bar{x} ^ {\beta_1}}{\partial x^{j_1}} \frac{\partial \bar{x} ^{\beta_2}}{\partial x^{j_2 }}\cdots \frac{\partial \bar{x} ^{\beta_p }}{\partial x^{j_q }} $$$$ 當我們嘗試讓某個上標i_k 和某個下標j_b 相等時,就可以在右式中約去, $$$$ 反映到左式中就可以直接約去,我們把這種操作叫做contraction $$$$ 張量壓縮,當然我們也可以進行擴張,制造兩個相同的下標。 $$$$ 度量張量最有用的功能之一就是在其他張量的協變量和范變量分量之間進行轉換 $$$$ 因為對 度規張量進行變換可以得到: $$$$ g_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi ^{\alpha}}{\partial x^\nu} \frac{\partial \xi ^\beta}{\partial x^\nu} $$$$ g^{'}_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi ^{\alpha}}{\partial x^{'\nu}} \frac{\partial \xi ^\beta}{\partial x^{'\nu}} = \eta_{\alpha \beta} \frac{\partial \xi ^ \alpha}{\partial x^\sigma}\frac{\partial x^\sigma}{\partial x^{'\mu}} \frac{\partial \xi^\beta}{\partial x^\rho} \frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ g^{'}_{\mu\nu} =\eta_{\alpha \beta} \frac{\partial \xi ^ \alpha}{\partial x^\sigma} \frac{\partial \xi^\beta}{\partial x^\rho} \frac{\partial x^\sigma}{\partial x^{'\mu}} \frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ g^{'}_{\mu\nu} = g_{\sigma \rho}\frac{\partial x^\sigma}{\partial x^{'\mu} }\frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ 之所以能夠進行壓縮,是因為度規張量恰好 $$$$ 需要對下標求偏導,如上面的壓縮一樣,對相同的標記進行了約分。 $$$$ 因此,給定張量的逆變分量和原始基向量,并希望確定協變分量, $$$$一種方法可能是確定對偶基向量, 如g_{ij} A^j=A_i ,g^{ij} A_i=A^j , g^{ij} A_i=A^j $$

13.Ricci張量和Ricci標量

14. 能動張量:
$$ 應力能量動量張量(Stress \quad energy \quad momentum \quad tensor,SEM):T^\alpha \beta $$$$ 簡稱能動張量,用來描述能量和動量在時空中的密度與通量(flux), $$$$其為牛頓物理中應力張量的推廣,能動張量在廣義相對論中是重力場的源, T^\alpha $$$$ \beta 給出四維動量或4-動量P(\frac{E}{c},p_x,p_y,p_z)之\alpha 分量$$$$(\alpha ,\beta依次代表1,2、、)通過一個坐標為常數x^b 表面的通量, $$$$ 另外要注意的是SEM 是對稱的(當自旋張量為0時), 即T^{ab}=T^{ba} $$$$ T^{00} 代表能量密度 , T^{0i} 代表能量通過x^i 表面的能量密度,$$$$等同于 T^{i0} 第i動量之動量密度,當\alpha \beta $$$$ 不同時表示剪應力,相同時表示正向應力。 $$$$ 由于我們最終的目標是在時空幾何圖形及其內容之間建立關系,$$$$因此我們首先必須找到用什么來描述,$$$$由于質量,能量和動量都相關(E^2=p^2 c^2+m_0^2 c^4), $$$$ 證明:p^2=(m_0 c)^2 , $$$$ p^2= \eta_u \nu p^\mu p^ \nu=\frac{E^2}{c^2} $$$$ ?p_x^2?p_y^2?p_z^2=\frac{E^2}{c^2} ?p^2?(m_0 c)^2=\frac{E^2}{c^2 ?p^2}\Rightarrow E^2 = p^(2c^2 ) $$$$ 所以似乎假設: 廣義相對論的引力場來源應該包括動量,能量和質量。 $$$$另一方面,用泊松方程( 泊松方程:\nabla^2 \phi=f ,就是各維的二階偏導數之和, ) $$$$ 表示的描述由質量密度引起的重力的等效牛頓方程為: $$$$? \nabla g=?\nabla(?\nabla\phi)=4\pi G\rho $$$$ 那么能量密度是張量還是標量呢? $$$$ 先考慮相對靜止的非相互作用例子相對于彼此的提及dxdydz,,也被稱作 dust cloud $$$$ 在它自己的參考系,這個dust有自己的能量密度(質量密度) \rho _0=m_0 n_0 , $$$$在這里m_0 代表了塵粒的質量, n_0 $$$$ 代表了單位提及例子的數量,在洛倫茲變換下,會變成: $$$$ m_0 \Rightarrow m_0 \Gamma , n_0→n_0 \Gamma\Rightarrow \rho _0 \Rightarrow\rho =\rho _0 \Gamma^2 u^\mu=\Gamma(1,v) $$$$ =(\Gamma,v_x \Gamma, v_y \Gamma,v_z \Gamma)^T=(u^t,v_x u^t, v_y u^t,v_z u^t )^T $$$$ 所以設置\Gamma= u^t 使用這種相等性,并且每個粒子的能量等于p^t=mu^t,$$$$ 我們改寫S'中的總能量密度: $$$$ \rho ≡np^t=(n_0 u^t )(mu^t )=(n_0 m) u^t u^t=\rho _0 u^t u^t $$$$ 可以將\rho 解釋成對稱的二維張量,也就是我們說的能動張量, T^{\mu \nu}=T^ \nu\mu=\rho _0 u^\mu u^ \nu $$$$ 上述可知T^{00} 可表示成能量密度 ,對于4x4的其他項來說: $$$$ T^tx=\rho _0 u^t u^x=(n_0 m) u^t u^x=(n_0 u^t )(mu^t ) v_x=np^t v_x=\frac{(nAv_x dt) p^t}{Adt} $$$$ 其中A_vx dt 代表了 在dt時間內垂直x方向穿過表面A的dust體積, $$$$ 可以表示通過該表面的顆粒總數, $$$$ 則T^tx=T^xt 除了T的第一行和第一列外,其他的部分我們表示成 $$$$ T^kl=\rho_0 u^k u^l=(n_0 m) u^k u^l=(n_0 m) u^t v_k u^l=(n_0 u^t ) v_k (mu^l )= $$$$nv_k (mu^l )=nv_k p^l=mv_k p^l=\frac{(nAv_k dt) p^l}{Adt} $$$$ 其中p^l 是動量,則T^{kl} 表示l動量在k方向的通量, $$

15.牛頓極限
牛頓極限: 是一種數學近似值,用于表示(1)弱引力(2)與光速相比運動緩慢的物體(3)緩慢改變引力場的物理系統,在這種情況下,牛頓萬有引力定律可以用于獲得準確的值, 在牛頓極限中,時空近似平坦,并且可以在有限距離內使用閔可夫斯基度量,

16.測地線方程2和 度規張量分量g的00分量.:
$$ 牛頓引力由兩個方程組成:一個高速我們我們物質如何對引力做出反應,$$$$另一個告訴我們物質如何產生引力。 $$$$ 第一個方程是從牛頓第二定律中得到:$$$$ a = -\nabla\phi 表示加速度為a, \phi為力 (加速度為力的負梯度??) $$$$ 測地線方程描述的是僅受中立作用的粒子的世界線,因此我們的目標是證明,$$$$ 在牛頓極限的情況下,測地線方程可簡化成第一個牛頓重力方程 $$$$ 測地線方程為:$$$$ 0 = \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial \tau} \frac{\partial x^ \nu}{\partial \tau} $$$$ 因為粒子運動緩慢所以時間分量支配了其他分量, $$$$ 因此我們可以近似的得出: 由于: \frac{dx^i}{d\tau } \ll \frac{dt}{d\tau} $$$$ 0 = \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial \tau} \frac{\partial x^ \nu}{\partial \tau} $$$$≈ \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{00}^\beta (\frac{cdt}{d\tau} )^2 \frac{d^2 x^i}{d\tau ^2 }+\Gamma_{00}^i (\frac{cdt}{d\tau })^2= 0 公式1 $$$$ 前面提到Christoffel符號: \Gamma_{00}^i=\frac{1}{2} g^{ij} (g_{j0,0}+g_{j0,0}?g_{00,j} ) $$$$ 但是因為引力場很弱所以,所以時間導數g_{j0,0} 為0,$$$$ 因此,可以將christoffel 符號簡化成 \Gamma_{00}^i=\frac{1}{2} g^{ij} g_{00,j} $$$$ 如果引力場足夠弱,時空僅略微從狹義相對論的閔可夫斯基空間變形,$$$$ 我們可以考慮時空度量為一個小的擾動閔可夫斯基規度\eta_{\mu \nu} $$$$ 則g_{\mu \nu}=\eta_{\mu \nu}+h_{\mu \nu} , |{\mu \nu}|\ll 1 $$$$ g_{00,j}={(\eta_{00}+h_{00} )}_{,j} g_{00,j}= {\eta_{00}}_{,j} +h_{00,j}=0+h_{00,j} $$$$ 由于\eta_{00}=1 g_{00,j}=h_{00,j} $$$$ 在此步驟中,公式1變成: \frac{d^2 x^i}{d\tau ^2 }=? \Gamma_{00}^i \frac{cdt}{d\tau }^2 $$$$ \frac{d^2 x^i}{d\tau ^2 }= \frac{1}{2} g^{ij} h_{00,j} (\frac{cdt}{d\tau} )^2 $$$$ 如果我們定義 g^{ij}=\eta^{ij} ?h^{ij}, 我們發現g^\mu\sigma g_{\sigma v}=\delta_ \nu^\mu, $$$$ 于是我們得到: $$$$ \frac{d^2 x^i}{d\tau ^2 }= \frac{1}{2} \eta^{ij} h_{00,j} (\frac{cdt}{d\tau} )^2 (\eta來度量g) $$$$ \eta^{ii}=?1, 其他值為0,所以: $$$$ \frac{d^2 x^i}{d\tau ^2 }= ?\frac{1}{2} h_{00,i} (\frac{cdt}{d\tau} )^2 $$$$ 將左側的導數從\tau 改成t,為此,首先將上式中的i替換成0: $$$$\frac{c^2 d^2 t}{d\tau ^2 }=?\frac{1}{2} h_{00},0 \frac{cdt}{d\tau}^2 $$$$ c^2 \frac{d^2 t}{d\tau ^2 }=0 (因為重力場是常數 h_{00},0=0) $$$$ \frac{d^2 t}{d\tau ^2 }=0, $$$$ 有了這個結果,我們仍然需要對\tau 使用偏導數 $$$$ \frac{d^2 x^i}{d\tau ^2 }=\fracw0obha2h00{d\tau} \frac{dx^i}{d\tau} =\fracw0obha2h00{d\tau} (\frac{dt}{d\tau} \frac{dx^i}{dt}) = $$$$ \fracw0obha2h00{d\tau} (\fracw0obha2h00{d\tau} \frac{dx^i}{d\tau} )+\frac{dx^i}{dt} (\fracw0obha2h00{d\tau} \frac{dx^i}{dt})=\frac{dt}{d\tau } (\frac{dt}{d\tau} \fracw0obha2h00{d\tau } \frac{dx^i}{d\tau})+\frac{dx^i}{dt} (\fracw0obha2h00{d\tau} \frac{dt}{d\tau} ) $$$$=(\frac{dt}{d\tau} )^2 (\frac{d^2 x^i}{dt^2} )+\frac{dx^i}{dt} (\frac{d^2 t}{d\tau ^2 }) $$$$ 所以 \frac{d^2 x^i}{d\tau ^2 }=(\frac{dt}{d\tau} )^2 (\frac{d^2 x^i}{dt^2} ) (制造出對t的偏導數) $$$$ 因為(\frac{d^2 t}{d\tau ^2} ) =0 $$$$ 那么 \frac{d^2 x^i}{d\tau ^2 }=(\frac{dt}{d\tau} )^2 (\frac{d^2 x^i}{dt^2} )=?\frac{1}{2} h_{00,i} (\frac{cdt}{d\tau} )^2 $$$$ \frac{d^2 x^i}{dt^2}=?\frac{c^2}{2} h(00,i) $$$$ 牛頓力學為\frac{d^2 x^i}{dt^2} =?\partial \frac{\phi}{\partial x^i} (\phi為牛頓引力勢 ,可以把這個公式看成已知) $$$$ 最后,以向量形式表示: \frac{d^2 r}{dt^2} =?grad\phi 其中\phi=\frac{c^2 h_{00}}{2} $$$$ 備注: 將度規標準分量g_{00} 表示為: g_{00} =\eta_{00}+h_{00}=1+\frac{2\phi}{c^2} (就是將用\phi表示h_{00}) $$$$ 我們可以看到左側的公制張量 與右側的重力勢之間存在直接聯系 $$$$ 我們可計算地球上的h_{00} 可以得到其為10^(?9) 這意味著因重力場 $$$$而對于minkowski度量的偏差可以忽略不計。 $$

17.愛因斯坦的猜想與驗證:
$$ 愛因斯坦張量微分形式比較,于是推測出 G_{\mu \nu}= \kappa T_{\mu \nu} $$$$ 愛因斯坦想要構造一個等式,左邊是時空的彎曲情況,右邊是時空中的能量。 $$$$ 可以看到已經有了T_{\mu \nu} 現在需要左邊描述時空彎曲的程度, $$$$于是 G_{\mu \nu} 需要 滿足 是一個二維張量就像T_{\mu \nu} 一樣, $$$$ 應該描述使用曲率,并且相對黎曼張量是線性的,具有零散度,最后再牛頓極限下,$$$$應該減小到4\pi G\rho $$$$ 愛因斯坦的第一次嘗試使用了Ricci張量作為解決方案: $$$$ 由 在牛頓極限下的測地線方程:\frac{d^2 r}{dt^2 }=?grad\phi 其中\phi=\frac{c^2 h_{00}}{2} $$$$ 可得到 將公制張量的分量 g_{00} 可以表示成 g_{00}= \eta_{00}+h_{00} =1+\frac{2\phi}{c^2} $$$$ 前面說到g_{\mu \nu} 非常重要就在于 它包含了所有關于時空和引力場的信息 , $$$$ 所以方程中應該也是類似g_{uv} 這種二階導數的形式, $$$$ 愛因斯坦先考慮的是使用黎曼張量的收縮形式:Ricci張量: $$$$ 前面得到的黎曼張量的表達式為: $$$$ R_{abc}^d= \Gamma_{ac,b}^d ?\Gamma_{ab,c}^d+\Gamma_{ac}^e \Gamma_{be}^d ?\Gamma_{ab}^e \Gamma_{ce}^d $$$$ 在靜態和弱引力場的情況下,只有 R_{00} 有貢獻: $$$$ R_{00}=R_{00}a^\alpha =\Gamma_{0\alpha ,0}^\alpha ?\Gamma_{00,a}^\alpha +O(h2 ) = ?\Gamma_{00,i}^i $$$$ 前面提到牛頓極限下,$$$$ \Gamma_{00}^i=\frac{1}{2} g^{ij} (g_{j0,0}+g_{j0,0}?g_{00,j} ) (\eta^{ii}=?1 ? 其他值為0,所以:) $$$$ \Gamma_{00}^i=?\frac{1}{2} g^{ij} g_(00,j) , 因為g^{ij} 受\eta^{ij} 支配,并且 g_{00,j}=h_{00,j} $$$$ 所以\Gamma_{00}^i=?\frac{1}{2} \eta ^{ij} h_{00,j}=\frac{1}{2} \sigma _j^i h_{00,j} $$$$ \Gamma_{00,i}^i=\frac{1}{2} \sigma _j^i h_{00,ij} $$$$ R_{00}= ?\Gamma_(00,i)^i =?\frac{1}{2} (\partial _1^2 h_{00}+\partial _2^2 h_{00}+\partial _3^2 h_{00} ) (00分量占主導) $$$$ =?\frac{1}{2} \nabla^2 h_{00}=?\frac{1}{c^2} \nabla^2 \phi $$$$ 愛因斯坦試圖將R_{ab} 放在愛因斯坦方程的左側,使他等于kT, $$$$ 他甚至用此解決了水星進動的問題,但是因為實際兩邊不等,所以最終愛因斯坦不得不放棄 $$$$ 愛因斯坦的第二次嘗試: $$$$令等式左邊為 G^{\mu \nu}=R^{\mu \nu} ?\frac{1}{2} Rg^{\mu \nu} , $$$$其中 R 是ricci標量,這種形式的G_{ab} 是對稱的,顯然描述了時空曲率, $$$$因此只需證明總導數為0就像右側的能動張量的導數為0 $$$$(表明能量守恒),為此,我們從bianchi \quad identity 開始: $$$$ \nabla_\sigma R_{\alpha \beta}{\mu \nu}+\nabla_ \nu R_{\alpha \beta \sigma \mu}+\nabla_\mu R_{\alpha \beta \nu\sigma} =0 $$$$ 每項都乘上 g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} (因為 g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} 的導數為0 ,所以可以把它們作為常數放到\nabla中) $$$$ \nabla_\sigma g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta}{\mu \nu}+\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta \sigma \mu}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta \nu\sigma} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R+\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta\sigma \mu}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu } g^{\beta \nu} R_{\alpha \beta \nu\sigma} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R+\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu }R_{\sigma \mu\alpha \beta}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_ {\nu\sigma \alpha \beta}=0 $$$$ \nabla_\sigma g^{\gamma\sigma} R?\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\mu\sigma \alpha \beta}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_ {\nu\sigma \alpha \beta}=0 $$$$ Ricci 張量可以表示成 R^{\mu \nu} =g^{\mu\beta} g^{v\sigma} r_{\beta\sigma } 上式改寫為: $$$$ \nabla_\sigma g^{\gamma\sigma} R?\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu } R_{\mu\sigma \alpha \beta}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\nu\sigma \alpha \beta}=0 $$$$ \nabla_\sigma g^{\gamma\sigma} R?\nabla_ \nu g^{\gamma\sigma} g^{\beta \nu} g^{\beta \nu} R_{\sigma \beta } +\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} R_{\sigma \alpha} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R ?\nabla_ \nu R^{\gamma \nu}?\nabla_\mu R^{\gamma\mu}=0 $$$$ \nabla_\sigma g^{\gamma\sigma} R ?\nabla_\sigma R^{\gamma\sigma} ?\nabla_\mu R^{\gamma\sigma} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R ?2\nabla_\sigma R^{\gamma\sigma} =0 $$$$ \nabla_\sigma (g^{\gamma\sigma} R ?2R^{\gamma\sigma} )=0 $$$$ \nabla_\sigma (\frac{g^{\gamma\sigma} R}{2} ?R^{\gamma\sigma} )=0 $$$$ 我們證明了愛因斯坦張量的散度為0 ,所以我們已經找到了愛因斯坦方程的左邊部分 $$

18.常量K:
$$ 前面我們已經得到了愛因斯坦方程是G^{\mu \nu}=kT^{\mu \nu},需要確定常數k $$$$ 謂詞需要證明對于靜態和弱重力場下(牛頓極限)下,愛因斯坦方程可以簡化成牛頓重力定律。 $$$$ 首先使用不同形式的愛因斯坦方程,在計算時能夠更加容易一些。 $$$$ R^{\mu \nu}?\frac{1}{2} g^{\mu \nu} R=kT^{\mu \nu} $$$$ 兩邊同時乘g_{\mu \nu} 可以得到: $$$$ g_{\mu \nu} R^{\mu \nu} ?\frac{1}{2} g_{\mu \nu} g^{\mu \nu} R=kg_{\mu \nu} T^{\mu \nu} $$$$ g_{\mu \nu} R^{\mu \nu}=R 并且 g_{\mu \nu} T^{\mu \nu}=T 所以: $$$$ R?\frac{1}{2} Rg_{\mu \nu} g^{\mu \nu}=kT $$$$ 因為g^{\mu \nu} 是g_{\mu \nu} 的逆 ,他們的乘積是I,因為使用contraction $$$$所以 g_{\mu \nu} g^{\mu \nu}=\delta_ \nu^ \nu =1+1+1+1=4 $$$$ 因此 R ?\frac{1}{2} R× 4=kT $$$$ R = -kT , 將它代入到原式中 $$$$ R^{\mu \nu} ?\frac{1}{2} g^{\mu \nu}× (?kT )= kT^{\mu \nu} $$$$ R^{\mu \nu}+\frac{1}{2} kg^{\mu \nu} T= kT^{\mu \nu} $$$$ R^{\mu \nu}=k(T^{\mu \nu} ?\frac{1}{2} g^{\mu \nu} T) $$$$ 前面我們證明了分量R_{00}≈?\frac{1}{c^2} \nabla^2 \phi $$$$ 但是我們可以指出,當度量從固定時空減少到度量\eta時 ,我們可以通過Ricci張量的定義得到 $$$$ R^{00}=g^0\mu g^0 \nu R_{\mu \nu}≈\eta^0\mu \eta^0 \nu R_{\mu \nu} =(?1)(?1) R_{00} =R_{00} $$$$ R^{00}≈?\frac{1}{c^2} \nabla^2 \phi $$$$ 牛頓限制也意味著 T^{00}=\rho c^2 (因為T = \rho u^u u^ \nu 并且 u^i \ll u^0=c) $$$$ T = g_{\mu \nu} T^{\mu \nu}≈g_{00} T^{00}≈\eta_{00} T^{00}=T^{00} =\rho c^2 $$$$ K再代入R^{\mu \nu}=k(T^{\mu \nu} \frac{1}{2} g^{\mu \nu} T) $$$$ R^{00}=k(T^{00} ?\frac{1}{2} \eta^{00} T) $$$$ ?\frac{4\pi G\rho }{c^2} =K(\rho c^2 ?\frac{1}{2}×1×\rho c^2 ) $$$$ ?\frac{4\pi G\rho }{c^2} =\frac{1}{2} K\rho c^2 $$$$ K = -\frac{8\pi G}{c^4} $$$$ 終于我們得到了完整的愛因斯坦方程R_{\mu \nu} ?\frac{1}{2} g_{\mu \nu} R=?8\pi GT_{\mu \nu} $$
當完全寫出時,EFE(愛因斯坦場方程)由10個耦合的非線性二階偏微分方程組成, 本來是16個,前面講到對于對稱的進行了合并,實際上解愛因斯坦方程就是在解度規張量g,所以相應的方程數為未知數的個數.文章末尾會有github上一個repo提供了對解的驗證,對于正確的解會提供對應的方程中特殊部分的值如黎曼張量等
本文提及的場方程僅僅是最基礎版本的,后來愛因斯坦又在方程中加入了一項宇宙常數,因為他認為宇宙是靜態的,而原始方程解出來是確實膨脹的,所以加了一項常數抵消,但是哈勃證明了他的錯誤,但宇宙常數最后還是被留下來,用來表示宇宙中存在的暗物質和暗能量
參考文章
愛因斯坦場方程推導過程的邏輯梳理:
https://wenku.baidu.com/view/5c305d42ce84b9d528ea81c758f5f61fb7362863.html
本文主要來源,強推,有非常完整的描述:
Einsteinrelativelyeasy http://einsteinrelativelyeasy.com/index.php
另一些類似的網站:
還有對伽利略和麥克斯韋的成果介紹:
http://www.einstein-online.info/spotlights/gr.html
http://newt.phys.unsw.edu.au/einsteinlight/
對偶空間和對偶基的理解:
https://blog.csdn.net/sumx2015/article/details/78909635
維基百科
百度百科
參考視頻:
場方程推導:
協變與逆變向量:
張量的基本運算(包括收縮):
代碼:
spacetimeengine:
github上一個repo提供了對解的驗證,對于正確的解會提供對應的方程中特殊部分的值如黎曼張量等 solution_array = [ metric, coordinate_set, index_config, cosmological_constant ] 僅需要輸入解數組,其中包括了度規和,坐標表示,上下標配置,和宇宙常數即可進行驗證
posted on 2019-11-09 22:32 CaptainHook 閱讀(3161) 評論(0) 收藏 舉報


 浙公網安備 33010602011771號
浙公網安備 33010602011771號