如何用Haskell寫一顆紅黑樹

同步更新于Candy?的新家

Candy?在上學期的數算課上學了紅黑樹，但是他一直沒寫過。

最近他入門了一下Haskell，得知用Haskell可以很方便實現各種樹結構，于是就去學了一下如何用Haskell寫紅黑樹，發現只要不到60行（包括空行和類型簽名）！

下面是一個簡單的小教程。

定義類型

和普通二叉樹一樣噠，只不過加上了一個顏色信息

data Tree a = Nil | Node Color (Tree a) a (Tree a) deriving (Show, Eq)
data Color = R | B deriving (Show, Eq)

輔助函數

• 將樹根染黑：

makeBlack :: Tree a -> Tree a
makeBlack Nil = Nil
makeBlack (Node _ l x r) = Node B l x r

• 將樹根染紅：

makeRed :: Tree a -> Tree a
makeRed Nil = Nil
makeRed (Node _ l x r) = Node R l x r

插入操作

一般的紅黑樹插入不太方便用純函數式來寫，Okasaki在1999年提出了一種新的插入方法，將插入統一為：

• 首先默認插入紅色節點，然后從下向上進行balance操作；
• balance操作會處理當前子樹的children和grandchildren出現雙紅的情況，并且會將當前子樹的根變紅（balance操作并不會改變rank）

插入操作的框架很簡單，需要注意的是最后要讓整棵樹的根變黑：

insert :: (Ord a) => a -> Tree a -> Tree a
insert x = makeBlack . ins 
  where ins Nil = Node R Nil x Nil
        ins t@(Node c l y r) | x < y     = balance $ Node c (ins l) y r
                             | x > y     = balance $ Node c l y (ins r)
                             | otherwise = t

balance操作要處理四種情況：

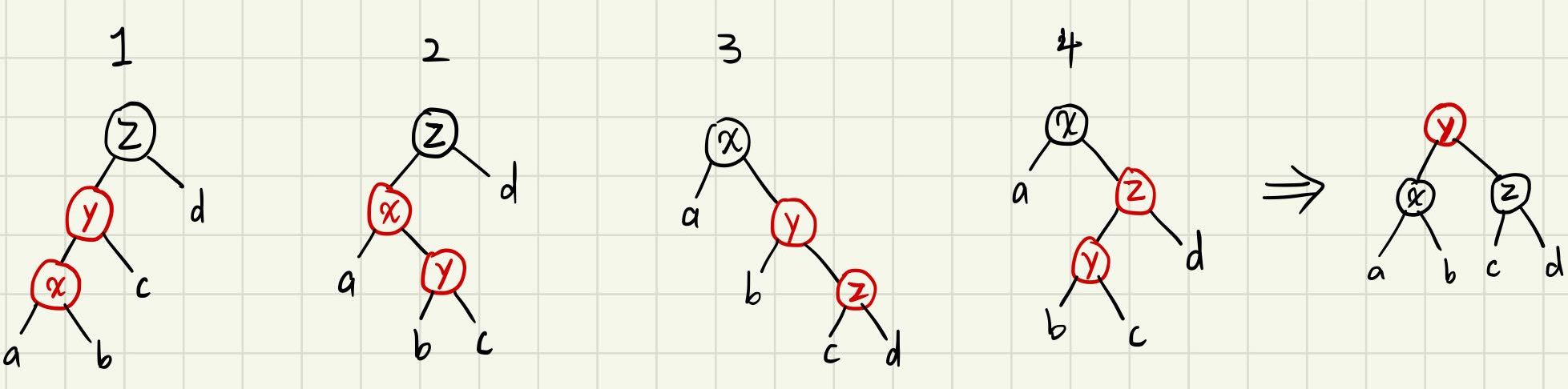
可以方便的用pattern matching來實現：

balance :: Tree a -> Tree a
balance (Node B (Node R (Node R a x b) y c) z d) = Node R (Node B a x b) y (Node B c z d)
balance (Node B (Node R a x (Node R b y c)) z d) = Node R (Node B a x b) y (Node B c z d)
balance (Node B a x (Node R (Node R b y c) z d)) = Node R (Node B a x b) y (Node B c z d)
balance (Node B a x (Node R b y (Node R c z d))) = Node R (Node B a x b) y (Node B c z d)
balance t@(Node c x l r) = t

刪除操作

插入操作只要處理“雙紅”，刪除操作還要處理“黑色節點數相等”，比較麻煩。

這里采用了Stefan Kahrs在2001年提出的方法，主要特點是：

• 不將帶刪除節點與后繼交換
• 維持一個新的invariant：
  • 從黑根子樹中刪除節點，該子樹高度會-1
  • 從紅根子樹中刪除節點，該子樹高度不變

我們有balanceL和balanceR兩個操作，分別處理“左子樹比右子樹短1”和“右子樹比左子樹短1”的情況，將整棵樹的高度變成較短那個的狀態。

刪除操作的框架如下：

delete :: Ord a => a -> Tree a -> Tree a
delete x = makeBlack . del
  where
    del Nil = Nil
    del t@(Node _ l y r) | x < y     = delL t
                         | x > y     = delR t
                         | otherwise = app l r
    delL (Node _ l@(Node B _ _ _) y r) = balanceL $ Node B (del l) y r
    delL (Node _ l y r)                = Node R (del l) y r
    delR (Node _ l y r@(Node B _ _ _)) = balanceR $ Node B l y (del r)
    delR (Node _ l y r)                = Node R l y (del r)

以待插入節點將插入左子樹為例：

• 當前節點y的左子樹為黑根時，會在刪除后將y染黑并進行balanceL操作
• 當前節點y的左子樹為紅根時，會在刪除后將y染紅

容易發現，這樣操作是可以維持新的invariant的（枚舉當前節點顏色情況證明即可）

由于delete中在balanceL/R之前會染黑，balanceL/R只要處理根為黑的情況即可，有三種情況：

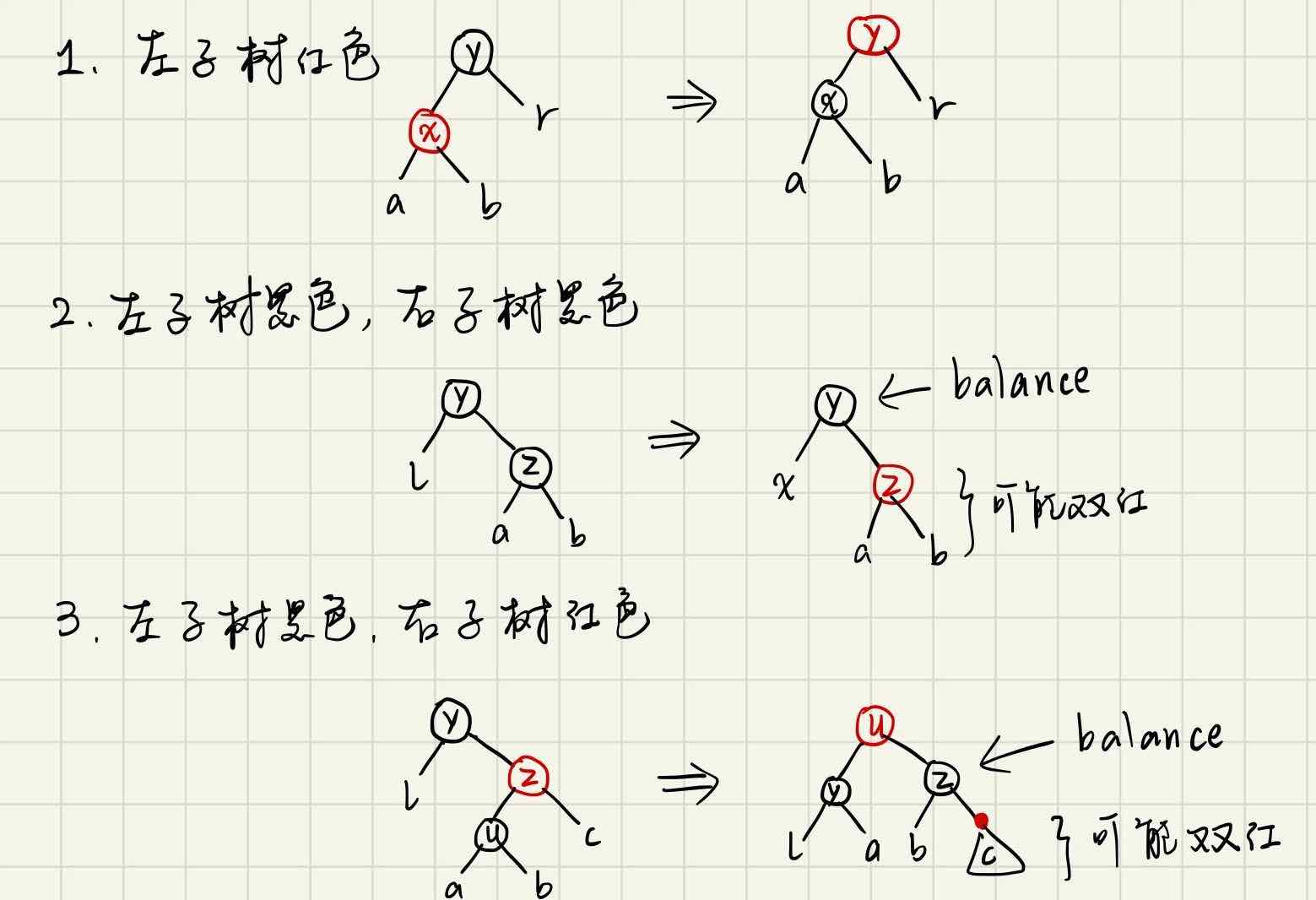同樣用pattern matching來實現：

balanceL :: Tree a -> Tree a 
balanceL (Node B (Node R a x b) y r) = Node R (Node B a x b) y r
balanceL (Node B l y (Node B a z b)) = balance $ Node B l y (Node R a z b)
balanceL (Node B l y (Node R (Node B a u b) z c)) = Node R (Node B l y a) u (balance $ Node B b z (makeRed c))

balanceR :: Tree a -> Tree a 
balanceR (Node B l y (Node R a x b)) = Node R l y (Node B a x b)
balanceR (Node B (Node B a z b) y r) = balance $ Node B (Node R a z b) y r
balanceR (Node B (Node R c z (Node B a u b)) y r) = Node R (balance $ Node B (makeRed c) z a) u (Node B b y r)

app會合并兩個子樹，有三種情況：

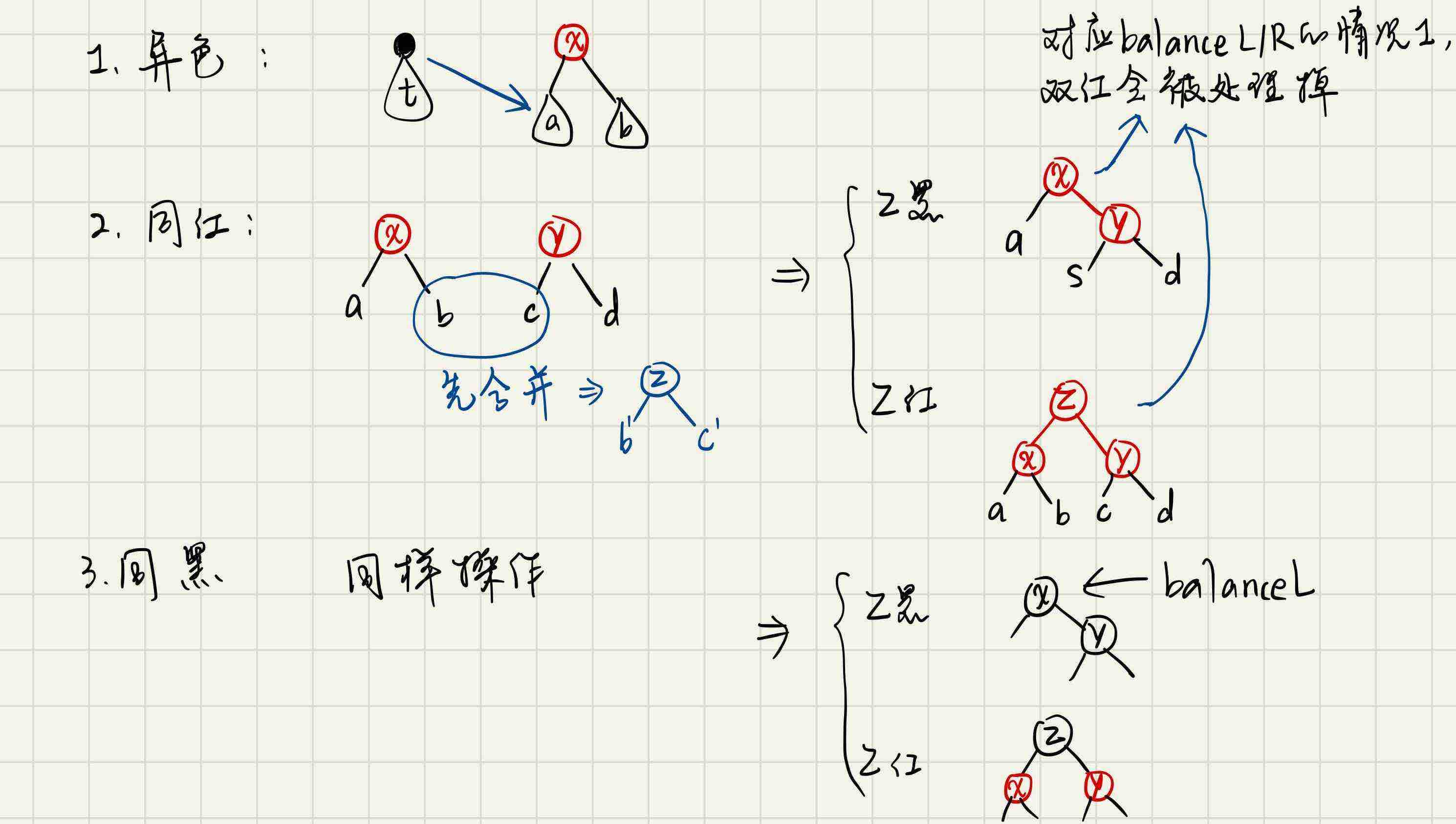
同樣用pattern matching來實現：

app :: Tree a -> Tree a -> Tree a
app Nil t = t
app t Nil = t 
app (Node R a x b) (Node R c y d) = 
  case app b c of
    Node R b' z c' -> Node R (Node R a x b') z (Node R c' y d)
    s -> Node R a x (Node R s y d)
app (Node B a x b) (Node B c y d) =
  case app b c of
    Node r b' z c' -> Node R (Node B a x b') z (Node B c' y d)
    s -> balanceL $ Node B a x (Node B s y d)
app (Node R a x b) t = Node R a x (app b t)
app t (Node R a x b) = Node R (app t a) x b

完整代碼

只要60行！

data Tree a = Nil | Node Color (Tree a) a (Tree a) deriving (Show, Eq)
data Color = R | B deriving (Show, Eq)

makeBlack :: Tree a -> Tree a
makeBlack Nil = Nil
makeBlack (Node _ l x r) = Node B l x r

makeRed :: Tree a -> Tree a
makeRed Nil = Nil
makeRed (Node _ l x r) = Node R l x r

insert :: (Ord a) => a -> Tree a -> Tree a
insert x = makeBlack . ins 
  where ins Nil = Node R Nil x Nil
        ins t@(Node c l y r) | x < y     = balance $ Node c (ins l) y r
                             | x > y     = balance $ Node c l y (ins r)
                             | otherwise = t

balance :: Tree a -> Tree a
balance (Node B (Node R (Node R a x b) y c) z d) = Node R (Node B a x b) y (Node B c z d)
balance (Node B (Node R a x (Node R b y c)) z d) = Node R (Node B a x b) y (Node B c z d)
balance (Node B a x (Node R (Node R b y c) z d)) = Node R (Node B a x b) y (Node B c z d)
balance (Node B a x (Node R b y (Node R c z d))) = Node R (Node B a x b) y (Node B c z d)
balance t@(Node c x l r) = t

delete :: Ord a => a -> Tree a -> Tree a
delete x = makeBlack . del
  where
    del Nil = Nil
    del t@(Node _ l y r) | x < y     = delL t
                         | x > y     = delR t
                         | otherwise = app l r
    delL (Node _ l@(Node B _ _ _) y r) = balanceL $ Node B (del l) y r
    delL (Node _ l y r)                = Node R (del l) y r
    delR (Node _ l y r@(Node B _ _ _)) = balanceR $ Node B l y (del r)
    delR (Node _ l y r)                = Node R l y (del r)

balanceL :: Tree a -> Tree a 
balanceL (Node B (Node R a x b) y r) = Node R (Node B a x b) y r
balanceL (Node B l y (Node B a z b)) = balance $ Node B l y (Node R a z b)
balanceL (Node B l y (Node R (Node B a u b) z c)) = Node R (Node B l y a) u (balance $ Node B b z (makeRed c))

balanceR :: Tree a -> Tree a 
balanceR (Node B l y (Node R a x b)) = Node R l y (Node B a x b)
balanceR (Node B (Node B a z b) y r) = balance $ Node B (Node R a z b) y r
balanceR (Node B (Node R c z (Node B a u b)) y r) = Node R (balance $ Node B (makeRed c) z a) u (Node B b y r)

app :: Tree a -> Tree a -> Tree a
app Nil t = t
app t Nil = t 
app (Node R a x b) (Node R c y d) = 
  case app b c of
    Node R b' z c' -> Node R (Node R a x b') z (Node R c' y d)
    s -> Node R a x (Node R s y d)
app (Node B a x b) (Node B c y d) =
  case app b c of
    Node r b' z c' -> Node R (Node B a x b') z (Node B c' y d)
    s -> balanceL $ Node B a x (Node B s y d)
app (Node R a x b) t = Node R a x (app b t)
app t (Node R a x b) = Node R (app t a) x b

其他API

一些其他常規操作的API：

tree2List :: Tree a -> [a]
tree2List Nil = []
tree2List (Node c l x r) = tree2List l ++ [x] ++ tree2List r

list2Tree :: Ord a => [a] -> Tree a
list2Tree = foldl (flip insert) Nil 

search :: (Ord a) => a -> Tree a -> Bool
search _ Nil = False
search x (Node _ l y r) 
  | x == y    = True
  | x < y     = search x l
  | otherwise = search x r

successor :: Ord a => a -> Tree a -> a
successor x Nil = x
successor x (Node _ l y r) 
  | x <  y = let t = successor x l in if x == t then y else t
  | x >= y = successor x r

PS：因為沒有維護size信息所以沒法求第k小QwQ，不過加上size信息應該也不難寫。

參考資料

• 一篇講的很好的博客
• 一份代碼實現
• Kahrs, Stefan. (2001). Red-black trees with types. Journal of Functional Programming. 11. 10.1017/S0956796801004026.

另外，Matt Might提出了一種更加簡潔、函數式的方法，詳情參閱他的博客。