圖形學
圖形學就是在一個二維的平面上展示三維模型.
這里我們用H5的canvas來演示. 我們不會用canvas的任何畫圖的方法, 只是把他當作一個屏幕來使用.
三維模型
要將三維物體,表現在二維平面上, 首先我們要有一個三維的模型.我們要先知道,如何在一個三維坐標系中構造一個物體的模型.
這個模型是怎么做的呢. 他一般包含一下幾點
中心點和旋轉角度.
中心點一般用來確定一個模型在三維坐標系中的具體位置. 一般用 x, y, z 表示.中心點移動, 模型上的所有坐標跟著移動. 模型旋轉時,繞中心點旋轉.
三角形網絡 和 頂點.
模型的具體形狀是由三角形拼成的. 如圖所示
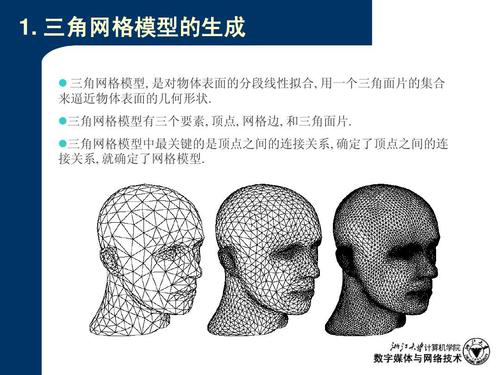
所有的模型都是有一個一個三角形拼成的. 三角形少, 精度就小.三角形多,精度就大. 也就越接近顯示中的物體. 以一個正方體為例, 6個面, 一個面需要兩個三角形拼成, 一共12個三角形.
三角形的點就是頂點. 一般有很多三角形的頂點是重復的. 立方體一共八個頂點. 代碼實踐中我們是頂點做一個數組. 三角形做一個數組.
let points = [
-1, 1, -1, // 0
1, 1, -1, // 1
-1, -1, -1, // 2
1, -1, -1, // 3
-1, 1, 1, // 4
1, 1, 1, // 5
-1, -1, 1, // 6
1, -1, 1, // 7
]
let vertices = []
for (let i = 0; i < points.length; i += 3) {
let v = GuaVector.new(points[i], points[i+1], points[i+2])
// let c = GuaColor.randomColor()
let c = GuaColor.red()
vertices.push(GuaVertex.new(v, c))
}
// 12 triangles * 3 vertices each = 36 vertex indices
let indices = [
// 12
[0, 1, 2],
[1, 3, 2],
[1, 7, 3],
[1, 5, 7],
[5, 6, 7],
[5, 4, 6],
[4, 0, 6],
[0, 2, 6],
[0, 4, 5],
[5, 1, 0],
[2, 3, 7],
[2, 7, 6],
]
在上述代碼中, points就是頂點的數組, 每三個元素是一組坐標,表示該頂點的x,y,z.
indices是三角形的數組, 第一個元素[0, 1, 2] 表示第一個三角形. 這里的0表示 頂點數組里的第0個頂點.
頂點的屬性.
頂點的屬性包括,坐標(x, y, z), 顏色(rgba), 法向量(fx, fy, fz), 貼圖.
- 坐標就是這個點在三維坐標系中的坐標.
- 顏色就是rgba顏色.
- 法向量就是這個點的垂直方向. 法向量屬性這里和我們的數學嘗試有些區別. 一個點為什么會有法向量呢?
原因在于我們這里的頂點并不是數學意義上的點. 數學上的點是沒有大小,寬高,方向的. 但是我們這里的頂點有. 嚴格意義上來說 這里的頂點是一個長寬都是1像素的面,是面的最小組成單元 .他有坐標, 有寬高都是1,既然是面當然有法向量. 又因為他足夠小.能夠近似的看做點. - 貼圖. 貼圖指的是, 這個模型的顏色不是單一的顏色, 而是一張圖. 一般會有一個貼圖文件. 貼圖文件里保存的是每一個頂點上應該填充的顏色. 頂點的貼圖屬性里保存的就是這個顏色值在貼圖文件中的位置.
視角
視角就是三維空間中我們觀察模型時的視線. 視角有三個屬性.
- position: 視角的坐標,就是眼睛的坐標
- target: 我們的視角觀察的目標的坐標. position和target連起來就是視線
- up: 是position到target的距離.
這三個屬性確定一個視角. 視角移動的話, 三維模型的投影也會發生變化.
光照陰影
光照陰影(shading). 在二維坐標系中模擬顯示中的物體還要考慮光照問題. 我們看到的顏色是物體反射光的顏色. 光線照射到物體上的角度不同, 物體上光線的強度就不同.
就是有一個光源, 他發射除了光線, 光線照射到 物體上, 由于角度不同導致了, 雖然物體上的顏色相同, 但是看起來顏色有區別, 有高光, 有陰影.比如物體模型是紅色, 光線與三角形是垂直關系90°展示正紅色, 不是垂直是60°, 是暗紅色, 隨著角度越來越小,顏色越來越暗. 也就是說點的顏色要根據法向量和光線的夾角來計算.
根據計算方式不同, 會有不同效果.
如下圖所示

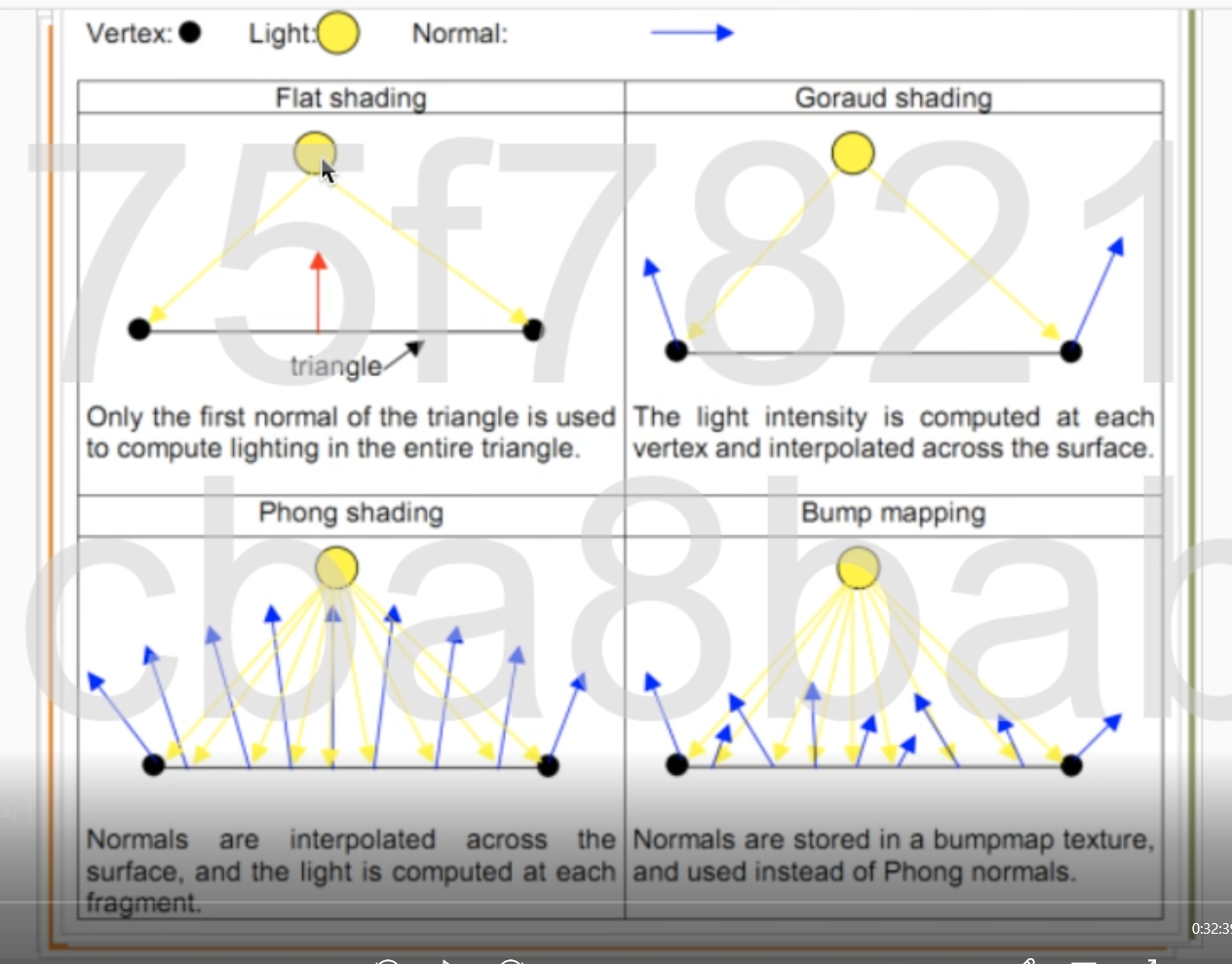
這是不同的光照模型和不同精度下模型的效果. 從上到下是精度越來越高, 從左到右是 光照的計算越來越精細.
- 左1(a1), (flat shading)是一個三角形用一個法向量, 所以一個平面的光照是一樣的.
- 左2(b1),(goraud shading) 是一個頂點一個法向量, 一個三角形就有三個法向量. 其他點用頂點的光照計算插值.
- 左3(c1), (phong shading) 是先 一個頂點一個法向量, 然后,用這三個頂點的法向量 插值計算其他點的法向量, 然后再計算光照. 所以c1即便模型精度很低, 但是也依然有了一個精度相對高的光照.
這是不同光照下的法向量方向.
二維平面
像素
要在二維平面上展示圖像, 基礎是畫點. 一張圖片是由像素組成的. 比如 一張分辨率為50*100的png圖片. 那么這張圖長寬有50個像素, 高有100個像素.像素就是圖片最基礎的組成單元. 所有的圖片都是由像素組成.
像素的屬性包括: 坐標x, y表示像素的位置. rgba表示像素的顏色.比如紅色用rgba表示就是(255, 0, 0, 255). rgba的每一個值都是0-255. 用二進制表示剛好一個字節的數據量.
以H5中的canvas圖片的像素為例.
var c=document.getElementById("myCanvas");
var ctx=c.getContext("2d");
ctx.fillStyle="red";
ctx.fillRect(0, 0, 50, 50);
// 獲取canvas上的像素數據. 參數(x, y, w, h)
var imgData=ctx.getImageData(0, 0, 50, 50);
imgData.data[1] = 255
ctx.putImageData(imgData,10,10);
// 使用putImageData之后, 會直接改變canvas上的像素顏色.
這里的imgData就是canvas中的像素數據. 格式如下
{
height: 50,
width: 50,
data: [
255, 0,0, 255,
255, 0,0, 255,
255, 0,0, 255,
......
]
}
這里的imgData表示這張canvas圖片, 高50像素, 寬50像素. data里面的數據是從左上角開始,從左到右, 從上到下依次排列. 每4個元素表示該像素的顏色信息. 比如第一個像素的rgba是(255, 0, 0, 255).
一共由 50 * 50 = 2500個像素, 每個像素用4個數據表示顏色. 所以在data里由10000個元素.
所以只要我們有了一張圖的像素信息, 就能直接把這張圖展示出來.
光柵化
我們現在有了一個三維的立體模型, 屏幕是二維的, 要在一個二維屏幕上展示三維圖形, 就需要把三維圖形投影到二維平面上, 用像素展示出來, 稱為為光柵化.
比如:

上圖就是一個立方體在二維平面中的投影. 如果我們轉變觀察這個立方體的角度, 這個投影的形狀也會發生改變. 從三維立體圖形, 到二維平面的投影圖, 我們可以通過三角函數計算, 獲得最終的尺寸. 那么針對一個三維模型, 我們要考慮他的旋轉角度, 相對于遠點的位移, 觀察的視角, 以及投影面. 這些都考慮到后, 我們就能得到一個貼近于真是的投影圖.
矩陣
上面說了, 要從三維模型的坐標, 考慮很多條件, 用三角函數來計算出最終投影到平面上的二維坐標. 但是這樣一個個計算太過復雜, 一般都是通過矩陣來直接計算的. 矩陣能將三維模型的坐標點, 直接轉換成要投影的二維坐標, 常用的矩陣包括:
- 計算旋轉角度的旋轉矩陣rotation
- 計算模型位移的位移矩陣translation
- 確認觀察視角的視角矩陣view
- 把三維坐標轉換成二維坐標的投影矩陣projuction
矩陣是跟著模型走的, 一個單獨的模型, 比如說房間里的一張床, 一個桌子, 當他移動的時候, 所有的點都跟著移動. 當他旋轉的時候, 所有的點都跟著旋轉.這個模型有一個中心點和旋轉角度來確定他在三維空間的位置, 比如水平旋轉了30°, 根據中心點, 和 旋轉角度, 一個桌子上的點就能算出旋轉后的位置, 旋轉矩陣就是做這個地, 位移矩陣就是計算當中心點移動了10個像素后, 其他點的位置. 旋轉矩陣和位移矩陣是計算模型在移動后的三維空間的坐標, 視角矩陣是當三維空間的視角變化后, 模型在三維空間的坐標變化. 投影矩陣是將三維坐標轉換成二維坐標.
// 視角矩陣
const view = Matrix.lookAtLH(position, target, up)
// 投影矩陣
const projection = Matrix.perspectiveFovLH(0.8, w / h, 0.1, 1)
// 得到 mesh 中點在世界中的坐標
const rotation = Matrix.rotation(mesh.rotation) //旋轉矩陣
const translation = Matrix.translation(mesh.position) //位移矩陣
const world = rotation.multiply(translation) // 世界矩陣
// transform就是最后的矩陣.
const transform = world.multiply(view).multiply(projection)
矩陣可以相乘, 相乘的效果與依次使用是一樣的.
深度
一個三維模型投影到二維平面, 因為我們看到是投影, 看到正面的話,就不能看到背面. 而且正面和背面雖然在二維平面的坐標是一樣的, 但是顏色是不一樣的. 那么我們怎么確定具體畫哪個點呢?
就用深度.
一個三維的頂點經過矩陣計算后得到的除了x,y二維坐標, 還有一個深度. 這個深度是和視角的距離. 如果和視角的距離近, 那么就展示,如果相對較遠, 就不畫. 一般來說是保存一個 二維平面上已經畫好的點的數組 .這個點的信息就包括他在二維平面上的坐標,顏色,深度. 再畫點時, 先判斷這個點的坐標是否已經畫過了, 如果沒有,就畫上. 如果畫過了, 對比深度.如果當前點的深度更近,就把原來的覆蓋掉, 否則不畫.
插值
我們的圖形是以三角形為基礎的, 圖像信息都是存儲在頂點上的, 頂點上的坐標, 顏色都有了, 但是我們不能只畫頂點, 那么兩個頂點之間的點的圖像信息是怎么得到的呢?
就是用插值計算得到的.
比如說有兩個點.
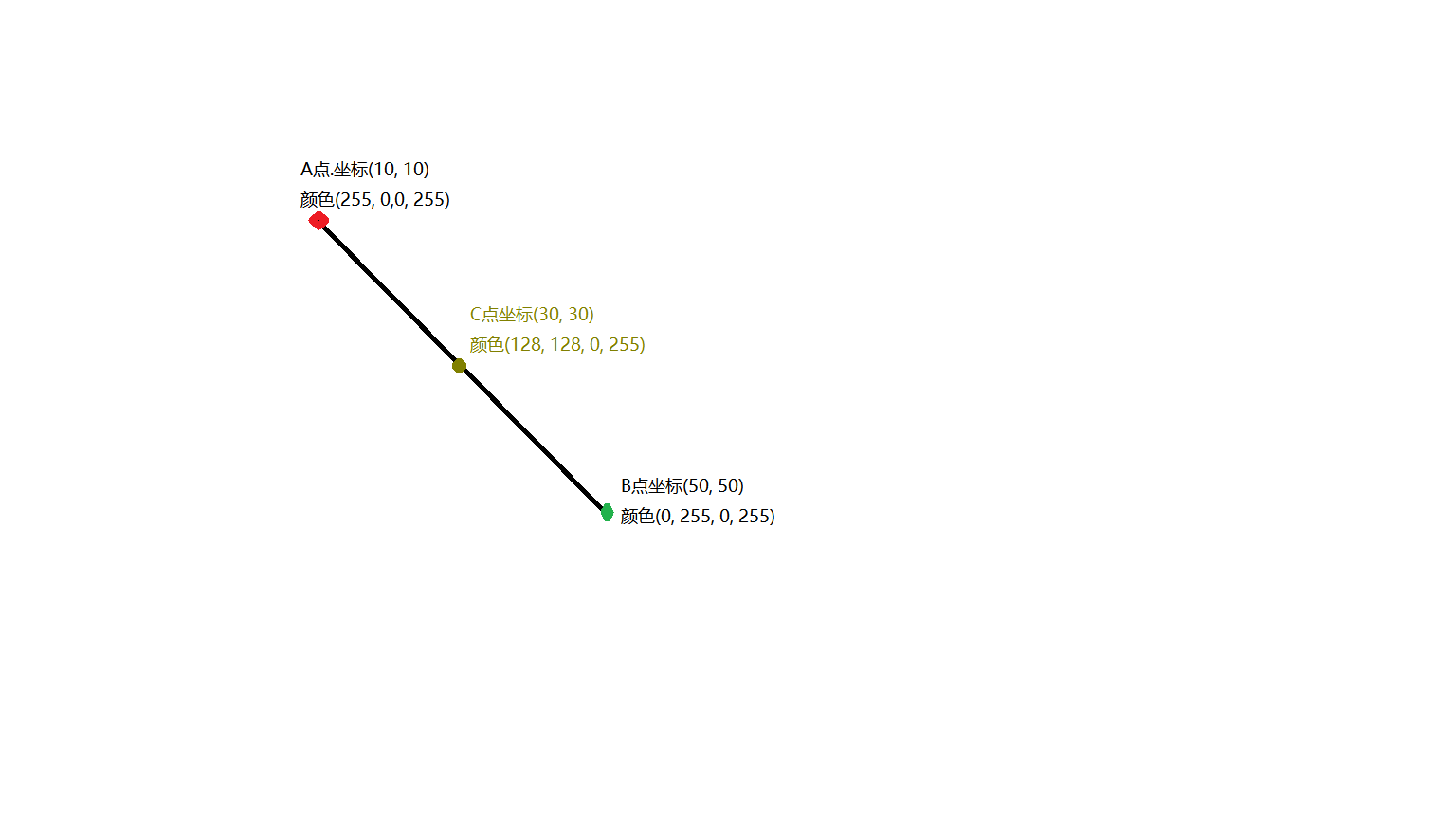
- A點,坐標(10, 10).顏色紅色(255, 0, 0, 255)
- B點, 坐標(50, 50). 顏色綠色(0, 255, 0, 255)
現在要問處于這兩點之間的C點的顏色和坐標.
首先計算factor, 過渡因子.
首先計算AB的長度.
var x1 = 10, y1 = 10, x2 = 50, y2 = 50
// 長度s
var s = ( (x2 - x1) ** 2 + (y2 - y1) ** 2 ) ** 0.5
// 假設我們要畫AB上距離A點10像素的點, 根據點距A的距離占總距離的比例,計算到他的坐標
var factor = 10 / s
var x = factor * (x2 - x1) + x1
var y = factor * (y2 - y1) + y1
顏色的插值計算與坐標一樣.
C點是AB的中心點, 那么C的坐標就是(30, 30), 顏色(128, 128, 0, 255).所有的計算中有小數的四舍五入.
畫線就是把AB兩點之間的所有的點, 根據這個點的所在位置,計算插值, 然后把所有的點都畫出來.
畫三角形
現在二維平面上的三角形點的信息有了, 根據插值我們能畫線了. 那么三角形這個面怎么畫呢?
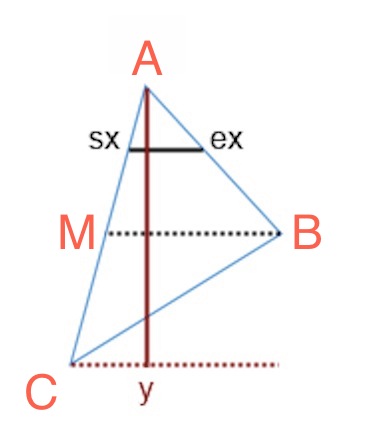
首先我們有三角形的三個頂點A B C按Y軸坐標排列, a.y > b.y > c.y.
對AC邊求得M點(m.y == b.y). 三角形就被劃分成了AMB, MBC兩個三角形.
然后先畫AMB.
從上到下, 從A點開始畫平行線. 根據距離A點的高度, 算出factor,計算插值, 然后找出AM上的sx點和 AB上的ex點. sx-ex線與MB平行. 這算是在AMB三角形中填了一條線. 然后再用平行線一條一條把整個AMB填滿, 從上到下, 如果A距離MB的高度為10, 那就是10條線.
AMB畫完了再畫MBC.
一個三角形畫完了, 把所有的三角形都畫完.整個立體圖形就都出來了.



 浙公網安備 33010602011771號
浙公網安備 33010602011771號