optimization失敗解決辦法
三個臨界點
一、critical point(臨界點 / 駐點)
在多元函數 \(f(x1,x2,…,xn\))中,
臨界點(critical point) 是指:
也就是所有偏導數都為 0 的點。
?? 這些點可能是:
- 局部極小值點(local minimum)
- 局部極大值點(local maximum)
- 鞍點(saddle point)
所以 臨界點是一個集合的上位概念,它包含了后兩種情況。
二、local minima(局部極小值)
定義:
點$ x^* $是局部極小值點,當存在一個足夠小的鄰域 \(U\),
對所有 \(x∈U\),都有:
\(f(x?)≤f(x)\)
?? 在這個點附近,函數值都是比它高的。
(但可能還有更低的全局最小值)
在一元函數里,這個點的特征是:
\(f′(x?)=0,f′′(x?)>0\)
在多元函數中:
\(?f(x?)=0,H(x?)\)(Hessian矩陣)正定
三、saddle point(鞍點)
定義:
點\(x^*\) 也是臨界點(梯度為 0),
但是在某些方向上函數值比它大,某些方向上比它小。
也就是說:
\(??u,v:f(x?+u)>f(x?),f(x?+v)<f(x?)\)
它既不是極大,也不是極小。
在多元函數中:
\(?f(x?)=0,H(x?)\)有正有負特征值(不定矩陣)
四、直觀對比
| 類型 | 梯度條件 | Hessian條件 | 函數形狀 | 示例 |
|---|---|---|---|---|
| local minimum | \(?f=0\) | 正定 | 碗口向上 | \(f(x,y)=x2+y2\) |
| local maximum | \(?f=0\) | 負定 | 碗口向下 | \(f(x,y)=?x2?y2\) |
| saddle point | \(?f=0\) | 不定 | 鞍形 | \(f(x,y)=x2?y2\) |
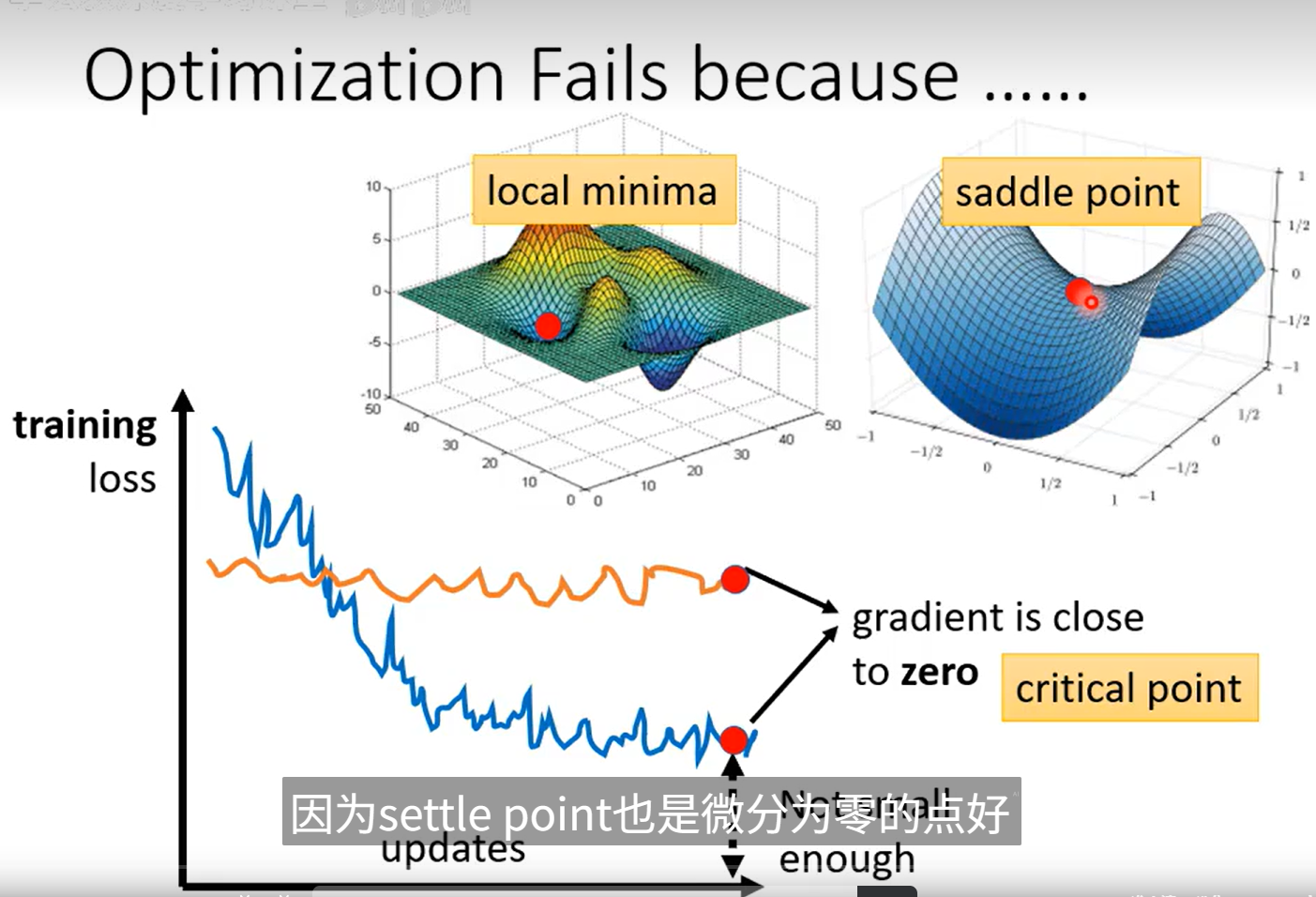
方法一:Hessian 與臨界點類型判斷
在臨界點 $( theta' ) \(處,梯度為 0: \)\nabla L(\theta') = 0$
根據二階泰勒展開:
\(L(\theta) \approx L(\theta') + \frac{1}{2}(\theta - \theta')^T H (\theta - \theta')\)
其中 ( H ) 是 Hessian 矩陣。
判斷規則
| 條件 | Hessian 性質 | 結論 |
|---|---|---|
| 對所有 (v),(v^T H v > 0) | 正定 | 局部極小值(Local Minima) |
| 對所有 (v),(v^T H v < 0) | 負定 | 局部極大值(Local Maxima) |
| 有的 (v^T H v > 0),有的 (v^T H v < 0) | 不定 | 鞍點(Saddle Point) |
?? 總結:
臨界點處梯度為零;
Hessian 的符號決定了函數曲面的形態。

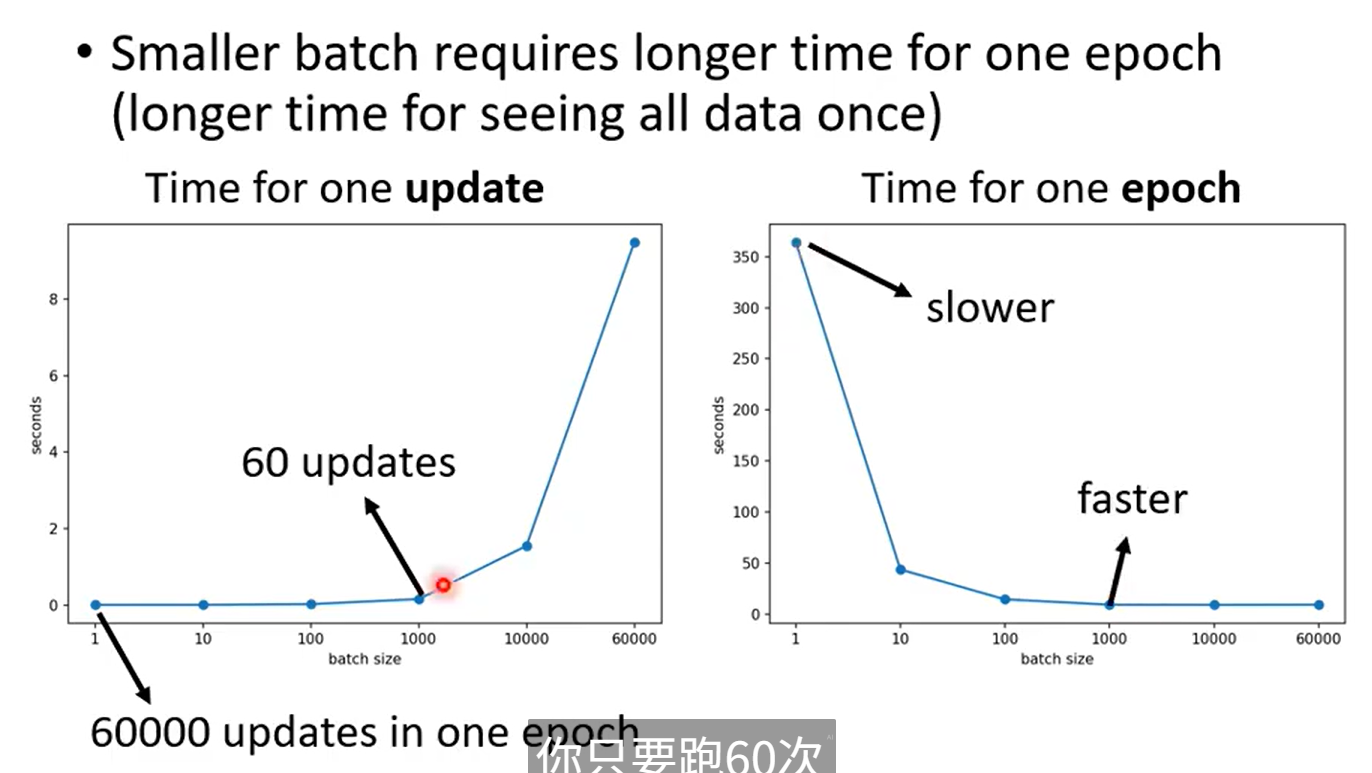
方法二:Batch 和 Momentum
small Batch 和 large Batch 的優劣:
速度(GPU并行計算);
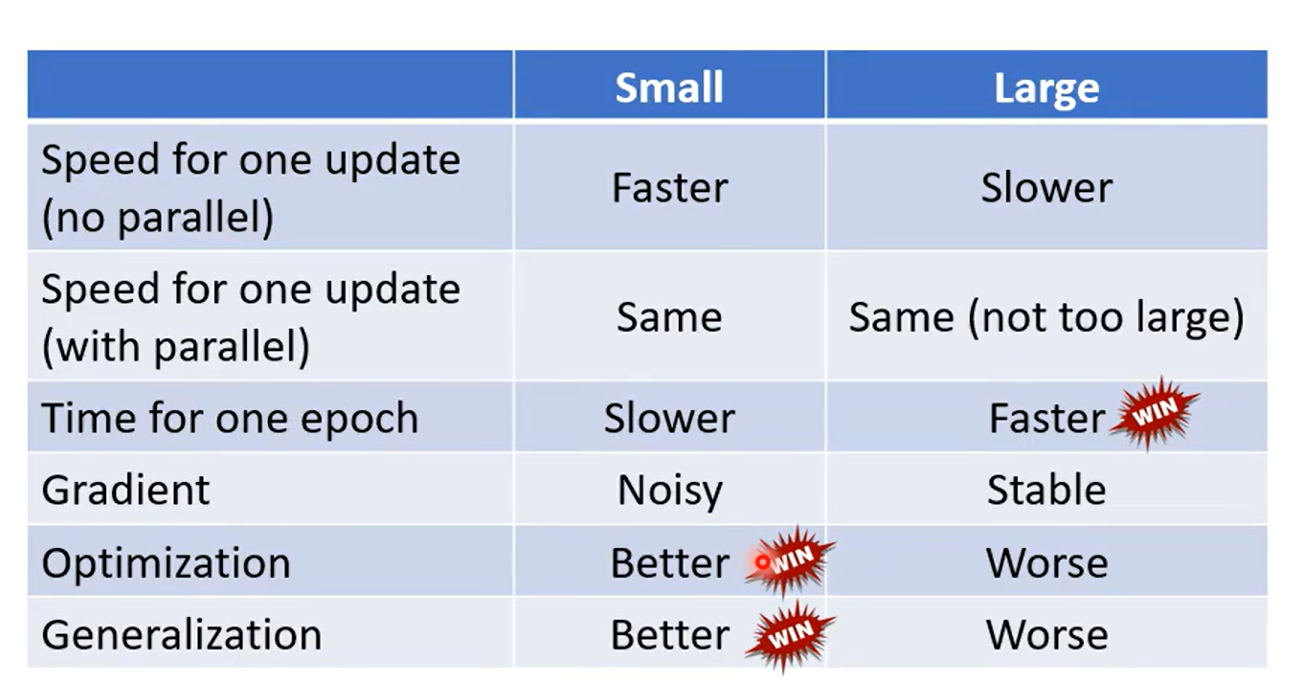
不是 Batch 越大越好,也不是越小越好
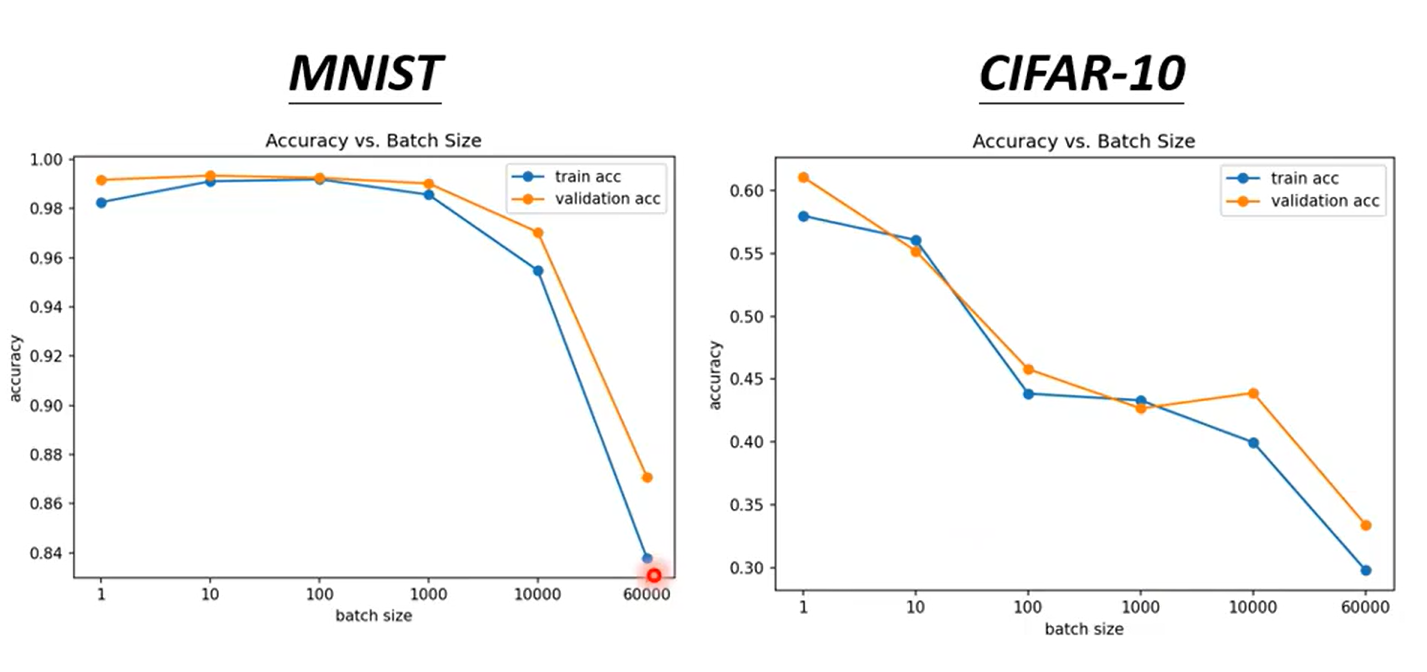
驗證集正確率:
**validation generated set(驗證集)**
Batch 越大,帶來的結果可能越差
這個是 optimization 的問題
優勢比較
Momentum
梯度(Gradient):就是函數在某一點處,變化最快的方向和變化率。
一般的 Gradient
每次更新沿著梯度的反方向
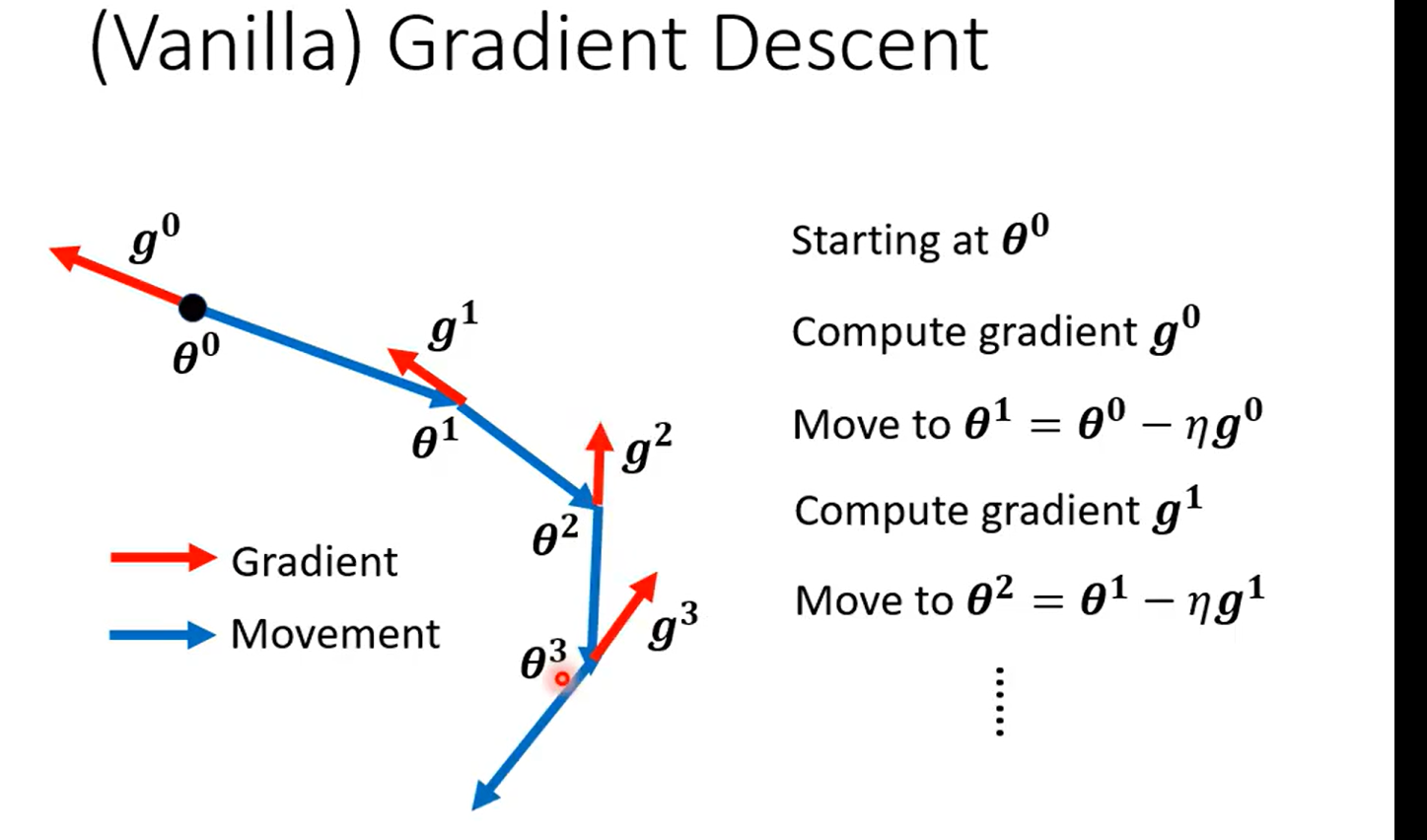
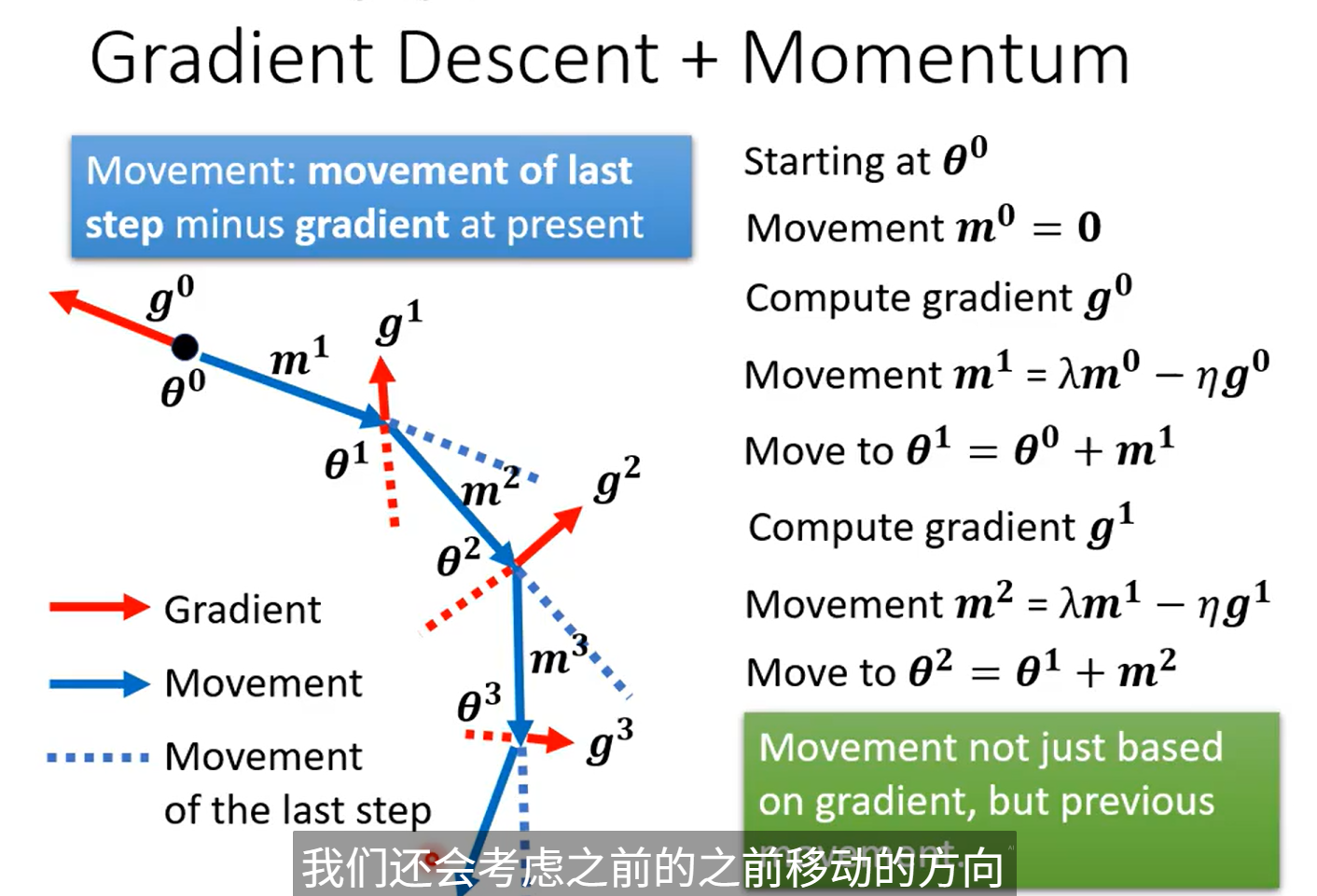
Momentum 的 Gradient(有慣性的更新)
每次更新沿著梯度的反方向和上一次的影響



 浙公網安備 33010602011771號
浙公網安備 33010602011771號