在計算機中采用科學記數(shù)法將浮點數(shù)分為下面三部分：

float 4個字節(jié) 32位 從高到低依次是：

舉例：十進制的小數(shù)20.1如何轉成計算機中的存儲形式（二進制）呢？

步驟：

• 整數(shù)部分和小數(shù)部分分別轉成二進制
  • 整數(shù)部分轉二進制：除2取余，拿整數(shù)部分除2，每次操作記下余數(shù)，然后拿商繼續(xù)除2，直到商為0；最后將每一步求得的余數(shù)倒序排列。
  • 小數(shù)部分轉二進制：乘2取整，拿小數(shù)部分即0.xxx乘2，每次操作結果留整數(shù)部分，接下來繼續(xù)拿小數(shù)部分乘2，直到小數(shù)部分為0；最后將每步求得的整數(shù)部分正序排列。
• 移位成標準的科學記數(shù)法，即：

• 讓指數(shù)+127
• 取小數(shù)部分位前23位，不足23位后面補0，超過23位只取前23位

實戰(zhàn)：

第一步：分別將整數(shù)和小數(shù)部分轉成二進制

對于20轉二進制：

• 20/2 商10 余0
• 10/2 商5 余0
• 5/2 商2 余1
• 2/2 商1 余0
• 1/2 商0 余1 ??

所以二進制存儲形式：10100

對于0.1轉二進制

• 0.1*2 得0.2 整數(shù)部分0 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 0.2*2 得0.4 整數(shù)部分0 接下來拿小數(shù)部分0.4繼續(xù)乘2
• 0.4*2 得0.8 整數(shù)部分0 接下來拿小數(shù)部分0.8繼續(xù)乘2
• 0.8*2 得1.6 整數(shù)部分1 接下來拿小數(shù)部分0.6繼續(xù)乘2
• 0.6*2 得1.2 整數(shù)部分1 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 0.2*2 得0.4 整數(shù)部分0 接下來拿小數(shù)部分0.4繼續(xù)乘2
• 0.4*2 得0.8 整數(shù)部分0 接下來拿小數(shù)部分0.8繼續(xù)乘2
• 0.8*2 得1.6 整數(shù)部分1 接下來拿小數(shù)部分0.6繼續(xù)乘2
• 0.6*2 得1.2 整數(shù)部分1 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 0.2*2 得0.4 整數(shù)部分0 接下來拿小數(shù)部分0.4繼續(xù)乘2
• 0.4*2 得0.8 整數(shù)部分0 接下來拿小數(shù)部分0.8繼續(xù)乘2
• 0.8*2 得1.6 整數(shù)部分1 接下來拿小數(shù)部分0.6繼續(xù)乘2
• 0.6*2 得1.2 整數(shù)部分1 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 0.2*2 得0.4 整數(shù)部分0 接下來拿小數(shù)部分0.4繼續(xù)乘2
• 0.4*2 得0.8 整數(shù)部分0 接下來拿小數(shù)部分0.8繼續(xù)乘2
• 0.8*2 得1.6 整數(shù)部分1 接下來拿小數(shù)部分0.6繼續(xù)乘2
• 0.6*2 得1.2 整數(shù)部分1 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 0.2*2 得0.4 整數(shù)部分0 接下來拿小數(shù)部分0.4繼續(xù)乘2
• 0.4*2 得0.8 整數(shù)部分0 接下來拿小數(shù)部分0.8繼續(xù)乘2
• 0.8*2 得1.6 整數(shù)部分1 接下來拿小數(shù)部分0.6繼續(xù)乘2
• 0.6*2 得1.2 整數(shù)部分1 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 0.2*2 得0.4 整數(shù)部分0 接下來拿小數(shù)部分0.4繼續(xù)乘2
• 0.4*2 得0.8 整數(shù)部分0 接下來拿小數(shù)部分0.8繼續(xù)乘2
• 0.8*2 得1.6 整數(shù)部分1 接下來拿小數(shù)部分0.6繼續(xù)乘2
• 0.6*2 得1.2 整數(shù)部分1 接下來拿小數(shù)部分0.2繼續(xù)乘2
• 可以看到已經開始無限循環(huán)了 下面的計算省略

所以0.1轉成二進制，是一個無限循環(huán)小數(shù)，即：00011001100110011001100.....

第二步：移位成標準記數(shù)法

即：10100. 00011001100110011001100110011.... * 2^0

變成：1. 0100 00011001100110011001100110011...*2^4

第三步：指數(shù)部分處理

4+127=131 ,131轉二進制，10000011

小數(shù)部分取前23位，不夠的末尾補0，超出的截斷--這也就是浮點數(shù)存在誤差的由來

01000001100110011001101（最后這個1是四舍五入來的）

第四步：整合最后結果

0（符號位）10000011（指數(shù)位）01000001100110011001101（小數(shù)位）
0 10000011 01000001100110011001101

轉換成16進制：

轉換為十六進制（每 4 位一組）：
0100 0001 1010 0000 1100 1100 1100 1101 → 0x41A0CCCD

在編譯器中驗證

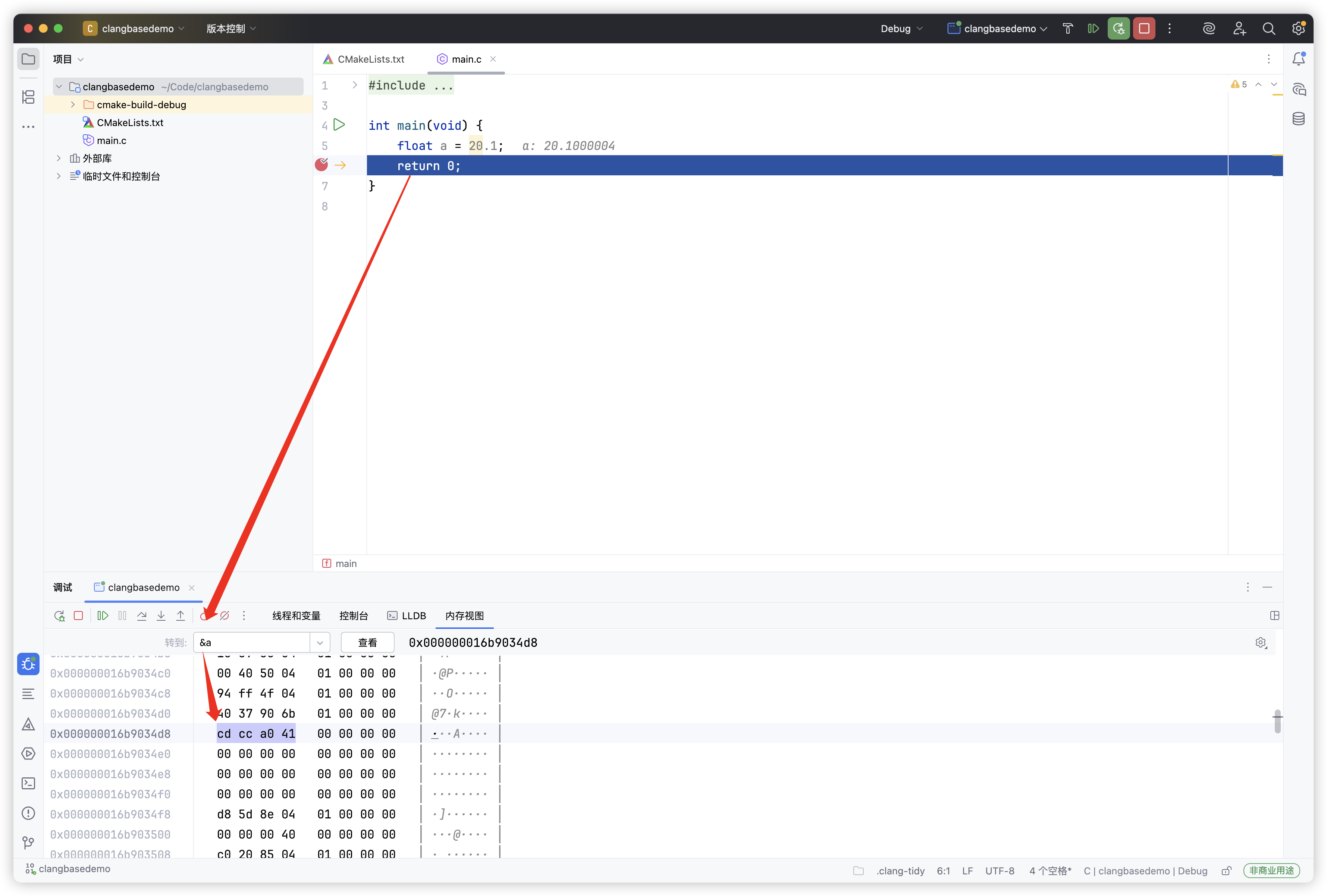
由于是小端存儲，所以我們的計算結果其實是對的上的。關于大小端可以看我的這篇博客：C 大端存儲與小端存儲

參考：

在線進制轉換工具

0.5轉換成二進制

十進制小數(shù)轉化為二進制小數(shù)

浮點數(shù)的十進制和二進制轉換（詳細例子解答）