#### 棋盤覆蓋問題可視化動圖——python

棋盤覆蓋問題是一個經(jīng)典的分治法解決的問題，具體內(nèi)容可以參照以下博主的解析

棋盤覆蓋算法解析

為了更好的理解該算法分治的過程

利用了python中的matplotlib庫進(jìn)行了該算法的可視化

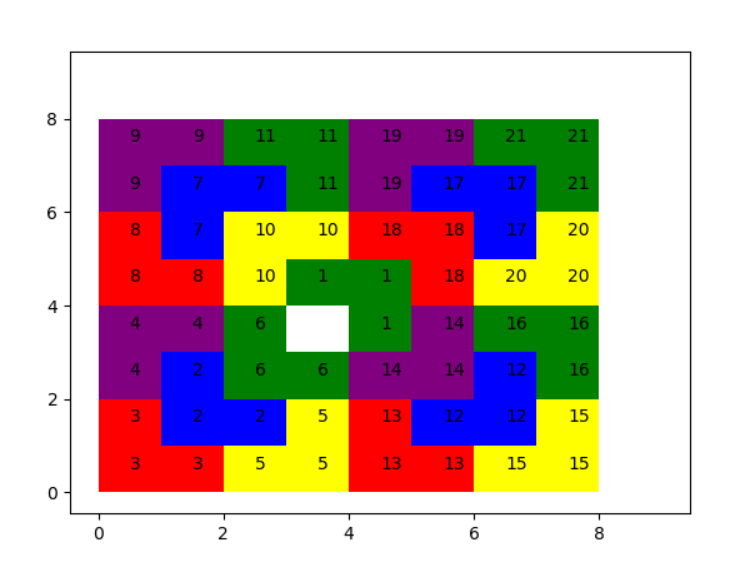
具體動畫可復(fù)制代碼在本地運(yùn)行查看

import matplotlib.pyplot as plt 
import numpy as np 

count=0
color=['yellow','green','blue','red','purple'] #顏色數(shù)組


def fill(x,y,t):

    xx=np.linspace(x,x+1,10)
    yy=np.linspace(y,y,10)
    yy1=np.linspace(y+1,y+1,10)
    plt.fill_between(xx,yy,yy1,facecolor=color[t%(len(color))]) #填充
    plt.text(x+0.5,y+0.5,t) #添加文字
    plt.pause(1) #動態(tài)畫圖 參數(shù)為變化的時間
    pass 


def ChessBoard(tr,tc,dr,dc,size):
    if size==1:  #算法實(shí)現(xiàn)
        return 
    global count
    global Board 
    count+=1
    t=count
    s=size//2
    if dr<tr+s and dc<tc+s:
        ChessBoard(tr,tc,dr,dc,s)
    else:
        Board[tr+s-1][tc+s-1]=t
        fill(tr+s-1,tc+s-1,t)
        ChessBoard(tr,tc,tr+s-1,tc+s-1,s)
    
    if dr<tr+s and dc>=tc+s:
        ChessBoard(tr,tc+s,dr,dc,s)
    else:
        Board[tr+s-1][tc+s]=t
        fill(tr+s-1,tc+s,t)
        ChessBoard(tr,tc+s,tr+s-1,tc+s,s)

    if dr>=tr+s and dc<tc+s:
        ChessBoard(tr+s,tc,dr,dc,s)
    else:
        Board[tr+s][tc+s-1]=t
        fill(tr+s,tc+s-1,t)
        ChessBoard(tr+s,tc,tr+s,tc+s-1,s)

    if dr>=tr+s and dc>=tc+s:
        ChessBoard(tr+s,tc+s,dr,dc,s)
    else:
        Board[tr+s][tc+s]=t
        fill(tr+s,tc+s,t)
        ChessBoard(tr+s,tc+s,tr+s,tc+s,s)

def pre():
    x=2**n
    y=2**n
    xx=np.linspace(x,x+1,10)
    yy=np.linspace(y,y,10)
    yy1=np.linspace(y+1,y+1,10)
    plt.fill_between(xx,yy,yy1,facecolor='white') 
    plt.pause(1)
    pass 

n=int(input())
Board=[[0 for i in range(2**n)] for j in range(2**n)]
x,y=map(int,input().split())
pre() #圖像預(yù)處理
Board[x][y]=-1
ChessBoard(0,0,x,y,2**n)
for i in range(2**n):
    for j in range(2**n):
        print(Board[i][j],end=' ')
    print()

plt.show()
# n為正方形的階數(shù) x y為方格點(diǎn)的坐標(biāo)