在x86和ARM平臺上，整數(shù)除法是相對較慢的操作。不巧的是除法在日常開發(fā)中使用頻率并不低，而且還有一些其他常用的運算依賴于除法操作，比如取模。因此頻繁的除法操作很容易成為程序的性能瓶頸，尤其是在一些數(shù)值計算程序里。

人們當(dāng)然也想了很多辦法優(yōu)化，比如在除數(shù)是2的冪的時候，除法可以用速度更快的位運算來替換。比較新的編譯器都會自動進行這類優(yōu)化。然而不是所有的除數(shù)都是2的冪，也不是所有表達(dá)式里的除數(shù)在編譯期間可知，因此我們還需要一些別的手段。

libdivide就是這樣一種整數(shù)除法的優(yōu)化手段，它不僅能應(yīng)用前面提到的位運算優(yōu)化，它還可以在運行時根據(jù)除數(shù)和被除數(shù)的特性選擇速度最快的算法來模擬除法操作，最有意義的地方在于如果硬件平臺支持SIMD指令，它還會在條件允許下盡量使用SSE2/AVX2/AVX256/NEON等SIMD指令做優(yōu)化，重復(fù)發(fā)揮了現(xiàn)代cpu的性能優(yōu)勢。按照項目文檔的說法，在有SIMD的加持下，64位整數(shù)的除法運算最大可以提升10倍。

libdivide是個頭文件庫，這意味著只需要簡單包含一下它提供的頭文件就可以使用了，不需要額外的編譯和安裝。同時它的使用方法也很簡單，庫做了運算符重載，只要初始化一下它需要的對象就可以了：

int64_t a = 1000;
libdivide::divider<int64_t> fast_d(10);
int64_t result = a / fast_d;
a /= fast_d;

c語言沒有提供運算符重載的功能，因此得用libdivide_s64_gen等包裝函數(shù)來完成相同的操作。

簡單來說它幾乎可以平替項目中的除法運算，不過在這之前我們得先檢驗下它承諾的性能提升是不是確有其事。

libdivide在測試用例里自帶了一個性能測試程序，但這個程序的輸出比較抽象，測試的場景也不夠全面，因此我重新寫了三個場景的場景做測試。

三個場景分別是除數(shù)未知、除數(shù)已知但是2的冪以及除數(shù)已知但不是2的冪。覆蓋的情況是編譯器做不了優(yōu)化、編譯器可以優(yōu)化成位運算以及編譯器能優(yōu)化但不能直接用位運算進行替換這三種。

由于c++的編譯期計算太強大，為了避免編譯期計算攪局影響結(jié)果，測試數(shù)據(jù)中的大部分都是隨機生成的，理論上性能測試中應(yīng)該盡量減少這種隨機生成的數(shù)據(jù)，但這里我們別無他法，而且說到底也是“評估”一下庫的大致性能，不需要那么精確。測試用例不長，因此我就全搬上來了：

// 場景1，除數(shù)未知，為了模擬除數(shù)未知所以除數(shù)也用了隨機數(shù)
void bench_div(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    int64_t d = dis(gen);
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=d);
	    }
    }
}
BENCHMARK(bench_div);

void bench_libdiv(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    libdivide::divider<int64_t> fast_d(dis(gen));
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=fast_d);
	    }
    }
}
BENCHMARK(bench_libdiv);

// 場景2，除數(shù)的4，2的2次冪
void bench_div4(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<uint64_t> dis(1, 114515);
    std::vector<uint64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    uint64_t d = 4;
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n>>=d);
	    }
    }
}
BENCHMARK(bench_div4);

void bench_libdiv4(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<uint64_t> dis(1, 114515);
    std::vector<uint64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    uint64_t d = 4;
    libdivide::divider<uint64_t> fast_d(d);
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=fast_d);
	    }
    }
}
BENCHMARK(bench_libdiv4);

// 場景3，除數(shù)已知但不是2的冪，特地選了一個素數(shù)23
void bench_div_const(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    int64_t d = 23;
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=d);
	    }
    }
}
BENCHMARK(bench_div_const);

void bench_libdiv_const(benchmark::State &stat)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int64_t> dis(1, 114515);
    std::vector<int64_t> v;
    for (int i = 0; i < 10; ++i) {
	    v.push_back(dis(gen));
    }
    libdivide::divider<int64_t> fast_d(23);
    for (auto _ : stat) {
	    for (auto n : v) {
            benchmark::DoNotOptimize(n/=fast_d);
	    }
    }
}
BENCHMARK(bench_libdiv_const);

BENCHMARK_MAIN();

測試內(nèi)容是連續(xù)除十個隨機生成的被除數(shù)，現(xiàn)代cpu性能還是很強悍的，如果只測除一次的情況，那么會得到一堆0.X納秒的結(jié)果，那樣對比不夠明顯，也容易引入統(tǒng)計誤差和噪音。

測試運行也分兩部分，一是使用-O2優(yōu)化級別進行測試，在這個級別下編譯器會采用比較保守的優(yōu)化策略，并且只應(yīng)用少量的SIMD指令；另一個是用-O3 -march=native進行優(yōu)化，在這個級別下編譯器會最大限度優(yōu)化程序性能并且盡可能利用當(dāng)前cpu上所有可用的指令（包括SIMD）進行優(yōu)化。

先來看看老機器上(10代i5臺式機)的結(jié)果：

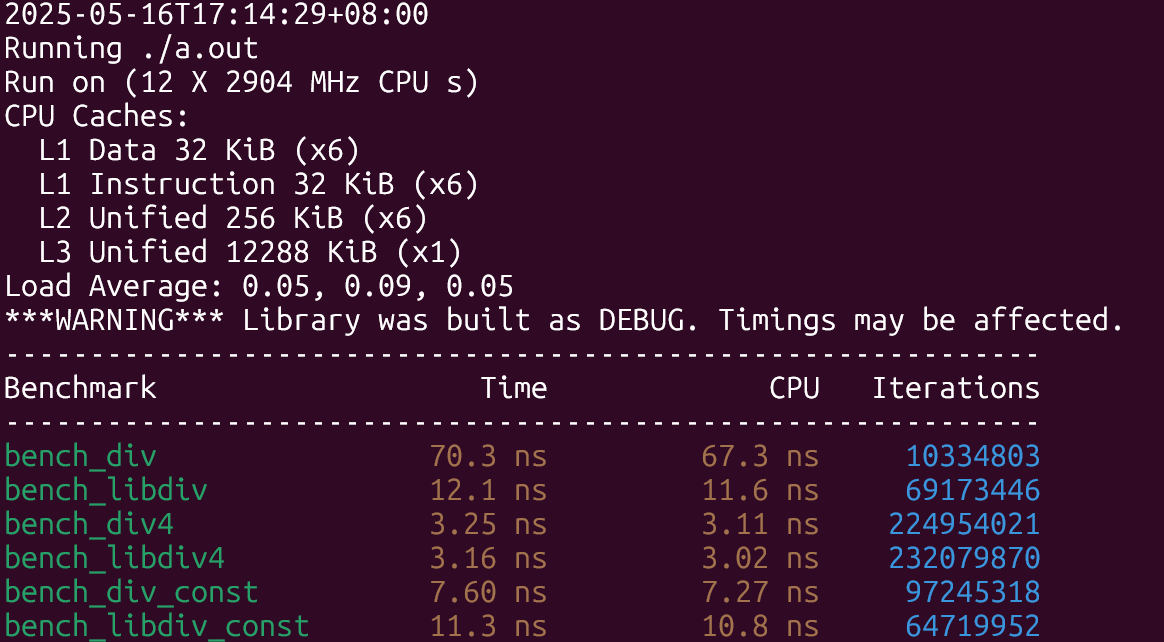
下面是開啟native之后的結(jié)果：

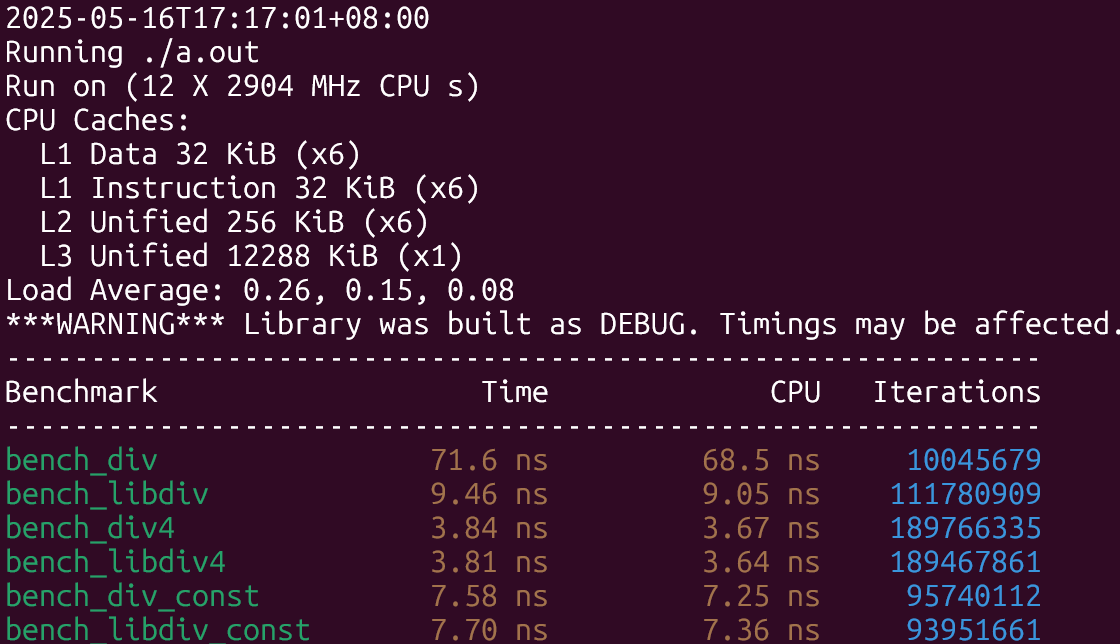
結(jié)果符合預(yù)期，在除數(shù)未知的情形下libdivide性能提升了8倍左右，除數(shù)已知且是2的冪的時候兩者差不多，只有第三種情形下libdivide稍慢與直接除，原因大概是因為編譯器也做了和libdivide類似的優(yōu)化，但libdivide還需要額外探測除數(shù)的性質(zhì)以及需要多幾次函數(shù)調(diào)用，因此性能上稍慢了一些。

最大化利用SIMD結(jié)果類似，情形3下的差距縮小了很多。

然后我們看看在更新的機器上的表現(xiàn)（14代i7）：

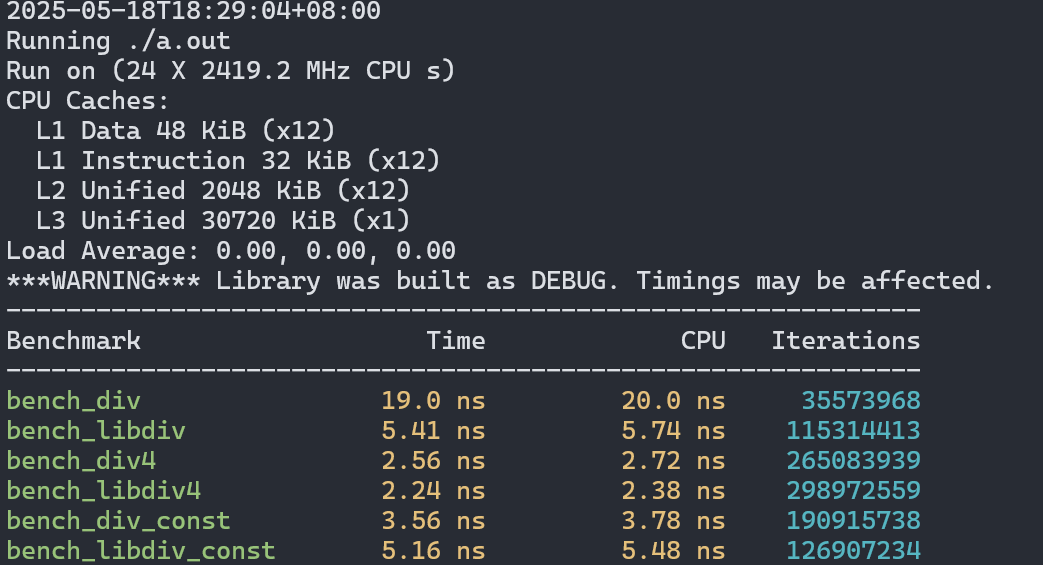
不啟用最高級別優(yōu)化時結(jié)果與老機器類似，但性能差距縮小了。

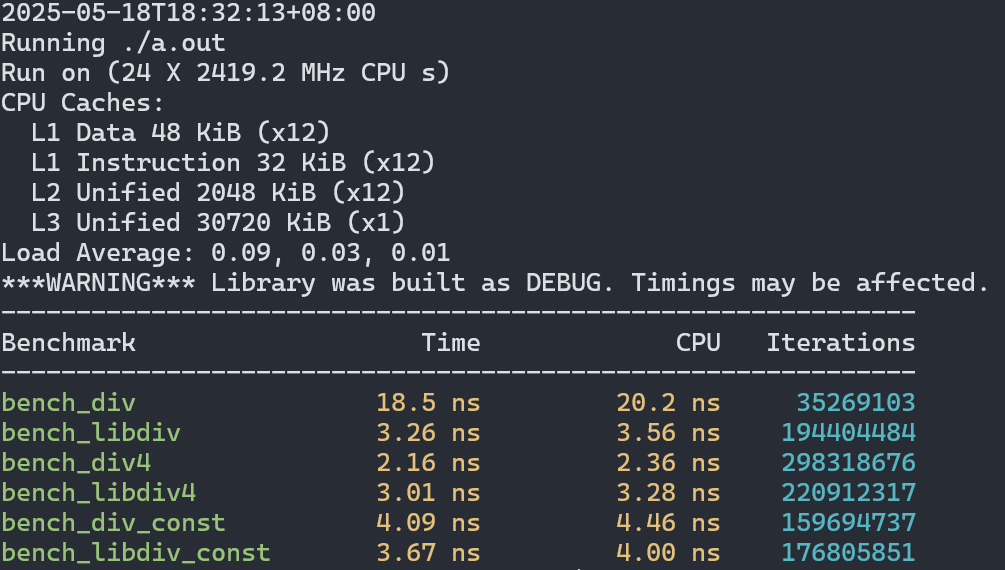
最大程度利用SIMD后現(xiàn)在情形3變快，但場景2又稍顯落后了。在場景1中的提升也只有5倍左右。

總體來說在libdivide宣稱的場景下，性能提升確實很可觀，但還沒到1個數(shù)量級這么夸張，不過我的測試環(huán)境都沒有avx512支持，對于支持這個指令集的cpu來說也許性能還能再提升一些最終達(dá)到文檔里說的10倍。在其他場景下libdivide的優(yōu)勢并不明顯，所以追求極致性能的時候不是很建議在非場景1的情況下使用這個庫。

總結(jié)

如果整數(shù)除法成為了性能瓶頸的話，可以嘗試使用libdivide。這里總結(jié)下優(yōu)缺點。

優(yōu)點：

1. 使用方便，只需要導(dǎo)入頭文件
2. 在除數(shù)未知的情況下能獲得顯著的性能提升
3. 能利用SIMD，充分釋放現(xiàn)代cpu性能

缺點：

1. 只適用于除數(shù)未知的情況下
2. 且除數(shù)要固定，因為頻繁創(chuàng)建銷毀libdivide::divider對象要付出額外的代價，會導(dǎo)致優(yōu)化效果打折甚至負(fù)優(yōu)化
3. libdivide::divider對象比整數(shù)要多占用一個字節(jié)，盡管這個對象是棧分配的，但對空間消耗比較敏感的程序可能需要謹(jǐn)慎使用，尤其是賬面是雖然只多一字節(jié)，但遇到需要內(nèi)存對齊的時候可能占用就要翻倍了。

總得來說libdivide還是很值得一試的庫，但任何優(yōu)化都要有性能測試做依據(jù)。