K 近鄰算法
K 近鄰算法(K-Nearest Neighbors,簡稱 KNN)是一種簡單且常用的分類和回歸算法。
K 近鄰算法屬于監督學習的一種,核心思想是通過計算待分類樣本與訓練集中各個樣本的距離,找到距離最近的 K 個樣本,然后根據這 K 個樣本的類別或值來預測待分類樣本的類別或值。
KNN 的基本原理
KNN 算法的基本原理可以概括為以下幾個步驟:
- 計算距離:計算待分類樣本與訓練集中每個樣本的距離。常用的距離度量方法有歐氏距離、曼哈頓距離等。
- 選擇 K 個最近鄰:根據計算出的距離,選擇距離最近的 K 個樣本。
- 投票或平均:對于分類問題,K 個最近鄰中出現次數最多的類別即為待分類樣本的類別;對于回歸問題,K 個最近鄰的值的平均值即為待分類樣本的值。
KNN 的特點
- 簡單易理解:KNN 算法的原理非常簡單,容易理解和實現。
- 無需訓練:KNN 是一種"懶惰學習"算法,不需要顯式的訓練過程,所有的計算都在預測時進行。
- 對數據分布無假設:KNN 不對數據的分布做任何假設,適用于各種類型的數據。
- 計算復雜度高:由于 KNN 需要在預測時計算所有樣本的距離,當數據集較大時,計算復雜度會很高。
KNN 算法的優缺點
優點
- 簡單易用:KNN 算法的原理簡單,易于理解和實現。
- 無需訓練:KNN 不需要顯式的訓練過程,所有的計算都在預測時進行。
- 適用于多分類問題:KNN 可以輕松處理多分類問題。
缺點
- 計算復雜度高:KNN 需要在預測時計算所有樣本的距離,當數據集較大時,計算復雜度會很高。
- 對噪聲敏感:KNN 對噪聲數據較為敏感,噪聲數據可能會影響預測結果。
- 需要選擇合適的 K 值:K 值的選擇對模型的性能有很大影響,選擇合適的 K 值是一個挑戰。
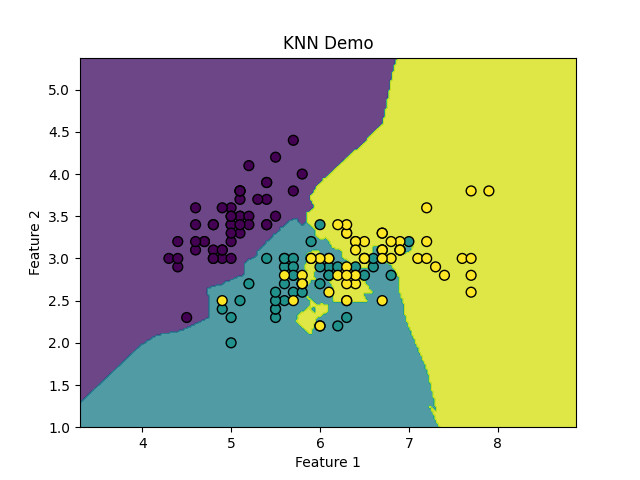
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score # 加載Iris數據集 iris = datasets.load_iris() X = iris.data[:, :2] # 只取前兩個特征,便于可視化 y = iris.target # 將數據集拆分為訓練集和測試集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 創建KNN模型,設置K值為3 knn = KNeighborsClassifier(n_neighbors=3) # 訓練模型 knn.fit(X_train, y_train) # 在測試集上進行預測 y_pred = knn.predict(X_test) # 計算準確率 accuracy = accuracy_score(y_test, y_pred) print(f"KNN模型的準確率: {accuracy:.4f}") # 繪制決策邊界和數據點 h = .02 # 網格步長 x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 # 創建一個二維網格,表示不同的樣本空間 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # 使用KNN模型預測網格中的每個點的類別 Z = knn.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) # 繪制決策邊界 plt.contourf(xx, yy, Z, alpha=0.8) # 繪制訓練數據點 plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50) plt.title("KNN Demo") plt.xlabel("Feature 1") plt.ylabel("Feature 2") plt.show()




 浙公網安備 33010602011771號
浙公網安備 33010602011771號